Файл: Отчет по лабораторной работе 2 исследование временных характеристик сау по дисциплине Основы теории управления.docx
Добавлен: 04.12.2023
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИCTEPCTBO НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное
образовательное учреждение высшего образования
«СЕВЕРО-КАВКАЗСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Кафедра инфокоммуникаций
Отчет по лабораторной работе №2
ИССЛЕДОВАНИЕ ВРЕМЕННЫХ ХАРАКТЕРИСТИК САУ
по дисциплине «Основы теории управления»
| Выполнил студент группы ИВТ-б-о-20-1 |
| Колбасов В.С. « »_________2022г. |
| Подпись студента___________ |
| Работа защищена « »____________2022г. |
| Проверил Линец Г.И. ________ (подпись) |
Ставрополь 2022
Цель: 1. Изучить динамические характеристики систем автоматического управления (САУ).
2. Приобрести навыки в получении и исследовании линейных динамических моделей с использованием пакета Control System Toolbox системы Matlab.
Вариант 9:
| 6 | –8 | –7 | 0 | –6 | –3 | –1 |
| b0 | b1 | a0 | a1 | a2 | a3 | a4 |
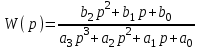
Ход работы:
-
Изучил теоретические сведения. -
Запустил систему MATLAB. -
Создал tf–объект, в соответствии с заданным вариантом.
Рисунок 1.
-
Используя комплексную передаточную функцию составил дифференциальное уравнение, определяющее функционирование САУ.
-
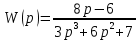
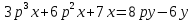
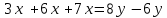
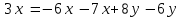
По дифференциальному уравнению построил структурную схему САУ.
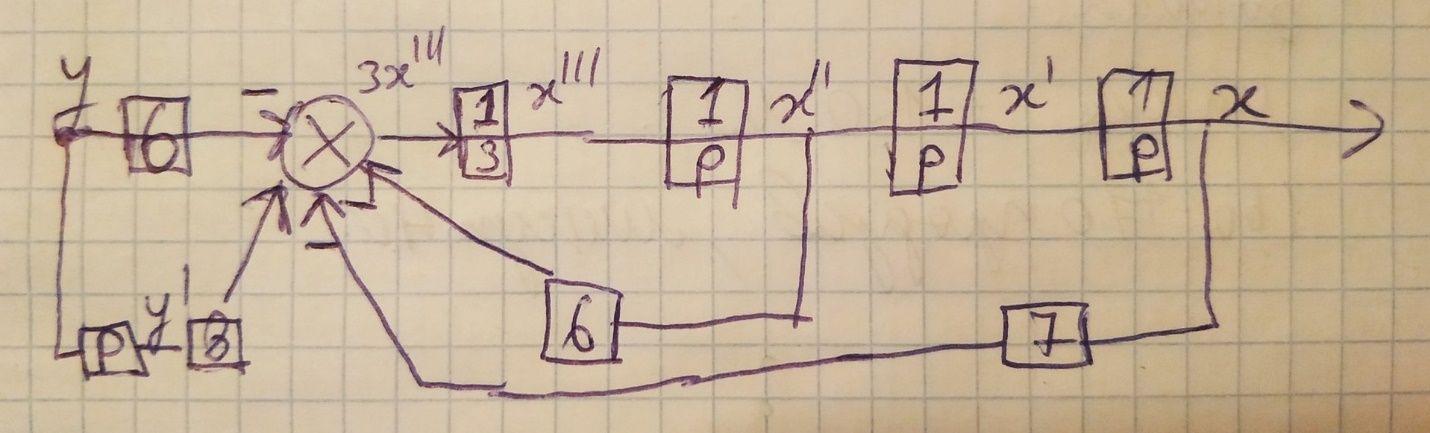
Рисунок 2
-
О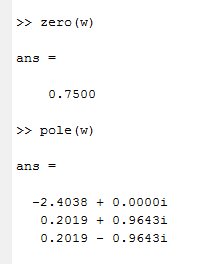
пределить полюса передаточной функции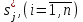
с использованием команды roots или pole. Определить нули передаточной функции 
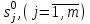с использованием команды roots или zero.
Рисунок 3
-
На комплексной плоскости получить расположение полюсов и нулей.
Р
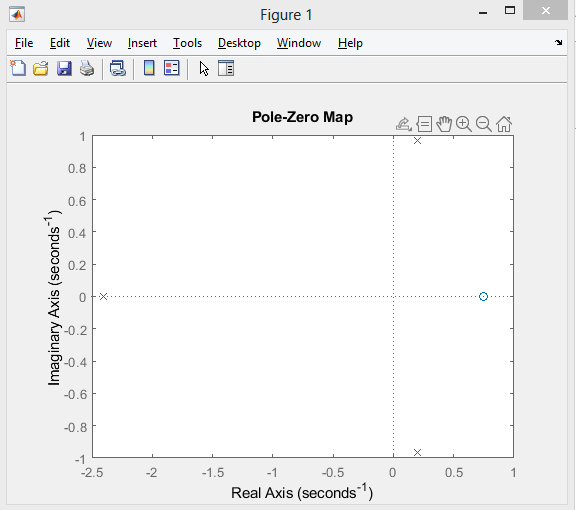
исунок 4
-
О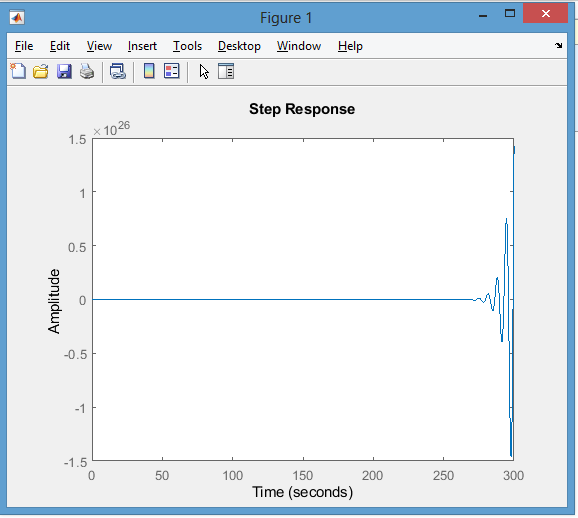
пределил переходную функцию, используя команду step(w).
Рисунок 5
-
П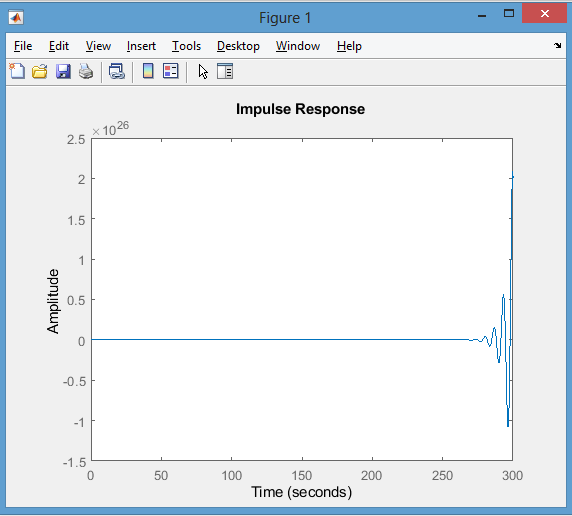
остроил импульсную переходную функцию, используя команду impulse(w).
Рисунок 6
-
В
ычислить коэффициент передачи, используя команду k=dcgain(w).
Рисунок 7
Контрольные вопросы
-
Как описываются непрерывные процессы, протекающие в системах управления?
Непрерывные процессы, протекающие в системах управления, могут быть описаны обыкновенными дифференциальными уравнениями с соответствующими начальными условиями. Тогда, если известен входной сигнал, выходной сигнал определяется в результате решения задачи Коши для обыкновенного дифференциального уравнения.
-
Представьте одномерную линейную непрерывную нестационарную и стационарную системы с помощью обыкновенных дифференциальных уравнений.
Одномерная линейная непрерывная нестационарная система управления описывается дифференциальным уравнением
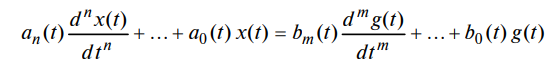
с начальными условиями
где g(t) – входной сигнал; x(t) – выходной сигнал; t – время; a
n(t),…,a0(t), bm(t),…,b0(t),– коэффициенты левой и правой частей уравнения; n и m – порядки старших производных выходного и входного сигналов соответственно; t0 – момент начала функционирования системы.
Если коэффициенты уравнения постоянны, система называется линейной стационарной:
-
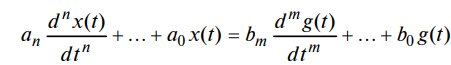
Как изображаются стационарные системы на структурных схемах?
Стационарные системы на структурных схемах изображаются следующим образом.
-
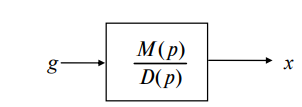
Дайте определение комплексной передаточной функции системы.
Передаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме.
-
Как определяются нули и полюса передаточной функции?
Передаточные функции содержат особые точки на комплексной плоскости -нули и полюса. Полюса - это те значения S, при которых передаточная функция превращается в бесконечность. Для определения полюсов необходимо собственный оператор (знаменатель передаточной функции) приравнять к нулю и произвести решение алгебраического уравнения относительно S. Нули - это те значения S, при которых передаточная функция равна нулю. Для нахождения нулей числитель передаточной функции приравнивается к нулю и полученное алгебраическое уравнение решается относительно S.
-
Дайте определение и поясните физический смысл переходной функции.
Реакция САУ на единичный скачок называется переходной функцией системы при нулевых начальных условиях и обозначается h(t).
Поясним физический смысл переходной функции. Переходная функция представляет собой переходный процесс на выходе системы, возникающий при подаче на ее вход скачкообразного воздействия единичной величины. Такое воздействие x(t) называется единичной ступенчатой функцией.
-
Дайте определение и поясните физический смысл импульсной переходной функции.
Если u(t) = d(t), то есть на вход системы поступает сигнал, определяемый функцией Дирака
, то реакция САУ на импульсное воздействие называется импульсной переходной функцией системы и обозначается w(t).
-
Каким образом связаны между собой переходная и импульсная переходная функции системы?
Импульсная переходная и переходная функции системы связаны следующим соотношением:
h(t)=∫f0w(τ)dτht=∫0fw????d????
-
Как описывается единичная функция с запаздыванием? Поясните ее физический смысл.
Для рассматриваемых линейных систем, т. е. для систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами, найдено, что простейшая форма изображения входной величины любого каскада представляется функциями вида
где параметр
представляет собой запаздывание, измеренное в секундах, а выражение F(s) является дробно-рациональной функцией от s.-
Приведите спектры амплитуды и фазы единичного ступенчатого сигнала. -
Какая существует связь между переходной и весовой функциями линейных звеньев?
Весовая и переходная функции являются исчерпывающими характеристиками систем автоматического управления при нулевых начальных условиях. По этим характеристикам можно однозначно определить выходную переменную системы при произвольном входном воздействии по формуле:
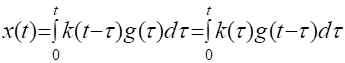
Вывод: в ходе выполнения лабораторной работы были изучены динамические характеристики систем автоматического управления (САУ). Также приобретены навыки в получении и исследовании линейных динамических моделей с использованием пакета Control System Toolbox системы Matlab.