Практическое занятиеНаименование занятия:Решение систем линейных уравнений методом ГауссаЦель занятия: Научиться решать системы линейных уравнений методом ГауссаРассмотрим произвольную систему линейных уравнений. Система m уравнений с n неизвестными в общем виде записывается следующим образом:где a_ij – коэффициенты, а b_i – постоянные. Решением системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Для этой системы линейных уравнений вида матрицаА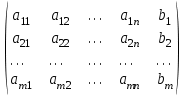^*= называется расширенной матрицей системыМетод ГауссаСуть метода заключается в том, что систему уравнений с помощью элементарных преобразований приводят к эквивалентной ей системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называются прямым ходом. Затем из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход). Элементарными преобразованиями систем являются:1) Умножение или деление коэффициентов и свободных членов на одно и то же число2) Сложение и вычитание уравнений3) Перестановка уравнений системы местами.4) Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулюПример. 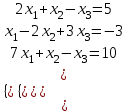Решить систему линейных уравнений методом Гаусса Составим расширенную матрицу системы.А* = 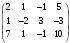. Выполним над этой матрицей следующие преобразования:

1. 
   поменяем местами 1 и 2 строки;
   
2. 
   прибавим к элементам 2 строки 1-ю строку, умноженную на -2;
   
3. 
   прибавим к элементам 3 строки 1-ю строку, умноженную на -7;
   
4. 
   прибавим к элементам 3 строки 2-ю строку, умноженную на -3;
   

---

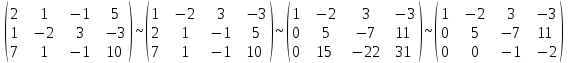
А* = Получили систему с треугольной матрицей. Таким образом, исходная система может быть представлена в виде: 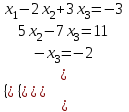, откуда получаем: x₃ = 2; x₂ = 5; x₁ = 1.

---

Смотрите также файлы

• Задание для самостоятельной работы к теме 1 Основы государственной политики в сфере воспитания. Базовые ценности российского общества.doc

• Решение о создании некоммерческой организации в результате ее учреждения принимается ее учредителями (учредителем). В отношении бюджетного или казенного учреждения такое решение принимается в порядке,.docx

• Молодёжная культура Интернет и социальные сети.docx

• 3блім. Бізді міріміздегі роботтар (орта таырыптар Таам жне сусын, Дені сауды жаны сау).docx

• Наследование.docx