Файл: Гидравликалы жне пневматикалы жйелер пні бойынша емтихан сратары.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. (3.2)
Барлық басқа көлденең ағыстар үшін (сонымен қатар ашық арналар үшін) Рейнольдс саны келесі формуламен анықталады:
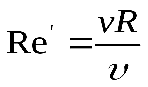немесе
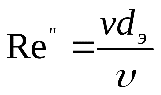, (3.3)
мұндағы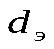
- эквивалентті (гидравликалық) диаметр, м.
Сұйықтық қозғалысының бірнеше түрін атауға болады: орныққан және орнықпаған; бірқалыпты және бірқалыпсыз; арынды және арынсыз.
Орныққан қозғалыс -уақыт өтуіне байланысты кез келген нүктедегі ағын жылдамдығы мен гидродинамикалық қысым өзгермей, ал тек қана сұйықтық ағынындағы қарастырылып отырған нүкте орнына тәуелді, яғни оның координаталарының функциясы болып табылатын сұйықтық қозғалысы.
Мысалы, тұрақты арындағы резервуар саңылауынан сұйықтықтың ағуы, каналдағы өзгермейтін көлденең қималы және тұрақты тереңдіктегі су ағыны.
Орнықпаған қозғалыс -уақыт өтуіне байланысты әр нүктедегі ағын жылдамдығы мен қысымы өзгеретін сұйықтық қозғалысы.
Мысалы, айнымалы арын кезінде резервуар саңылауынан сұйықтық ағуы.
Бірқалыпты қозғалыс -ұзындығы бойынша нақты ағыстар мен ағын жылдамдығы өзгермейтін сұйықтықтың орныққан қозғалысы.
Мысалы, өзгермейтін қималы және тұрақты тереңдіктегі құбыр немесе каналдағы сұйықтық қозғалысы.
Бірқалыпсыз қозғалыс -ұзындығы бойынша нақты ағыстар мен ағын жылдамдығы өзгеретін сұйықтықтың орныққан қозғалысы.
Мысалы, конустық құбырда және табиғи арнадағы сұйықтықтың қозғалысы.
Арынды қозғалыс -құбыр өткізгіштің барлық көлденең қимасы атмосфералықтан жоғары қысыммен толтырылатын сұйықтық қозғалысы: сұйықтық қозғалысы қысым күштері арқасында жүзеге асады, яғни қосымша энергия шығынын тудырытын арын арқасында.
Арынсыз қозғалыс -атмосфералық қысымның астында орналасқан бос беті бар ағындағы сұйықтық қозғалысы.
Ағын режимі: Ламинарлы, Турбулентті
Ағын шығыны Q - t бірлік уақыт аралығында ω тірі қима арқылы өтетін V сұйықтықтың көлемі: Q=V/t,м^3/с
Ағынның орташа жылдамдығы υ – Q сұйықтық шығынының ω тірі қима ауданына қатынасымен анықталатын сұйықтықтың қозғалу жылдамдығы:
ϑ_орт=Q/ω,м/с
Ағынның гидравликалық радиусы R – тірі қиманың сулану (жұғу) периметріне қатынасы: R=ω/χ, м
Ағу сызығы (орнықпаған қозғалыс кезінде қолданылады) бұл әрбір нүктесінде берілген уақыт мезетіндегі жылдамдық векторы жанама бойынша бағытталған қисық.
Ағу түтігі – көлденең қимасы шексіз аз ағу сызықтары түзетін түтікшелі бет. Ағу түтігінің ішінде орналасқан ағын бөлігі элементар ағынша деп аталады.
1738 ж. Алынған Даниил Бернуллидің теңдеуі гидродинамиканың негізгі теңдеуі болып табылады. Ол ағынның әртүрлі қималарындағы қысым P, орташа жылдамдық υ пен пьезометрлік биіктік z арасындағы байланысты көрсетеді және қозғалыстағы сұйықтықтың энергиясының сақталу заңын өрнектейді. Осы теңдеудің көмегімен көптеген есептер шешіледі.
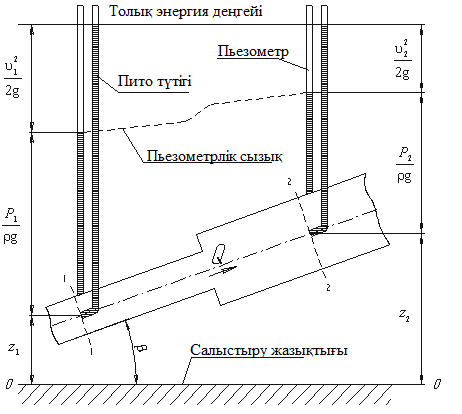
Егер Пито түтігіндегі сұйықтық деңгейлерінің көрсеткіші арқылы түзу жүргізсе, ол көлденең болады және құбыр өткізгіштің толық энергиясының деңгейін көрсететін болады.
Идеал сұйықтық ағынындағы ерікті таңдап алынған екі 1-1 және 2-2 қималары үшін Бернулли теңдеуі келесі түрде болады:
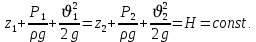
1-1және2-2 қималары еркімізше таңдап алынғандықтан, онда алынған теңдеуді басқаша жазуға болады:
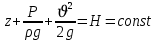
және былайша оқуға болады: идеал сұйықтық ағынының кез келген қимасы үшін Бернулли теңдеуінің үш мүшесінің қосындысы тұрақты шама болып табылады.
Энергетикалық тұрғыдан алып қарағанда теңдеудің әрбір мүшесі белгілі бір энергияның түрін білдіреді:
z1 және z2 - 1-1 және 2-2 қималарындағы потенциалдық энергияны сипаттайтын меншікті орналасу энергиясы;
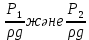- дәл осы қималардағы қысымның потенциалдық энергиясын сипаттайтын меншікті қысым энергиясы;
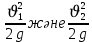- дәл осы қималардағы меншікті кинетикалық энергиялар.
Осыдан шығатыны, Бернулли теңдеуіне сәйкес кез келген қимадағы идеал сұйықтықтың толық меншікті энергиясы тұрақты.
Бернулли теңдеуін таза геометриялық тұрғыдан да түсіндіруге болады. Оның мәнісі теңдеудің әрбір мүшесінің сызықтық өлшемдері бар екендігінде. 3.5-суретке қарай отырып, z
1 және z2 - 1-1 және 2-2 қималарының салыстырмалы жазықтықтан геометриялық биіктігі екенін;
-пьезометрлік биіктіктер екенін; 
- көрсетілген қималардағы жылдамдық биіктіктері екенін көруге болады. Бұл жағдайда Бернулли теңдеуін былайша тұжырымдауға болады: идеал сұйықтық үшін геометриялық, пьезометрлік және жылдамдық биіктіктерінің қосындысы тұрақты шама.
Бернулли теңдеуі қозғалыстағы сұйықтың жылдамдығын,гидродинамикалық қысымын,ауырлық центрлерінің биіктік нүктерелерін z өзара байланыстыратын гидродинамиканың негізгі теңдеуі болып табылады.
Сұйықтықтың идеал ағыншасына қарағанда ішкі және сыртқы үйкеліс күштері ескеріледі де,соған сәйкес,ол осы күштерді жеңуге кететін энергия азаюмен ерекшеленеді.Энергияның бұл азаюларын арын азаюы деп атайды.
Әр түрлі кедергілерді жеңуге кететін механикалық энергия жойылып кетпей,жылулық энергияға түрленеді.Сөйтіп,энергияның сақталу заңы нақты сұйық үшін де өз күшінде қалады.
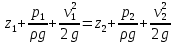
Нақты сұйықтықтың ағынына арналған Бернулли теңдеуі
Бернулли теңдеуі құбырлардағы, арналардағы және басқа объектілердегі сұйықтықтың немесе газдың қозғалысын сипаттайтын гидродинамиканың негізгі теориялық негізі болып табылады. Бұл теңдеу кез-келген қимадағы сұйықтықтың немесе газдың қысымының, потенциалдық және кинетикалық энергиясының қосындысы ағын бойында тұрақты болуы керек екенін анықтайды.
Нақты сұйықтықтар үшін Бернулли теңдеуі құбырлар мен арналар ішіндегі қарсылық күштерін, сондай-ақ ағынның турбуленттілігіне байланысты энергия шығынын тудыратын сұйықтықтың ішкі үйкелісінен энергия шығынын ескеру үшін өзгертіледі.
Нақты сұйықтықтар ағыны үшін Бернулли теңдеуі:
теңдігінен біршама өзгешелеу болып табылады. Оның мәнісі нақты тұтқыр сұйықтықтың қозғалысы кезінде сұйықтық жеңу үшін энергия жұмсайтын үйкеліс күштері пайда болады.
Жоғалған энергия немесе жоғалған арын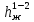
деп белгіленеді және ол да сызықтық өлшемге ие болады.
Нақты сұйықтықтар үшін Бернулли теңдеуі келесі түрде болады:
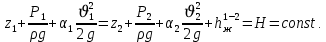(3.14)
Гидродинамикаға қатысты есептерді шешу үшін Бернулли теңдеуі ең көп қолданылатын құралдардың бірі болып табылады. Оны жүйенің кез келген нүктесіндегі сұйықтықтың жылдамдығын немесе қысымын анықтау үшін, сондай-ақ сұйықтықты тасымалдау процесінде энергия шығынын есептеу үшін пайдалануға болады.
Нақты сұйықтықтың ағуы белгілі бір шарттарға байланысты бір түрінен екінші түріне ауыса алатын әр түрлі режимдердің қозғалысымен сипатталады.
Гидравликалық кедергілердің экспериментті зерттеулері арын жоғалтулардың (энергия жоғалтулар) ағындағы қозғалыстың режиміне тәуелді екендігін көрсетеді.
Әр түрлі физикалық қасиеттерге ие сұйықтықтардың ағуын зерттей келе Рейнольдс қозғалыс ламинарлы және турбулентті болады деп бекітті.
«Ламинарлы» латынның lamina сөзінен шыққан – қабат. Ламинарлы режим деп сұйықтықтың ағын бойымен қабат-қабат болып бір-бірімен араласпай ағуын айтамыз. Тәжірибеде ламинарлы режим тұтқырлығы жоғары сұйықтықтарда (мұнай, жақпа майлары) және жіңішке құбырлар мен құбыржолдарда су ағынының жылдамдығы төмен болғанда кездеседі.
«Турбулентті» латынның turbulentus сөзінен шыққан – ретсіз. Турбулентті режим деп ағын ағысының бұзылып барлық қабаттардың араласып ағуын айтамыз. Тәжірибеде турбулентті режим көбінесе сұйықтық қозғалысында кездеседі.
Бір режимнен келесі режимге ауысу ағыс жыламдығының V құбыр диаметрімен d және сұйықтықтың кинематикалық тығыздығымен ν белгілі бір қатынасқа түскенде орындалады. Бұл өлшемсіз қатынас Рейнольдстің ауытқымалы саны деп аталып, мына формуламен анықталады
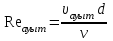
Ағыстың ламинарлы режимінің бар болуының шарты мына теңсіздік болып табылады: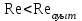
, яғни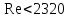 
Бұл дегеніміз ламинарлы режим әдетте жылдамдығы төмен, құбырының диаметрі аз немесе тұтқырлығы жоғары жерлердегі Рейнольдс санының аз шамасында (2320-ге дейін) кездеседі.
Re санының диапазоны 2320 бен 4000 арасында болса, ол ламинарлы режим мен турбулентті режимнің арасындағы ауыспалы аймақ немесе толық дамымаған турбулентті режим деп аталады.
Re > 4000 болған жағдайда ағыс режимі турбулентті деп есептеледі.
Жергілікті гидравликалық кедергілердегі арын азаюын Вейсбах формуласы бойынша анықтайды
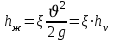
Мұнда ξ (дзета) – жергілікті кедергі коэффициенті
Жергілікті кедергі коэффициентін табу үшін жергілікті кедергіге дейінгі және одан кейінгі сұйықтың толық арынын Н1 және Н2 өлшеп, олардың айырмасын жылдамдықтық арынға hv бөлу керек.
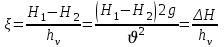
Жергілікті кедергі коэффициентінің ξ мәндері
Барлық басқа көлденең ағыстар үшін (сонымен қатар ашық арналар үшін) Рейнольдс саны келесі формуламен анықталады:
немесе , (3.3)мұндағы
- эквивалентті (гидравликалық) диаметр, м.Сұйықтық қозғалысының бірнеше түрін атауға болады: орныққан және орнықпаған; бірқалыпты және бірқалыпсыз; арынды және арынсыз.
Орныққан қозғалыс -уақыт өтуіне байланысты кез келген нүктедегі ағын жылдамдығы мен гидродинамикалық қысым өзгермей, ал тек қана сұйықтық ағынындағы қарастырылып отырған нүкте орнына тәуелді, яғни оның координаталарының функциясы болып табылатын сұйықтық қозғалысы.
Мысалы, тұрақты арындағы резервуар саңылауынан сұйықтықтың ағуы, каналдағы өзгермейтін көлденең қималы және тұрақты тереңдіктегі су ағыны.
Орнықпаған қозғалыс -уақыт өтуіне байланысты әр нүктедегі ағын жылдамдығы мен қысымы өзгеретін сұйықтық қозғалысы.
Мысалы, айнымалы арын кезінде резервуар саңылауынан сұйықтық ағуы.
Бірқалыпты қозғалыс -ұзындығы бойынша нақты ағыстар мен ағын жылдамдығы өзгермейтін сұйықтықтың орныққан қозғалысы.
Мысалы, өзгермейтін қималы және тұрақты тереңдіктегі құбыр немесе каналдағы сұйықтық қозғалысы.
Бірқалыпсыз қозғалыс -ұзындығы бойынша нақты ағыстар мен ағын жылдамдығы өзгеретін сұйықтықтың орныққан қозғалысы.
Мысалы, конустық құбырда және табиғи арнадағы сұйықтықтың қозғалысы.
Арынды қозғалыс -құбыр өткізгіштің барлық көлденең қимасы атмосфералықтан жоғары қысыммен толтырылатын сұйықтық қозғалысы: сұйықтық қозғалысы қысым күштері арқасында жүзеге асады, яғни қосымша энергия шығынын тудырытын арын арқасында.
Арынсыз қозғалыс -атмосфералық қысымның астында орналасқан бос беті бар ағындағы сұйықтық қозғалысы.
-
Ағынның гидравликалық сипаттамалары
Ағын режимі: Ламинарлы, Турбулентті
Ағын шығыны Q - t бірлік уақыт аралығында ω тірі қима арқылы өтетін V сұйықтықтың көлемі: Q=V/t,м^3/с
Ағынның орташа жылдамдығы υ – Q сұйықтық шығынының ω тірі қима ауданына қатынасымен анықталатын сұйықтықтың қозғалу жылдамдығы:
ϑ_орт=Q/ω,м/с
Ағынның гидравликалық радиусы R – тірі қиманың сулану (жұғу) периметріне қатынасы: R=ω/χ, м
Ағу сызығы (орнықпаған қозғалыс кезінде қолданылады) бұл әрбір нүктесінде берілген уақыт мезетіндегі жылдамдық векторы жанама бойынша бағытталған қисық.
Ағу түтігі – көлденең қимасы шексіз аз ағу сызықтары түзетін түтікшелі бет. Ағу түтігінің ішінде орналасқан ағын бөлігі элементар ағынша деп аталады.
-
Идеал сұйықтыққа арналған Бернулли теңдеуі
1738 ж. Алынған Даниил Бернуллидің теңдеуі гидродинамиканың негізгі теңдеуі болып табылады. Ол ағынның әртүрлі қималарындағы қысым P, орташа жылдамдық υ пен пьезометрлік биіктік z арасындағы байланысты көрсетеді және қозғалыстағы сұйықтықтың энергиясының сақталу заңын өрнектейді. Осы теңдеудің көмегімен көптеген есептер шешіледі.
Егер Пито түтігіндегі сұйықтық деңгейлерінің көрсеткіші арқылы түзу жүргізсе, ол көлденең болады және құбыр өткізгіштің толық энергиясының деңгейін көрсететін болады.
Идеал сұйықтық ағынындағы ерікті таңдап алынған екі 1-1 және 2-2 қималары үшін Бернулли теңдеуі келесі түрде болады:
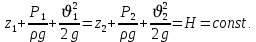
1-1және2-2 қималары еркімізше таңдап алынғандықтан, онда алынған теңдеуді басқаша жазуға болады:
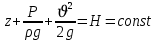
және былайша оқуға болады: идеал сұйықтық ағынының кез келген қимасы үшін Бернулли теңдеуінің үш мүшесінің қосындысы тұрақты шама болып табылады.
Энергетикалық тұрғыдан алып қарағанда теңдеудің әрбір мүшесі белгілі бір энергияның түрін білдіреді:
z1 және z2 - 1-1 және 2-2 қималарындағы потенциалдық энергияны сипаттайтын меншікті орналасу энергиясы;
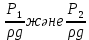- дәл осы қималардағы қысымның потенциалдық энергиясын сипаттайтын меншікті қысым энергиясы; 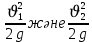- дәл осы қималардағы меншікті кинетикалық энергиялар. Осыдан шығатыны, Бернулли теңдеуіне сәйкес кез келген қимадағы идеал сұйықтықтың толық меншікті энергиясы тұрақты.
Бернулли теңдеуін таза геометриялық тұрғыдан да түсіндіруге болады. Оның мәнісі теңдеудің әрбір мүшесінің сызықтық өлшемдері бар екендігінде. 3.5-суретке қарай отырып, z
1 және z2 - 1-1 және 2-2 қималарының салыстырмалы жазықтықтан геометриялық биіктігі екенін;
-пьезометрлік биіктіктер екенін; - көрсетілген қималардағы жылдамдық биіктіктері екенін көруге болады. Бұл жағдайда Бернулли теңдеуін былайша тұжырымдауға болады: идеал сұйықтық үшін геометриялық, пьезометрлік және жылдамдық биіктіктерінің қосындысы тұрақты шама. -
Нақты сұйықтықтың ағыншасына арналған Бернулли теңдеуі
Бернулли теңдеуі қозғалыстағы сұйықтың жылдамдығын,гидродинамикалық қысымын,ауырлық центрлерінің биіктік нүктерелерін z өзара байланыстыратын гидродинамиканың негізгі теңдеуі болып табылады.
Сұйықтықтың идеал ағыншасына қарағанда ішкі және сыртқы үйкеліс күштері ескеріледі де,соған сәйкес,ол осы күштерді жеңуге кететін энергия азаюмен ерекшеленеді.Энергияның бұл азаюларын арын азаюы деп атайды.
Әр түрлі кедергілерді жеңуге кететін механикалық энергия жойылып кетпей,жылулық энергияға түрленеді.Сөйтіп,энергияның сақталу заңы нақты сұйық үшін де өз күшінде қалады.
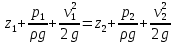
- 1 2 3
Нақты сұйықтықтың ағынына арналған Бернулли теңдеуі
Бернулли теңдеуі құбырлардағы, арналардағы және басқа объектілердегі сұйықтықтың немесе газдың қозғалысын сипаттайтын гидродинамиканың негізгі теориялық негізі болып табылады. Бұл теңдеу кез-келген қимадағы сұйықтықтың немесе газдың қысымының, потенциалдық және кинетикалық энергиясының қосындысы ағын бойында тұрақты болуы керек екенін анықтайды.
Нақты сұйықтықтар үшін Бернулли теңдеуі құбырлар мен арналар ішіндегі қарсылық күштерін, сондай-ақ ағынның турбуленттілігіне байланысты энергия шығынын тудыратын сұйықтықтың ішкі үйкелісінен энергия шығынын ескеру үшін өзгертіледі.
Нақты сұйықтықтар ағыны үшін Бернулли теңдеуі:
теңдігінен біршама өзгешелеу болып табылады. Оның мәнісі нақты тұтқыр сұйықтықтың қозғалысы кезінде сұйықтық жеңу үшін энергия жұмсайтын үйкеліс күштері пайда болады.
Жоғалған энергия немесе жоғалған арын
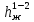деп белгіленеді және ол да сызықтық өлшемге ие болады.Нақты сұйықтықтар үшін Бернулли теңдеуі келесі түрде болады:
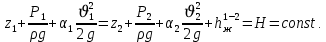(3.14)Гидродинамикаға қатысты есептерді шешу үшін Бернулли теңдеуі ең көп қолданылатын құралдардың бірі болып табылады. Оны жүйенің кез келген нүктесіндегі сұйықтықтың жылдамдығын немесе қысымын анықтау үшін, сондай-ақ сұйықтықты тасымалдау процесінде энергия шығынын есептеу үшін пайдалануға болады.
-
Нақты сұйықтықтың қозғалу режимдері
Нақты сұйықтықтың ағуы белгілі бір шарттарға байланысты бір түрінен екінші түріне ауыса алатын әр түрлі режимдердің қозғалысымен сипатталады.
Гидравликалық кедергілердің экспериментті зерттеулері арын жоғалтулардың (энергия жоғалтулар) ағындағы қозғалыстың режиміне тәуелді екендігін көрсетеді.
Әр түрлі физикалық қасиеттерге ие сұйықтықтардың ағуын зерттей келе Рейнольдс қозғалыс ламинарлы және турбулентті болады деп бекітті.
«Ламинарлы» латынның lamina сөзінен шыққан – қабат. Ламинарлы режим деп сұйықтықтың ағын бойымен қабат-қабат болып бір-бірімен араласпай ағуын айтамыз. Тәжірибеде ламинарлы режим тұтқырлығы жоғары сұйықтықтарда (мұнай, жақпа майлары) және жіңішке құбырлар мен құбыржолдарда су ағынының жылдамдығы төмен болғанда кездеседі.
«Турбулентті» латынның turbulentus сөзінен шыққан – ретсіз. Турбулентті режим деп ағын ағысының бұзылып барлық қабаттардың араласып ағуын айтамыз. Тәжірибеде турбулентті режим көбінесе сұйықтық қозғалысында кездеседі.
Бір режимнен келесі режимге ауысу ағыс жыламдығының V құбыр диаметрімен d және сұйықтықтың кинематикалық тығыздығымен ν белгілі бір қатынасқа түскенде орындалады. Бұл өлшемсіз қатынас Рейнольдстің ауытқымалы саны деп аталып, мына формуламен анықталады
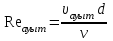
Ағыстың ламинарлы режимінің бар болуының шарты мына теңсіздік болып табылады:
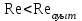, яғни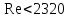 Бұл дегеніміз ламинарлы режим әдетте жылдамдығы төмен, құбырының диаметрі аз немесе тұтқырлығы жоғары жерлердегі Рейнольдс санының аз шамасында (2320-ге дейін) кездеседі.
Re санының диапазоны 2320 бен 4000 арасында болса, ол ламинарлы режим мен турбулентті режимнің арасындағы ауыспалы аймақ немесе толық дамымаған турбулентті режим деп аталады.
Re > 4000 болған жағдайда ағыс режимі турбулентті деп есептеледі.
-
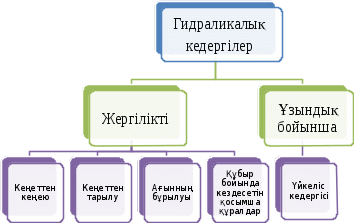
Жергілікті және ұзындық бойынша гидравликалық кедергілер
Жергілікті гидравликалық кедергілердегі арын азаюын Вейсбах формуласы бойынша анықтайды
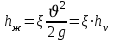
Мұнда ξ (дзета) – жергілікті кедергі коэффициенті
Жергілікті кедергі коэффициентін табу үшін жергілікті кедергіге дейінгі және одан кейінгі сұйықтың толық арынын Н1 және Н2 өлшеп, олардың айырмасын жылдамдықтық арынға hv бөлу керек.
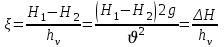
Жергілікті кедергі коэффициентінің ξ мәндері
| Кедергі түрлері | ξ коэффициентінің мәні |
| Құбырға ену | 0,5 |
| Кенеттен тарылу |  |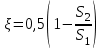
| Кенеттен кеңею |  |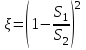
| Құбырдан шығу | 1 |