Бланк выполнения задания 1. Вариант 1.3
Тема 5. Короткие замыкания в системах электроснабжения

Задание:

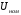- Выполнить проверку кабеля с бумажно-масляной изоляцией сечением на напряжение , на термическую стойкость току короткого замыкания 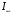, если время действия тока КЗ .

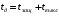- Определить температуру проводника в момент отключения тока КЗ.

- Если заданный кабель не прошел проверку по термической стойкости к току КЗ, разработайть предложения по сохранению в работе кабеля заданного сечения.

Вводные данные:

Вариант	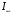, А	Uном, кВ	tзащ, с	tзвыкл, с	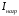, А	s, мм2
13	6000	6	0,35	0,12		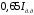3×35

Таблица 1.1

Допустимые температуры токоведущих жил медных проводников

для кабелей с бумажно-масляной изоляцией

Характеристики проводника	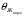, °С	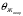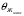, °С	, °С	Значения С,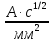
Uном = 6 кВ	65	100	200	145

---

Таблица 1.2

Длительно допустимый ток для трехжильных кабелей с медными жилами и бумажно-масляной изоляцией

Сечение токопроводящей жилы, s, мм2	Длительно допустимый ток, Iд.д, А
	до 3 кВ	6 кВ	10 кВ
35	190	160	150

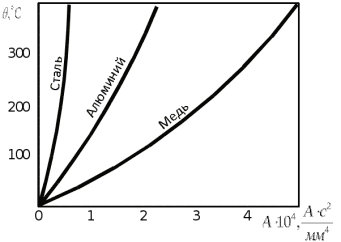
Рис. 1. Кривые нагрева токоведущих частей, изготовленных из различных материалов

Выполнение задания:

Для медного кабеля 3х35 длительно допустимы ток 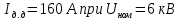и допустимая температура .

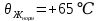Определим температуру нагрева кабеля в нормальном режиме при протекании тока нагрузки 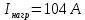без учета температуры окружающей среды по формуле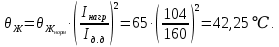



Найденному значению температуры жилы кабеля в нормльном режиме работы по графику на рисунке 1 соответствует начальное значение интеграла квадратичной плотности тока .

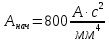Расчетное приведенное время действия короткого замыкания найдем по формуле



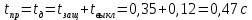
Значение интеграла квадратичной плотности тока, рмо пропорционального количеству тепла, выделяемого в проводнике при коротком замыкании, определим по формуле



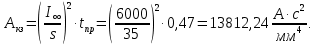
Используя ранее определенные значения интеграла квадратичной плотности тока 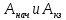, найдем знаачение ,

---

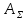которое прямо пропорционально количеству тепла, выделяемого в проводнике после короткого замыкания



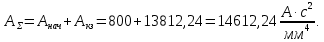
По графику, представленному на рисунке 1, определим соответствующую температуру – 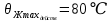. Макимально допустимая температура жил .

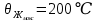Выполним проверку сечения кабеля на термическую стойкость току короткого замыкания по формуле



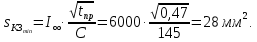
Сравнивая значение минимального сечения кабеля 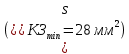с заданным по условию задачи 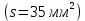, делаем вывод, что данный кабель подходит для использования.

Определим наибольшее приведенное значение времени действия тока короткого замыкания, которое будет удовлетворять условию термической стойкости заданного сечения по формле



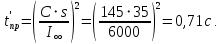
Проверим значение температуры жил кабеля при наибольшем значении приведенного времени дйствия короткого заыкания по формуле



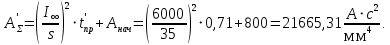
По графику, представленному на рисунке 1, для значения 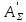значение температуры 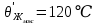, что не превышает максимально допустимого значения 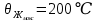. Следовательно, экссплуатация кабеля с заданным сечением возможна.

---

Смотрите также файлы

• Классный час, посвященный 75летию Алтайского края я алтай Россия. 2 класс Петрова Людмила Артуровна.docx

• Суммативное оценивание за раздел формулы сокращенного умножения.doc

• Ответы на вопросы Каковы основные этапы становления классицизма во Франции и особенности каждого из них.docx

• Инструкция к выполнению Внимательно прочитайте задание.docx

• Ю. В. Данник Руководитель направления.pdf