Файл: Моделирование нечетких систем средствами нечеткой логики в matlab.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 15
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Моделирование нечетких систем средствами нечеткой логики в matlab
Моделирование нечетких систем средствами нечеткой логики в matlab
Моделирование нечетких систем средствами нечеткой логики в matlab
Моделирование нечетких систем средствами нечеткой логики в matlab
Моделирование нечетких систем средствами нечеткой логики в matlab
В составе Matlab присутствуют пять основных средств графического интерфейса пользователя (ГИП), которые обеспечивают доступ к ИНЛ: редакторы системы нечеткого вывода (СНВ), функции принадлежности, правил вывода, а также средства просмотра правил и поверхности вывода. Эти средства связаны между собой динамически и производимые изменения в одном из них влекут изменения в других. Редактор СНВ предоставляет возможность формирования проектируемой системы на высоком уровне абстракции: количество входных и выходных переменных, наименование переменных. Редактор функций принадлежности (ФП) используется для определения формы ФП, ассоциированных с каждой переменной. Редактор правил вывода применяется для редактирования списка правил, которые определяют поведение проектируемой системы. Средство просмотра правил вывода используется в целях диагностики и может показывать, например, активность правил или форму влияния отдельных ФП на результат нечеткого вывода. Средство просмотра поверхности вывода используется для отображения зависимости выхода системы от одного или двух входов. Другими словами, оно генерирует и выводит карту поверхности вывода разработанной СНВ. Редактор СНВ. Построение нечетких систем по Мамдани. Для построения создаваемой системы в командной строке основного окна Matlabнеобходимо набрать команду fuzzy. Окно редактора новой СНВ содержит входную, обозначенную input1 и выходную — output1 переменные. По умолчанию ИНЛ предлагает создавать СНВ типа Мамдани. Для того чтобы добавить новую переменную, необходимо выбрать в меню Editсоответствующий пункт (для входной переменной – Addinput, для выходной – Addoutput). Изменение наименования переменной происходит по шагам. Шаг 1. Отмечается переменная, которую необходимо переименовать. Шаг 2. В поле редактирования изменяется наименование переменной по умолчанию на имя, предложенное пользователем. Сохранение проектируемой системы в рабочее пространство среды MATLAB (в переменную) производится с помощью пункта меню File– Savetoworkspaceas... В этом случае данные сохраняются до окончания сеанса работы с Matlab. Для сохранения данных на диске после окончания сеанса работы применяется соответствующий пункт того же меню – Savetodiskas... Редактор ФП. Следующим шагом в построении нечеткой модели средствами ИНЛ является ассоциирование набора ФП с каждой входной и выходной переменной. Данная операция производится в редакторе ФП тремя способами, активизировать который можно:
С помощью редактора ФП можно отображать и редактировать любые ФП, ассоциированные (связанные) со всеми входными и выходными переменными разрабатываемой СНВ. Связывание ФП с именем переменной происходит следующим образом:
Редактируют ФП текущей переменной двумя способами: используя графическое окно ФП или изменяя характеристики ФП (наименование, тип и числовые параметры). При выборе необходимой ФП в графическом окне допускается плавное изменение кривой с помощью мыши. Таким образом, при построении СНВ необходимо с помощью редактора ФП определить соответствующие функции для каждой из входных и выходных переменных. Редактор правил вывода После того как указано количество входных и выходных переменных, определены их наименования и построены соответствующие ФП, в СНВ необходимо включить правила вывода. Для этого в меню View выбирается пункт EditRules... или в командной строке Matlabнабирается команда ruleedit. Основываясь на описаниях входных и выходных переменных, определенных в редакторе ФП, редактор правил вывода формирует структуру правила автоматически. От пользователя требуется лишь связать значения входных и выходных переменных, выбирая из списка заданных ранее ФП и определить логические связки между ними. Также допускается использование логического отрицания (НЕ) и изменение весов правил в диапазоне от 0 до 1. Правила вывода могут отображаться в окне в различных форматах, которые определяются путем выбора соответствующего пункта подменю Format меню Options. По умолчанию используется расширенный формат отображения правил вывода (verbose form): If (input_1 is[not] mf_1j1) (input_n is[not] mf__njn) then (output_1 is[not] mf_n + 1jn+1) (output_k is[not] mf_k + njk+n) где i – номер входной переменной; ji – номер ФП i-й переменной; k – номер выходной переменной; n – количество входных переменных; т –количество выходных переменных; w – вес правила. (Круглые скобки заключают в себе обязательные параметры, квадратные – необязательные, а угловые – альтернативные параметры (один на выбор)). Кроме формата по умолчанию, существуют еще два вида форматов отображения правил: символьный (symbolic form) и индексный (indexed form). Символьный формат имеет следующий вид: (input_1<=,==>mf_1j1)<&, | >... (input_i<=,==>mf_iji)…<&, | > (input_n<=,==>mf_njn)=> (output_1<=,==>mf_n + 1jn+1)...<&, | > (output_k<=,==>mf_k + njk+n) <&, | >... (output_m<=,==>mf_m + njm не равно n) (W) Отличие символьного формата от расширенного состоит в том, что вместо словесной интерпретации связок используется символьная (символы «&» и «|» – соответственно определяют логическое И и логическое ИЛИ, символ «»– логическое отрицание, а символ «=>» является разделителем условной и заключительной частей правила (антецендента и консеквента). Общее описание правила вывода в индексном формате может быть представлено в следующем виде: [-]1j1…[-]iji…[-]njn[-]n+1jn+1…[-]k+ njk+1…[-]m+njm+n(w):<1,2>. Здесь порядок следования чисел соответствует очередности вводимых переменных, причем символ «,» разделяет правило на условную и заключительную части. До двоеточия записывается порядковый номер соответствующей ФП, после двоеточия – вид логической связки («1» – логическое И, «2» – логическое ИЛИ). Логическое отрицание задается символом «–». После определения правил вывода в одноименном редакторе можно утверждать, что СНВ полностью создана. Пример П10. Создание СНВ Рассмотрим следующую ситуацию. Необходимо оценить степень инвестиционной привлекательности конкретного бизнес-проекта на основании данных о ставке дисконтирования и периоде окупаемости. Шаг 1. Вызываем редактор для создания СНВ, набирая в командной строке fuzzy. Добавляем входную переменную посредством выбора в меню Edit пункта Addinput. В результате получаем следующую структуру СНВ: два входа, механизм нечеткого вывода по Мамдани, один выход. Объявляем первую переменную как discont, а вторую – period, которые соответственно будут представлять ставку дисконтирования и период окупаемости бизнес-проекта. Наименование выходной переменной, на основании которой принимается решение о степени инвестиционной привлекательности бизнес-проекта, задается как rate. Сохраним создаваемую модель под именем Invest. На рис. П9 представлено текущее состояние окна редактора СНВ. Шаг 2. Каждой входной и выходной переменной поставим в соответствие набор ФП. Данная процедура реализуется в редакторе ФП. Для discont определяем диапазон базовой переменной (Range) от 5 до 50 (единица измерения — проценты). Такой же диапазон выбираем для ее отображения (Display Range). Добавим три ФП, тип которых – trimf. Последовательно выделяя мышью отдельные ФП, присвоим наименования – small, middle, big соответственно небольшой, средней и большой ставке дисконтирования. Окно редактора ФП в текущем состоянии показано на рис. П10. Переменной period диапазон базовой переменной определен равным [3, 36] (единица измерения – месяцы), поставлены в соответствие три ФП типа gaussmfcнаименованиями – short, normal, long. Таким образом, переменная срока окупаемости бизнес-проекта будет принимать следующие значения: короткий, обычный и длительный срок окупаемости. 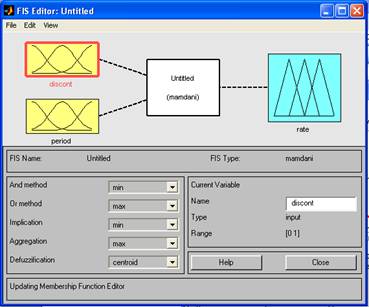 Рис. П9. Окно редактора системы нечеткого вывода. 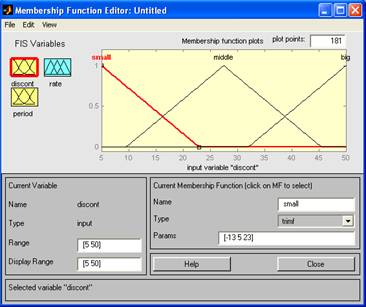 Рис. П10. Окно редактора ФП Наконец, для переменной rateопределяем: базовая переменная изменяет значение в диапазоне [0, 1], семантика описывается тремя ФП типа trimf' с наименованиями: bad, normal, good. Шаг 3. Заключительным этапом построения СНВ является определение набора правил, которые задают связь входных переменных с выходными. Для этого в редакторе правил вывода определим: ЕСЛИ discont = small И period = short TO rate = good ЕСЛИ discont = HE small И period = long TO rate = bad ЕСЛИ discont = middle И period = normal TO rate = normal ЕСЛИ discont = big И period = short TO rate = normal Текущее состояние окна редактора правил вывода показано на рис. П11. В расширенном формате отображения указанные правила вывода представляются следующим образом: 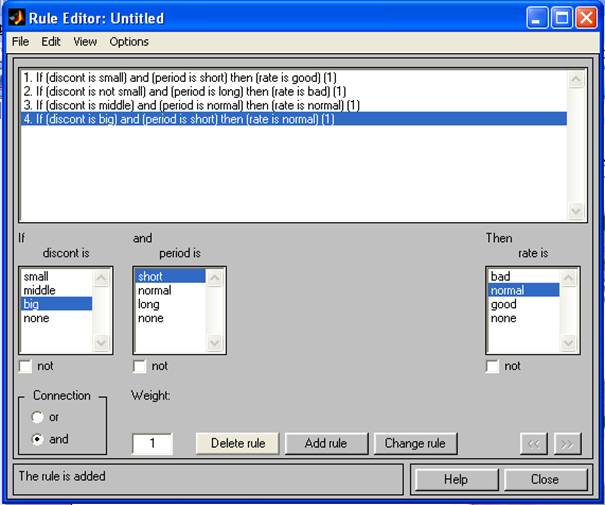 Рис. П11. Окно редактора правил вывода if(discont is small) and (period is short) then (rate is goad) (1) if(discont is not small) and (period is long) then (rate is bad) (1) if(discont is middle) and (period is normal) then (rate is normal) (1) if(discont is big) and (period is short) then (rate is normal) (1) При изменении формата на символьный правила вывода будут иметь вид: (discont == small) & (period == short) => (rate == good) (1) (discont = small) & (period == long) => (rate == bad) (1) (discont == middle) & (period== normal) => (rate== normal) (1) (discont == big) & (period == short) => (rate == normal) (1) Наконец, то же самое, но в индексном формате: 11,3(1) : 1 -13,1(1) : 1 22,2(1) : 1 31,2(1) : 1 Средство просмотра правил вывода Данное средство просмотра правил вывода позволяет отобразить процесс нечеткого вывода и получить результат. Главное окно средства просмотра состоит из нескольких графических окон, располагаемых по строкам и столбцам. Количество строк соответствует числу правил нечеткого вывода, а количество столбцов – числу входных и выходных переменных, заданных в разрабатываемой СНВ. Дополнительное графическое окно служит для отображения результата нечеткого вывода и операции дефазификации. В каждом окне отображается соответствующая ФП, уровень ее среза (для входных переменных) и вклад отдельной ФП в общий результат (для выходных переменных). В нижней части главного окна можно отобразить номера правил вывода в различных форматах вывода, отмечая их мышью. Для изменения формата в меню Optionsвыбирается пункт Ruledisplayformat. Изменение значений входных переменных допустимо двумя способами: 1) путем ввода в поле Input записи входного вектора, размерность которого равна количеству входных переменных; 2) щелчком мыши в любом графическом окне, которое относится к входной переменной. Входной вектор в каждом из этих вариантов определения исходных данных будет задавать набор красных вертикальных прямых. Для СНВ, рассмотренной в примере П10, при входном векторе [15 10] (ставка дисконтирования – 15 %, период окупаемости бизнес-проекта – 10 месяцев) результат (степень инвестиционной привлекательности) будет составлять 0,585 (рис. П12). 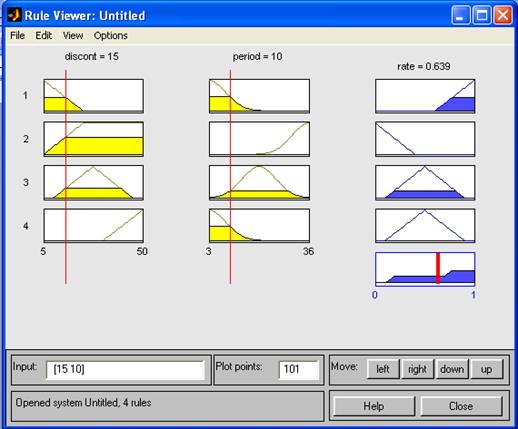 Рис. П12. Окно средства просмотра правил вывода (Ctrl+5) Средство просмотра поверхности вывода Средство просмотра поверхности вывода позволяет строить трехмерную поверхность как зависимость одной из выходных переменных от двух входных. Выбор входных и выходных переменных осуществляется посредством ниспадающих меню главного окна рассматриваемого программного средства. Количество выводимых линий по осям X и Yопределяется в полях ввода Xgrids, Ygrids. Поверхность вывода, соответствующая правилам вывода примера П10 показана на рис. П13. 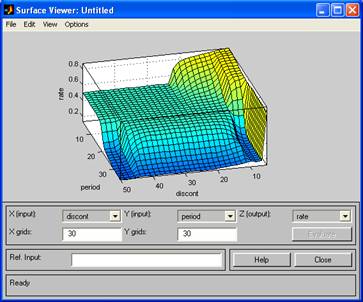 Рис. П13. Окно просмотра поверхности решений (Ctrl+6) Построение нечетких систем типа Суджено Рассмотрим построение СНВ двумя редакторами – СНВ и ФП. Для построения СНВ типа Суджено необходимо в меню File выбрать пункт NewFIS -> Sugeno. Количество входных и выходных переменных определяется так же, как и при построении СНВ типа Мамдани. Редактор ФП. Для СНВ типа Суджено изменения касаются только схемы определения ФП для выходных переменных. ИНЛ в среде Matlabпозволяет разрабатывать два вида нечетких моделей. Первая модель – это нечеткая модель Суджено нулевого порядка. Нечеткое правило вывода имеет следующий вид: if x is A and у is В then z= к, где А и В – нечеткие множества антецедента; к –четко заданная константа консеквента. Для построения такой модели при добавлении ФП необходимо выбрать тип – константа (constant) и задать в качестве параметра ФП численное значение соответствующей константы. Вторая модель – нечеткая модель Суджено первого порядка. Для нее нечеткое правило вывода записывается следующим образом: if x as A and у is В then z = p·x+q·y+r, где р, q и r – константы. В данном случае тип ФП – линейная зависимость (linear). Для определения параметров ФП необходимо ввести вектор, элементы которого соответствуют численным значениям констант консеквента. Работа с редактором правил вывода, а также со средствами просмотра правил и поверхности вывода выполняется аналогично случаю построения СНВ по Мамдани. Пример нечеткого вывода по Суджено с использованием нечеткой модели нулевого порядка и правил вывода, определенных выше, представлен на рис. П14 (выходная переменная имеет три значения: bad, normal, good, которые задаются соответственно тремя константами – 0, 0.5, 1). 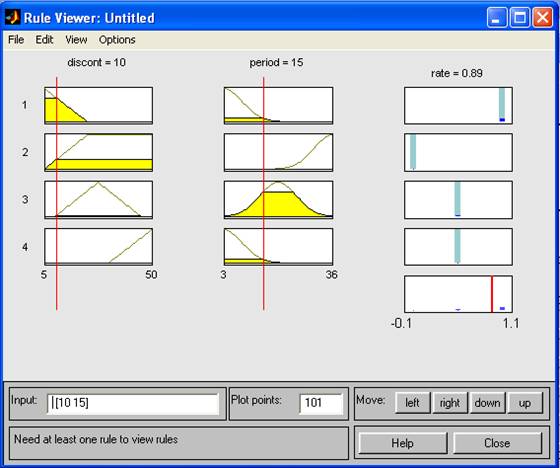 Рис. П14. Окно просмотра правил вывода (вывод по Суджено) |