Министерство науки и высшего образования РФ федеральное государственное бюджетное

образовательное учреждение высшего образования

«Самарский государственный технический университет» (ФГБОУ ВО «СамГТУ»)

Кафедра «Вычислительная техника»

ГРАФИЧЕСКИЕ

СИСТЕМЫ КОМПЬЮТЕРОВ

КУРСОВАЯ РАБОТА

на тему ВЕКТОРНЫЙ ГРАФИЧЕСКИЙ РЕДАКТОР

Вариант индивидуального задания №93
Руководитель

Доцент кафедры «Вычислительная техника» Пугачев А.И.

Выполнил обучающийся группы 3-ИАИТ-3 Ушков Д.Е.

Самара

2022

Оглавление

---

1. Техническое задание для курсовой работы

Описание метода в оглавлении. Разработать программу объектно-ориентированного графического редактора, обеспечивающего выполнение следующих основных функций:

• 
  выбор, размещение на экране и визуализация примитивов из заданного набора;
  
• 
  синтез более сложных фигур с помощью теоретико-множественных операций (ТМО) как над примитивами, так и над ранее синтезированными фигурами;
  
• 
  выделение любого объекта, выведенного на экран, и выполнение над ним любой последовательности геометрических преобразований из заданного набора в интерактивном режиме;
  
• 
  выделение любого объекта на экране и его удаление.
  

Рисунок 1. Техническое задание из методички

Вариант 93

Нужно сделать:

1. 
   ER - Кубический сплайн
   
2. 
   Pgn - Правильный n-угольник
   
3. 
   Str1 - Стрелка 1
   
4. 
   Rc - Поворот вокруг заданного центра на произвольный угол
   
5. 
   Sxyf - Пропорциональное масштабирование относительно центра фигуры
   
6. 
   MV - Зеркальное отражение относительно вертикальной прямой
   
7. 
   / - разность
   
8. 
    - объединение
   

2. Реализация

2.1 Вспомогательный класс MyPoint:

Содержит в себя поля для решение таких задач как:

Определение функции и фигуры

Определение было или не было сделано ТМО (Теоретико-Множественных Операции)

Содержит в себе переменную Thirst для вычисления матриц 3х3

public class MyPoint

{

public float X;

public float Y;

public float Third;

public bool Function;

public bool DoTmo;
public MyPoint (float x = 0.0f, float y = 0.0f, float third = 1.0f)

{

X = x;

Y = y;

Third = third;

Function = false;

DoTmo = false;

}
public Point ToPoint () => new Point((int) X, (int) Y);

}

А также благоприятствует более точным вычислениям благодаря использованию другого типа данных. Float, а не int.

2.2 Вспомогательная структура M

private struct M

{

public float X { get; }

public int Dq { get; }
public M (float x, int dQ)

{

X = x;

Dq = dQ;

}

}

Данная структура нужна для реализации операции ТМО (теоретико-множественные-операции). В нем представлена координата x типа float и вес Dq типа int.

2.3 Вспомогательные методы

Здесь мы рассмотрим основные методы используемые для реализации программы.

---

2.3.1 Fill - закрашивание многоугольника

Метод Fill – закрашивание многоугольника внутри. Сначала идет проверка на рисование границ многоугольника (вызывается метод PaintingLineInFigure, потом вызывается метод, который ищет минимальный и максимальный Y у данной фигуры (вызывается метод SearchYMinAndMax). Дальше идет цикл, который проходит по всем Y, начиная с минимального и заканчивая максимальным. В этом цикле программа имеется еще один цикл, который проходит по всем точкам нашей фигуры. В шаге второго цикла всегда рассматриваются точки с позицией i и i+1. Эти точки передаются в метод (CheckIntersection), который добавляет координату X в массив координат иксов на прямой Y. После окончания внутреннего цикла мы рассматриваем последнюю пару точек: последняя и первая. После чего сортируем наш массив и выводим отрезки списка x (под отрезками я понимаю i и i+1 координату). Для следующей прямой Y мы очищаем наш список X.

private void Fill (List pointFs)

{

if (pointFs[0].Function)

{

PaintingLineInFigure(pointFs);

return;

}
var arr = SearchYMinAndMax(pointFs);

var min = arr[0];

var max = arr[1];

var xs = new List();
for (var y = (int) min; y < max; y++)

{

var k = 0;

for (var i = 0; i < pointFs.Count - 1; i++)

{

k = i < pointFs.Count ? i + 1 : 1;

xs = CheckIntersection(xs, i, k, y, pointFs);

}
xs = CheckIntersection(xs, k, 0, y, pointFs);

xs.Sort();
for (var i = 0; i + 1 < xs.Count; i += 2)

_graphics.DrawLine(_drawPen, new Point((int) xs[i], y), new Point((int) xs[i + 1], y));
xs.Clear();

}
pictureBox1.Image = _bitmap;

}

Рассмотрим вспомогательные методы, которые были использованы в методе выше.

2.3.2 PaintingLineInFigure – рисование ребер многоугольника

Границы многоугольника рисуются, если пользователь выбрал отрисовку с границами. Внутри метода, имеется условие на проверку выбора пользователя и проверку количества точек. Если проверка прошла успешно, то программа проходит по всем точкам и рисует границы (также дополнительно рассматриваем последнюю пару точек: последняя и первая).

private void PaintingLineInFigure (List points)

{

for (var i = 0; i < points.Count - 1; i++)

_graphics.DrawLine(_drawPen, points[i].ToPoint(), points[i + 1].ToPoint());

pictureBox1.Image = _bitmap;

}

2.3.3 SearchYMinAndMax – нахождение минимального и максимального Y

Работа метода начинается с проверки количества точек. Если их нет, то метод сразу возвращает нули. Дальше программа заполняет первыми значениями списка точек переменные min и max. После идет цикл, в котором происходит сравнение конкретной точки с переменными min и max, и в зависимости от сравнения идет действие: либо присвоение переменным значение точки по координате Y, либо проход к следующей точке.

private float[] SearchYMinAndMax (List pointFs)

{

if (pointFs.Count == 0)

return new float[] { 0, 0 };
var min = pointFs[0].Y;

var max = pointFs[0].Y;

foreach (var t in pointFs)

{

min = t.Y < min ? t.Y : min;

max = t.Y < max ? max : t.Y;

}
min = min < 0 ? 0 : min;

max = max > pictureBox1.Height ? pictureBox1.Height : max;

return new[] { min, max };

}

2.3.4 CheckIntersection – добавление точки при пересечении с прямой Y

Добавление точки происходит, если выполняется условие пересечение в методе Check. Сначала идет нахождение пересечения, то есть координату X (находиться путем нахождения уравнения двух прямых)

private static List CheckIntersection (List xs, int i, int k, int y, List pointFs)

{

if (Check(i, k, y, pointFs))

{

var x = -((y * (pointFs[i].X - pointFs[k].X)) - pointFs[i].X * pointFs[k].Y +

pointFs[k].X * pointFs[i].Y)

/ (pointFs[k].Y - pointFs[i].Y);

xs.Add(x);

}
return xs;

}

2.3.5 Check – проверка пересечение прямой Y с отрезком

Check – метод, который проверят пересечения прямой Y с отрезком, состоящим из точек I и k.

private static bool Check (int i, int k, int y, List pointFs) =>

(pointFs[i].Y < y && pointFs[k].Y >= y) || (pointFs[i].Y >= y && pointFs[k].Y < y);

3. Реализация функции Кубического сплайна

Для реализации функции Кубического сплайна нам потребуется добавление точки и построение самой функции по сохраненным ранее точкам.

В свойствах pictureBox настраиваем обработчик отклика мышки, то есть при нажатии на панель у нас будет вызываться метод PictureMouseDown (рисунок 2).



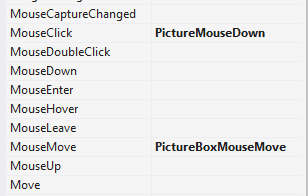
Рисунок 2. Свойство формы

Данный метод отлавливает местоположение курсора и другие дополнительные данные, и в зависимости от выбранной операции с многоугольником выполняет действия. Код данного метода представлен ниже:

private void PictureMouseDown(object sender, MouseEventArgs e)

{

_operation = comboBoxGeometric.SelectedIndex;

pictureBoxMousePosition = e.Location;

if (_operation == 0 && _isPaintFigure)

{

switch (_figure)

{

case 's':

if (_points.Count < 3)

{

AddPoint(e);

return;

}
AddPoint(e);

CreateCubeSpline();

break;

case 'p':

{

if (_points.Count < 2)

{

AddPoint(e);

return;

}
CreateParallelogram();

_points.Clear();

break;

}

default:

CreateFlag(e);

break;

}
Fill(_figures[_figures.Count - 1]);

_isPaintFigure = false;

}

else if (_operation == 4 && _figures.Count != 0)

{

ThisFigure(e);

}

// Добавление точки

else if (MouseButtons.Left == e.Button)

{

AddPoint(e);

if (_operation == 3)

{

AddPoint(new MyPoint(pictureBox1.Width, _points[_points.Count - 1].Y));

_graphics.DrawLine(_drawPen,

new Point(0, (int) _points[0].Y),

_points[_points.Count - 1].ToPoint());

pictureBox1.Image = _bitmap;

}

}

// Рисование и добавление фигуры в общей список фигур

else

{

Fill(_points);

_figures.Add(_points.ToList());

_points.Clear();

}
pictureBox1.Image = _bitmap;

}

Рассмотрим подробней действия с зарисовкой. Первое условие проверяет, рисуется ли сейчас специальная фигура (под специальной фигурой, я понимаю фигуру, точки которой задаются сразу, в будущем это будет многоугольник или стрелка 1). Следующее условие проверяет рисуется ли сейчас Кубический сплайн. Дальше идет условие на проверку нажатия правой кнопкой мыши, данное условие применяется, когда пользователь рисует многоугольник сам и в итоге хочет его закрасить, чтобы ему его закрасить, нужно нажать на правую кнопку мыши, что и отлавливает данное условие. Если ни одно условие не выполнилось, то программа переходит в метод добавления точки.

Для рисования Кубического сплайна пользователю нужно выбрать в combobox фигур «Кубический сплайн», рисунок 3.



Рисунок 3. Отображение компонента «Кубический сплайн»

В данном методе идет вычисление координат для Кубического сплайна. Результат работы построения Кубического сплайна представлен на рисунке 4.

// Кубический сплайн

private void CreateCubeSpline()

{

var function = new List();

var l = new PointF[4];

var pv1 = _points[0].ToPoint();

var pv2 = _points[0].ToPoint();
const double dt = 0.04;

double t = 0;

double xt, yt;

Point ppred = _points[0].ToPoint(), pt = _points[0].ToPoint();
pv1.X = (int) (4 * (_points[1].X - _points[0].X));

pv1.Y = (int) (4 * (_points[1].Y - _points[0].Y));

pv2.X = (int) (4 * (_points[3].X - _points[2].X));

pv2.Y = (int) (4 * (_points[3].Y - _points[2].Y));
l[0].X = 2 * _points[0].X - 2 * _points[2].X + pv1.X + pv2.X; // Ax

l[0].Y = 2 * _points[0].Y - 2 * _points[2].Y + pv1.Y + pv2.Y; // Ay

l[1].X = -3 * _points[0].X + 3 * _points[2].X - 2 * pv1.X - pv2.X; // Bx

l[1].Y = -3 * _points[0].Y + 3 * _points[2].Y - 2 * pv1.Y - pv2.Y; // By

l[2].X = pv1.X; // Cx

l[2].Y = pv1.Y; // Cy

l[3].X = _points[0].X; // Dx

l[3].Y = _points[0].Y;

function.Add(new MyPoint(ppred.X, ppred.Y) {Function = true});

while (t < 1 + dt / 2)

{

xt = ((l[0].X * t + l[1].X) * t + l[2].X) * t + l[3].X;

yt = ((l[0].Y * t + l[1].Y) * t + l[2].Y) * t + l[3].Y;
pt.X = (int) Math.Round(xt);

pt.Y = (int) Math.Round(yt);
_graphics.DrawLine(_drawPen, ppred, pt);

ppred = pt;

function.Add(new MyPoint(ppred.X, ppred.Y));

t += dt;

}
_figures.Add(function);

}


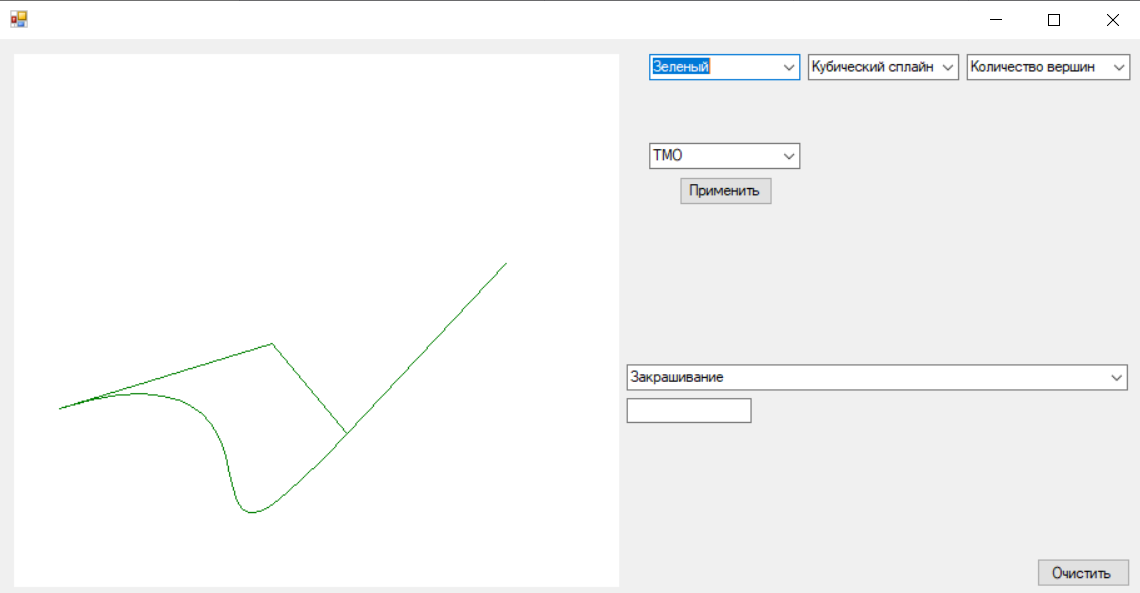
Рисунок 4. Реализация Кубического сплайна

4. Реализация создания фигур

Для создания готовой фигуры я использовал следующие comboBox: Цвет, Фигуры, Количество вершин (для правильного n-угольника). Для изменения цвета фигуры можно изменить comboBox Цвета (по умолчанию черный).

private void ComboBoxFigures (object sender, EventArgs e)

{

switch (comboBoxFigures.SelectedIndex)

{

case 0:

_figure = 's';

break;

case 1:

_figure = 'p';

break;

default:

_figure = 'c';

break;

}
_isPaintFigure = true;

}

Для рисования выбранной фигуры, пользователь должен выбрать в «Геометрическое преобразование» - Закрашивание, после чего нажать любой кнопкой мыши на pictureBox, тем самым вызвав выполнения условия в обработчике события PictureMouseDown.

private void PictureMouseDown (object sender, MouseEventArgs e)

{

_operation = comboBoxGeometric.SelectedIndex;

pictureBoxMousePosition = e.Location;

if (_operation == 0 && _isPaintFigure)

{

switch (_figure)

{

case 's':

if (_points.Count < 3)

{

AddPoint(e);

return;

}
AddPoint(e);

CreateCubeSpline();

break;

case 'p':

CreateRegularPolygon(e);

_points.Clear();

break;

default:

CreateStrelka1(e);

break;

}
Fill(_figures[_figures.Count - 1]);

_isPaintFigure = false;

}

else if (_operation == 4 && _figures.Count != 0)

{

ThisFigure(e);

4.1 Fill – закрашивание фигуры.

Рассмотрим подробней метод Fill. Данный метод закрашивает фигуру. После закрашивания, идет добавление фигуры в список фигур, путем клонирования. В самом конце очищается список точек для создания фигуры и отрисовка в pictureBox из буфера bitmap.

private void Fill (List pointFs)

{

if (pointFs[0].Function)

{

PaintingLineInFigure(pointFs);

return;

}
var arr = SearchYMinAndMax(pointFs);

var min = arr[0];

var max = arr[1];

var xs = new List();
for (var y = (int) min; y < max; y++)

{

var k = 0;

for (var i = 0; i < pointFs.Count - 1; i++)

{

k = i < pointFs.Count ? i + 1 : 1;

xs = CheckIntersection(xs, i, k, y, pointFs);

}
xs = CheckIntersection(xs, k, 0, y, pointFs);

xs.Sort();
for (var i = 0; i + 1 < xs.Count; i += 2)

_graphics.DrawLine(_drawPen, new Point((int) xs[i], y), new Point((int) xs[i + 1], y));
xs.Clear();

}

4.2 ToAndFromCenter - перемещение фигуры в центр и обратно.

В зависимости от параметра start, будет сформирована специальная матрица преобразований.

private static void ToAndFromCenter (bool start, MyPoint e, List pointFs)

{

if (start)

{

float[,] toCenter =

{

{1, 0, 0},

{0, 1, 0},

{-e.X, -e.Y, 1}

};

Calculation(toCenter, pointFs);

}

else

{

float[,] fromCenter =

{

{1, 0, 0},

{0, 1, 0},

{e.X, e.Y, 1}

};

Calculation(fromCenter, pointFs);

}

}

4.3 Создание фигуры «Правильный n-угольник»

Для создания фигурыправильный n-угольник, нужно повторить все вышеописанные действия с единственным уточнением: выбор конкретной фигуры, в данном случае правильный многоугольник (ComboBoxFigures), а так же выбор количества вершин (ComboBoxVertex). Тогда программа при заходе в метод CreateRegularPolygon добавит фигуру правильного n-угольника.

Результат работы программы представлен на рисунке 5.

private void CreateRegularPolygon (MouseEventArgs e)

{

var count = comboBoxVertex.SelectedIndex + 3;

var points = new List();

const int length = 50;

var r = length / (2 * Math.Sin(Math.PI / count));

for (var angle = 0.0; angle <= 2 * Math.PI; angle += 2 * Math.PI / count)

{

var x = (int) (r * Math.Cos(angle));

var y = (int) (r * Math.Sin(angle));

points.Add(new MyPoint((float) (r + x), (float) (r + y)));

}
_figures.Add(points);

ToAndFromCenter(false, new MyPoint(e.X - length, e.Y - length), _figures[_figures.Count - 1]);

}



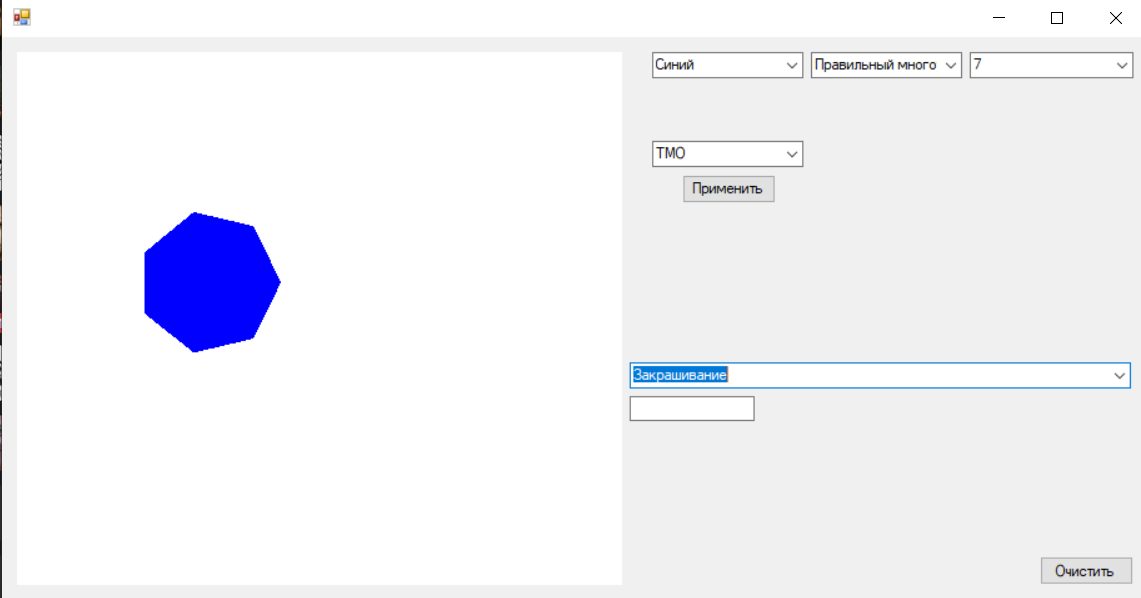
Рисунок 5. Закрашенная фигура «Правильный n-угольник»

4.4 Создание фигуры «Стрелка 1»

Для создания фигуры Стрелка 1, нужно повторить все вышеописанные действия с единственным уточнением: выбор конкретной фигуры, в данном случае Стрелка 1. Тогда программа перейдет в метод CreateStrelka1 и добавит фигуру Стрелка 1.

Результат работы программы представлен на рисунке 6.

private void CreateStrelka1 (MouseEventArgs e)

{

var points = new List

{

new MyPoint(e.X - 100, e.Y - 20),

new MyPoint(e.X + 10, e.Y - 20),

new MyPoint(e.X + 10, e.Y - 50),

new MyPoint(e.X + 100, e.Y),

new MyPoint(e.X + 10, e.Y + 50),

new MyPoint(e.X + 10, e.Y + 20),

new MyPoint(e.X - 100, e.Y + 20)

};

_figures.Add(points);

}



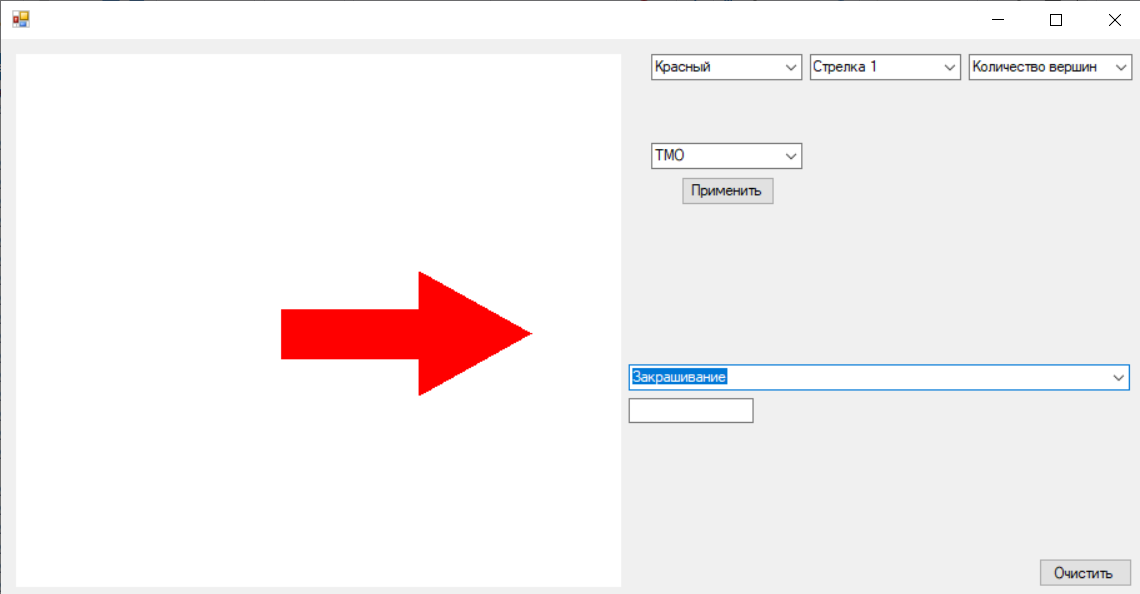
Рисунок 6. Закрашенная фигура «Стрелка 1»

4. Поворот вокруг заданного центра на произвольный угол

Для реализации данного действия, нам нужно иметь готовую фигуру, то есть в форме мы должны увидеть закрашенную фигуру, например, как на рисунке 2. Дальше пользователь должен изменить действие в СomboBox «Геометрическое преобразование» с Закрашивания на Поворот вокруг заданного центра. За счет прописанного внутри конструктора эвента на отслеживание действий мышки

MouseWheel += TransformationGeometric;

5.1 GeometricTransformation- определяет над каким количеством фигур нужно сделать преобразование

Данный метод нужен для того, чтобы узнать, над одной фигурой ведется преобразование или несколькими. Если несколькими, то нужно вызывать одну и туже операцию для нескольких фигур и производить над ними ТМО.

private void TransformationGeometric (object sender, MouseEventArgs e)

{

if (_figures.Count == 0) return;

var figureBuff = _figures[_figures.Count - 1];

if (figureBuff[0].DoTmo)

{

OperationGeometric(e, figureBuff);

OperationGeometric(e, _figures[_figures.Count - 2]);

_graphics.Clear(Color.White);

Tmo();

pictureBox1.Image = _bitmap;

}

else

OperationGeometric(e, figureBuff);

}

5.2 OperationGeometric – определяет действие с фигурой

Данный метод нужен для геометрических преобразований. В зависимости от operation будет выполнена следующее преобразование. Для вращений объекта нужно чтобы operation == 1. Дальше переходим в метод Rotation.

private void OperationGeometric (MouseEventArgs e, List buff)

{

_operation = comboBoxGeometric.SelectedIndex;

if (_figures.Count == 0) return;

switch (_operation)

{

case 1:

Rotation(e.Delta, e, buff);

break;

case 2:

Zoom(e.Delta, e, buff);

break;

case 3:

Mirror(buff, e);

break;

}
_graphics.Clear(pictureBox1.BackColor);

Fill(buff);

}

5.3 Rotation – метод для вычисления координат при вращении фигуры

Рассмотрим метод Rotation. Переменная updateAlpha хранит в себе значение угла, на который был повернута фигура. Mouse – вращение колесика, либо в положительную, либо в отрицательную сторону. textBox1.text нужен для отслеживания пользователем угла вращения. Дальше идет определение заданного центра относительно которого мы будем вращать фигуру с помощью объекта MouseEventArgs, который отслеживает положение курсора, который задается центр. Это нужно чтобы фигура повернулась относительно заданного центра.

private void Rotation (int mouse, MouseEventArgs em, List pointFs)

{

float alpha = 0;

if (mouse > 0)

{

alpha += 0.0175f;

_updateAlpha++;

}

else

{

alpha -= 0.0175f;

_updateAlpha--;

}
textBox1.Text = _updateAlpha.ToString();

var e = new MyPoint(em.X, em.Y);

ToAndFromCenter(true, e, pointFs);
float[,] matrixRotation =

{

{(float) Math.Cos(alpha), (float) Math.Sin(alpha), 0.0f},

{-(float) Math.Sin(alpha), (float) Math.Cos(alpha), 0.0f},

{0.0f, 0.0f, 1.0f}

};
for (var i = 0; i < pointFs.Count; i++)

pointFs[i] = Matrix_1x3_x_3x3(pointFs[i], matrixRotation);
ToAndFromCenter(false, e, pointFs);

}

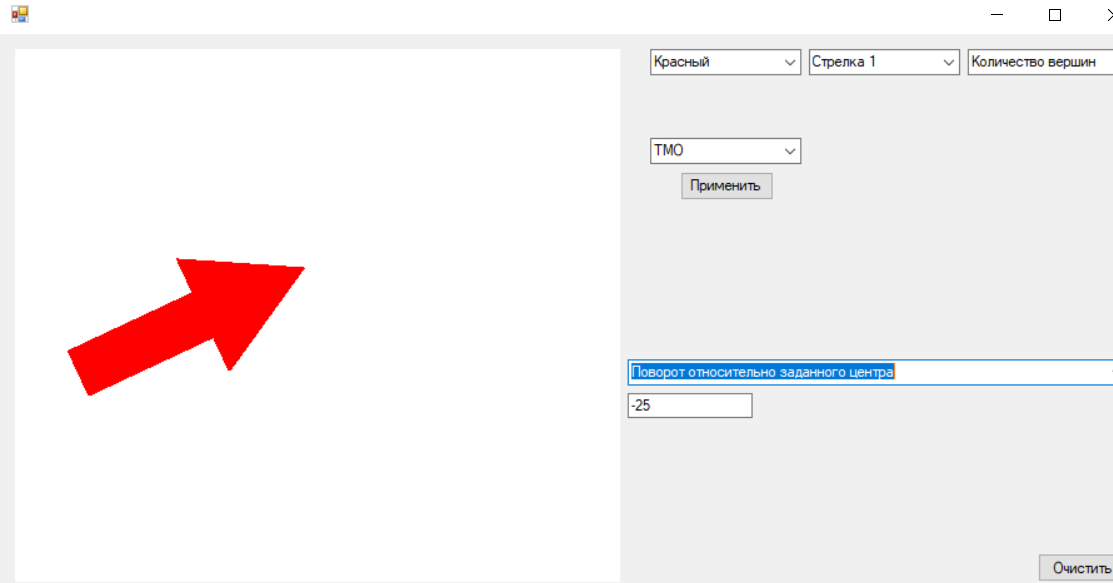
Рисунок 7. Поворот фигуры «Стрелка 1»

4. Пропорциональное масштабирование относительно центра фигуры

Для реализации данного действия нам нужно иметь фигуру как на рисунке 5 или 6. Дальше в СomboBox «Геометрическое преобразование» выбираем действие пропорциональное масштабирование относительно центра фигуры.

После прокрутки колесика, программа заходит в метод OperationGeometric (случай, как с вращением фигуры). В данном методе выполняется условие if (operation== 2) и программа переходит в метод Zoom.

6.1 Zoom – метод масштабирования фигуры

Данный метод нужен для масштабирования фигуры в зависимости от выбора operation. Рассмотрим переменные данного метода:

Переменные Sx & Sy есть коэффициенты масштабирования

Matrix – матрица для увеличения/уменьшения фигуры.

E – принимает координату центра фигуры, относительно которой будет масштабироваться фигура.

private void Zoom (float zoom, MouseEventArgs em, List points)

{

if (zoom <= 0) zoom = -0.1f;

else zoom = 0.1f;
var sx = 1 + zoom;

var sy = 1 + zoom;

float[,] matrix =

{

{sx, 0, 0},

{0, sy, 0},

{0, 0, 1}

};
var arY = SearchYMinAndMax(points);

var arX = SearchXMinAndMax(points);
var e = new MyPoint((arY[0] + arY[1]) / 2, (arX[0] + arX[1]) / 2);

ToAndFromCenter(true, e, points);
for (var i = 0; i < points.Count; i++)

points[i] = Matrix_1x3_x_3x3(points[i], matrix);
ToAndFromCenter(false, e, points);

}

Рисунок 8. Пропорциональное масштабирование относительно центра фигуры

4. 
   Зеркальное отражение относительно вертикальной прямой
   

Для реализации данного действия нам нужно иметь фигуру как на рисунке 5. Дальше пользователь должен изменить действие в comboBox «Геометрическое преобразование» с Закрашивания на Зеркальное отражение относительно вертикальной прямой. И задаем вертикальную прямую, двумя точками, нажав левой кнопкой мыши в pictureBox, относительно которой мы хотим сделать отражение.

После прокрутки колесика, программа заходит в метод OperationGeometric. (случай, как с вращением фигуры) и если выполняется условие if (operation == 3) и программа переходит в метод Mirror.

7.1 Mirror – метод отражения фигуры

В нашем случае, данный метод нужен для отражения фигуры относительно вертикальной прямой. Рассмотрим данный метод:
private void Mirror (List points, MouseEventArgs e)

{

var arrY = SearchYMinAndMax(points);

var pointCenterMirror = new MyPoint(e.X, (arrY[1] + arrY[0]) / 2);

ToAndFromCenter(true, pointCenterMirror, points);
var s = new float[,]

{

{-1, 0, 0},

{0, 1, 0},

{0, 0, 1}

};

Calculation(s, points);
ToAndFromCenter(false, pointCenterMirror, points);

_points.Clear();

_graphics.DrawLine(_drawPen, new Point(e.X, 0), new Point(e.X, pictureBox1.Height));

}
Реализация данного действия происходит с использованием матрицы.



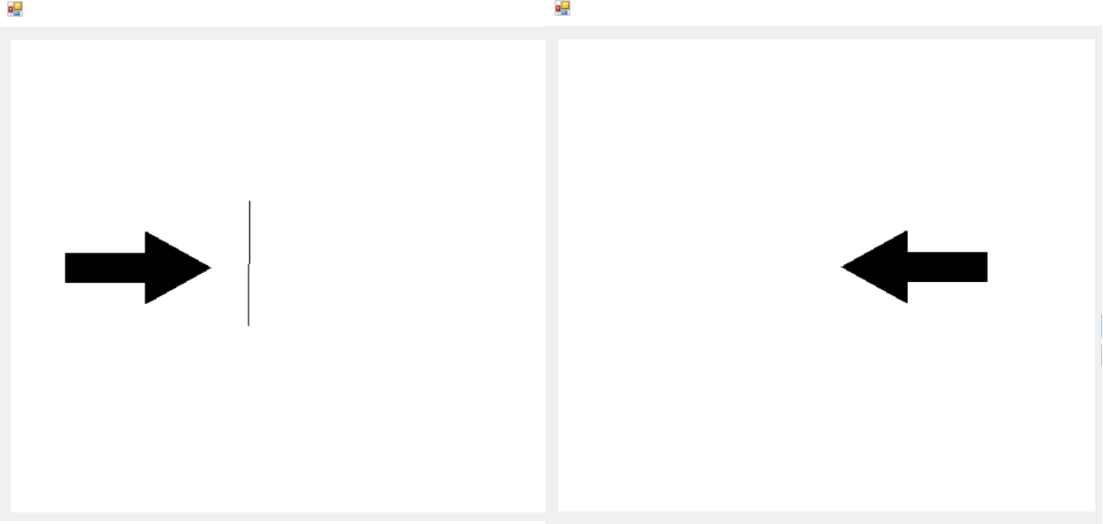
Рисунок 9. Зеркальное отражение относительно вертикальной прямой

4. Реализация теоретико-множественных операций

Для реалиазации данной операции пользовтель должен нарисовать 2 фигуры, выбрать операцию в comboBox «ТМО» и нажать на кнопку «Применить».

Рассмотрим более подробно шаг с нажатием на кнопки ТМО.

При нажатии на кнопку программа переходит в метод ButtonTmo. В данном методе сначала выполняется операция ТМО, а потом достается информация из буффера в pictureBox.

private void ButtonTmo(object sender, EventArgs e)

{

_graphics.Clear(Color.White);

Tmo();

pictureBox1.Image = _bitmap;

}

Рассмотрим подробно метод Tmo.

8.1 Tmo – алгоритм построения фигур с помощью ТМО

Реализация начинается с получения двух последних фигур. После у этих двух фигур находится их минимальный и максимальный Y (для минимума выбирается минимальный, для максимума выбирается максимальный).

Дальше идет цикл от минимального до максимального Y сначала идет получение координат пересечения фигур A и В с прямой Y. Эти координаты находятся с помощью метода CalculationListXrAndXl(Y). После идет заполнение массива объектами M. Вес фигуры А = 2, В = 1. После массив нужно отсортировать по возрастанию M[i].х.

Потом создается еще один цикл, который проходит по массиву элементов M. В качестве текущего значения переменной x всегда выбирается очередное значение M[i].x. При этом функция Q изменяется на величину M[i].dQ.

Особым случаем является такой, когда первым элементом массива M оказывается правая граница сег-мента, т.е. M[1].x >= Xemin и M[1].dQ < 0. В этой ситуации список Xrl левых границ сегментов необходимо дополнить значением Xemin.

Если в очередном цикле предыдущее значение Q не входило в SetQ, а новое ее значение Qnew в SetQ входит, значит x – координата левой границы сегмента результирующей области. Это значение записывается в Xrl. Аналогичным образом устанавливаются случаи, в которых x является координатой правой границы. Такие значения x записывается в массив Xrr.

По завершению цикла обработки M число левых границ в массиве Xrl должно быть равно числу правых границ в массиве Xrr. Если же в этот момент Q не принаджежит SetQ, значит не найдена правая граница по-следнего сегмента. Тогда за нее принимается правая граница Xemax области вывода.

В примере используется две фигуры:

А – Правильный многоугольник,

B – Стрелка 1.



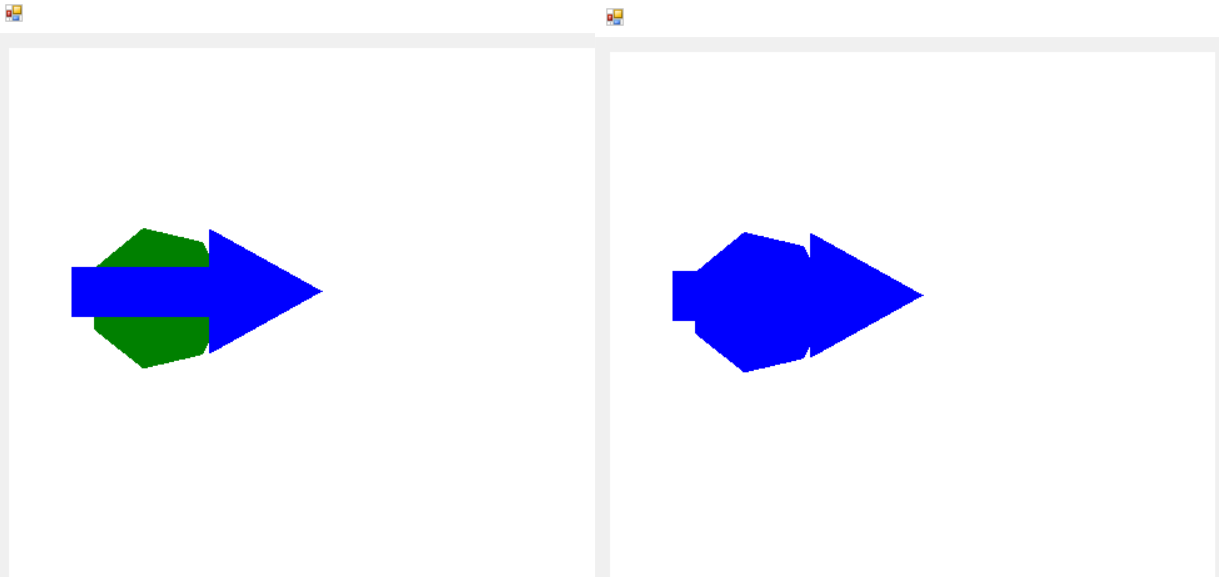
Рисунок 10. Реализация объединения фигур.



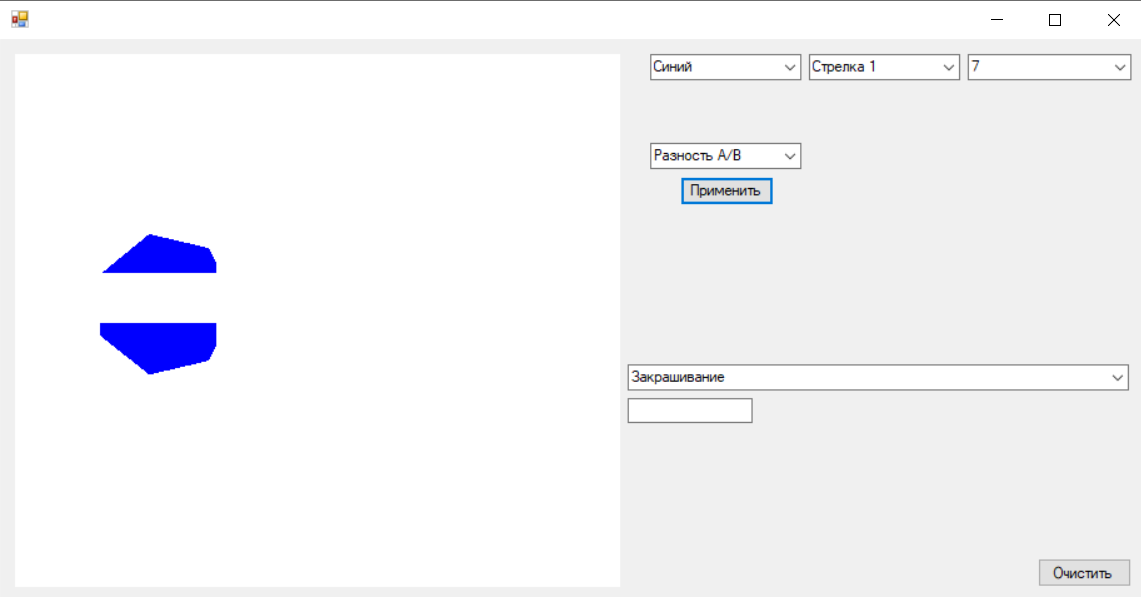
Рисунок 11. Реализация разности фигур A/B



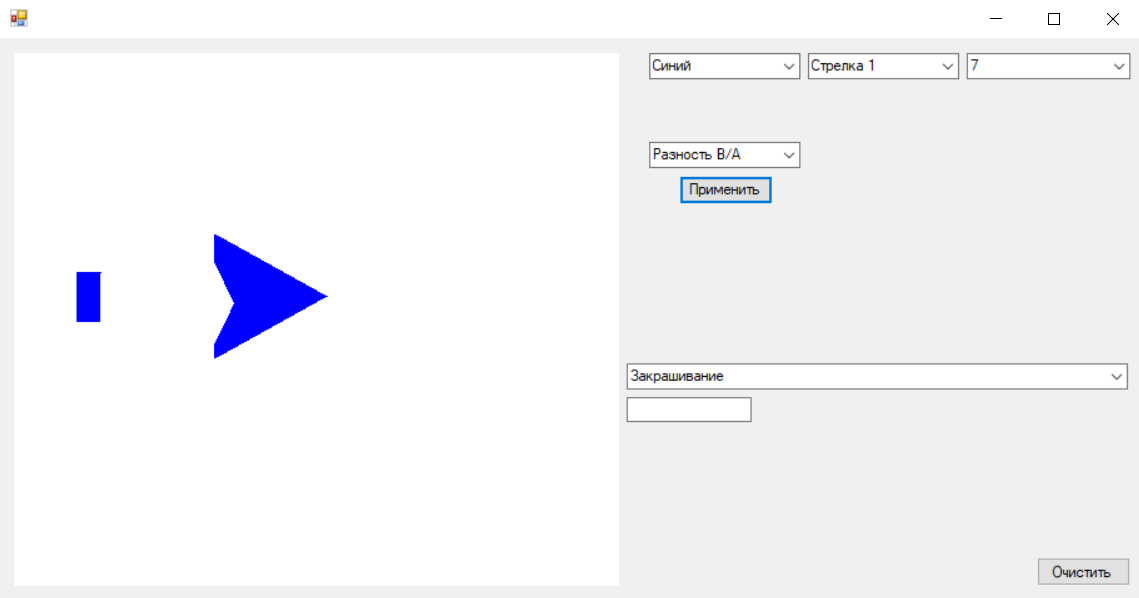
Рисунок 12. Реализация разности фигур B/A

4. Руководство использования

Для построение Кубического сплайна нужно в comboBox фигур выбрать «Кубический сплайн», после чего начать нажимать левой кнопкой мышки на экран. После выбора четырех точек в pictureBox левой кнопкой мыши кубический сплайн будет построен.

Для очищения формы, нужно нажать на кнопку «Очистить».

Построение многоугольника можно выполнить несколькими вариантами:

1. 
   Нажатием левой кнопки мыши строить вершины многоугольника и при окончании построения нажать правую кнопку мыши
   
2. 
   Выбрать в операциях с геометрическими преобразование - закрашивание, после выбрать нужную фигуру и нажать на форму любой кнопкой мышки.
   

Для того чтобы повернуть фигуру на определенный угол, нужно нарисовать фигуру как сказано выше, и потом выбрать в операциях с многоугольником вращение.

Для зеркального отражения и масштабирования нужно сделать тоже самое.

---

Смотрите также файлы

• A печеночной вене b лимфатических сосудах c.pdf

• Паспорт серия N, выдан " " г.docx

• Урок 15 Тема урока Научный комплексвершина экономики.docx

• Задача 3 по дисциплине мдк 01. 02 Управление технической эксплуатацией холодильного оборудования (по отраслям) и контроль за ними.docx

• Из них 20 тысяч км.docx