ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Извлечение корня n-й степени из единицы.
1 = cos0+i sin0
= cos
+i sin , 
.Корни расположены на окружности единичного радиуса и делят эту окружность на n равных частей.
, где 
принимает ровно 
значений. Теорема 1.
Все значения корня n–той степени из комплексного числа z можно получить умножением одного из них на все корни из 1.
Доказательство:
Возьмём =
= 
(cos
+i sin ), где s–фиксированное число.1, 2,…, n – так обозначим все корни
.Домножим каждый из корней 1,…, n на . Они разные, все являются корнями n–той степени из z, ибо (i)n = z и их
штук.Теорема доказана.
Теорема 2.
Произведение двух корней n–той степени из единицы есть корень степени n из единицы.
Следствие.
Степень корня n–той степени из единицы есть корень степени n из единицы.
Все ли корни из 1 равноправны?
n=4 ; 1, –1, i, –i — корни из единицы.
i; –i — первообразные корни; если i возводить в степени 0, 1, 2, 3, то получим все корни.
Определение 1.
Корень n–той степени из 1 называется первообразным, если он не даёт единицу в степени меньше, чем n.
-
Показательная форма комплексного числа. Действия над комплексными числами в показательной форме.
Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой
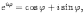(17.10)которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов. Эта теория будет изложена в курсе математического анализа.
Пусть комплексное число
в тригонометрической форме имеет вид 
. На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим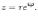 
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь
, 
. 
-
13. Операции над многочленами и их свойства.