ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРТСВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА IКАФЕДРА: «Электротехника и теплоэнергетика»Лабораторная работа №26Выполнил Студент гр. АС-907 Коршунов А. Санкт-Петербург2020Содержание

1. 
   Перечень условных обозначений
   
2. 
   Введение
   
3. 
   Схема электрической цепи
   
4. 
   Векторная диаграмма
   
5. 
   Согласное включение
   
6. 
   Встречное включение
   
7. 
   Диаграмма при трансформаторном включении
   
8. 
   Заключение
   

Перечень условных обозначений - катушки индуктивности - резистор L – индуктивность катушки, ГнR – электрическое сопротивление, ОмM – взаимная индукция, ГнU – напряжение, ВХ – реактивное сопротивление, ОмI – сила тока, АВведениеЦелью работы является определение параметров линейных индуктивно-связанных катушек, исследование последовательного, параллельного соединения и трансформаторного включения.Программа работы:

1. 
   Для схемы, изображенной на рис. 1 обьяснить построение векторных диаграмм при согласном рисунке (рис. 2а) и встроенном (рис. 2б) включениях последовательно соединительных индуктивно связанных катушек.
   
2. 
   Обьяснить построение векторной диаграмы (рис. 3) при трансформаторном включении катушек.
   

---

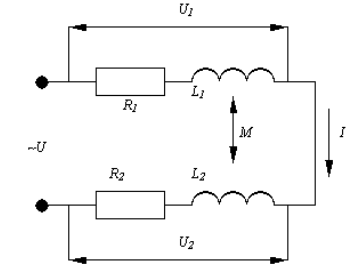
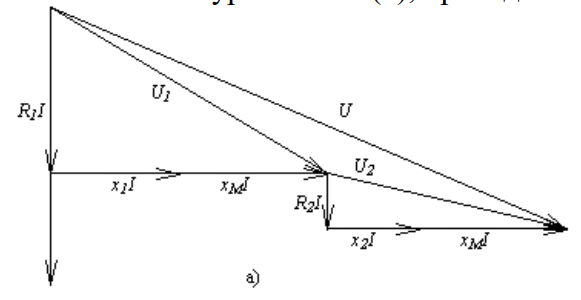
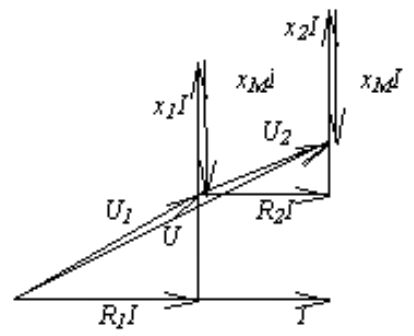
Схема электрической цепи:Рис. 1Векторные диаграммыРис. 2а – согласное включениеРис. 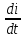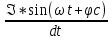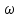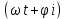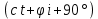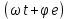2б – встречное включениеСогласное включениеРазобьем диаграмму на две частиПервая часть: Напряжение U_R1 совпадает по фазе с током (для цепи с последовательным соединением чертим относительно I)Напряжение на индуктивности опережает ток на 90 градусов, так как ток одинаковый.Докажем:U_L = L = L = *L*I_m*Cos Для перехода от Cos к Sin +90°= U*l_m*SinУравнение тока L = I_m*Sin 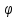_i+ 90 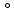и 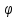_i– действительно опережает на 90°Уравнение по первому закону Кирхгофа:U = R₁*I + j*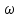*L₁*I + j* 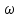*L₂*I + 2*j* 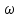*M*I + R₂*IЗнак «+» у слагаемого

---

j* *M*I соответствует согласному включению => х₁*I + х_M*IНапряжение U₁ будет равно сумме векторов R₁*I и x₁*I + х_M*IВо второй части графика всё аналогично. Общее напряжение U будет равно сумме векторов U₁ иU₂ по правилу треугольниковВстречное включениеПри последовательном соединении ток одинаков, поэтому произвольно откладываем вектор I. Напряжение U_R1 совпадает по фазе с током.Напряжение на индуктивности опережает ток на 90° (доказал в предыдущей диаграмме)Уравнение по второму закону Кирхгофа имеет вид:U = R₁*I + j**L₁*I + j* *L₂*I – 2*j* *M*I + R₂*IЗнак «-» у слагаемого j* *M*I соответствует встречному включению x₁*I + х_M*IНапряжение U₁ соответствует сумме векторов R₁*I и x₁*I - х_M*IВторая часть диаграммы выполняется аналогично. 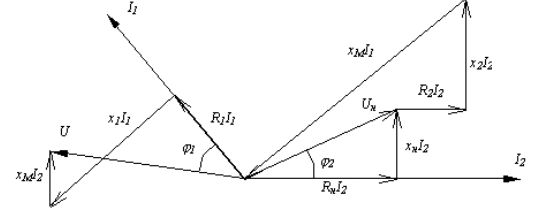Общее напряжение равно геометрической сумме векторов U₁ иU_2.Диаграмма при трансформаторном включении.Рис. 3

---

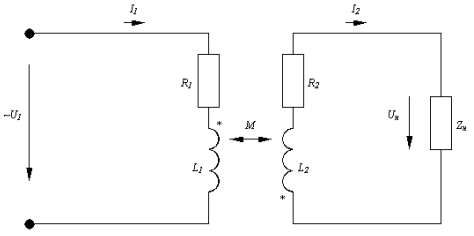
Рис. 4Уравнения, составленные по II закону Кирхгофа для цепей 1-ой и 2-oй катушек: U₁ = (R₁ + j* *L₁)*I₁ + j**M*I₂0 = (R₂ + j* *L₂)*I₂ + j* *M*I₁ + U_нГдеU_н= R_н*I₂ + j*x_н*I₂.Вначале строится вектор тока I₂ вторичной обмоткой произвольным образом. Напряжение на активном сопротивлении R_н*I₂совпадает по фазе с током I₂ (откладываем от начала вектора I₂). Далее откладываем напряжение на индуктивном элементе. Оно опережает ток на 90. U_M получаем из суммы векторов (геометрической)U_M = R_н*I₂ + x_M*I₂. После построения треугольника появляется угол _2, который определяет потери в нагрузке на реактивном сопротивлении. После строим вектор напряжения на индуктивности х₂*I₂ (опережает на 90)Далее проводится вектор х_M*I₁ – вектор напряжения взаимоиндукции на первичной обмотке.Затем проводим вектор тока I₁ = (x_M*I₁) / x_M, который отстает от вектора x_M*L₁ на 90°. С ним по фазе вектора активного сопротивления R₁*I₁, далее строим вектор напряжения на индуктивности x₁*I₁ , который опережает на 90°

---

R₁*I₁ на первичной обмотке. После из конца вектора x₁*I_1, откладываем вектор напряжения взаимоиндукции вторичной обмотки x_M*I₂ , который сонаправлен с вектором x_M*I_2. Из начала координат (начало вектора I₂) откладываем результирующий вектор U, который будет равен напряжению в первичной обмотке.Появился угол ₁, который определяет потери нагрузки на реактивном сопротивлении.ЗаключениеВ ходе данной работы было исследовано включение индуктивно-связных катушек. Какие возможны виды включений и как при этом будет себя вести катушки. Каким образом меняются параметры схем и действующие в ней напряжения и токи. Выводы согласуются с нашими теоретическими представлениями о процессах, происходящих в индуктивных цепях

---

Смотрите также файлы

• Инструкция для радиостанции.pdf

• Комплексные методы получения инженерногеологической информации Инженерногеологическая съемка.pptx

• Реферат По дисциплине Финансовая грамотность На тему Зачет.docx

• Контрольная работа 2 Москва 2023 г.doc

• Практическая работа к теме 6 Человек созидание Выполните следующие действия Перейдите по ссылке на портал Единое содержание общего образования.docx