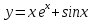Добавлен: 05.12.2023
Просмотров: 15
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра информационных систем
отчет
по лабораторной работе №1
по дисциплине «Системы ППР»
Тема: Минимизация функций одной
переменной в пакете Matlab.
Вариант: 6
| Студент гр. 6373 | | |
| Преподаватель | | |
Санкт-Петербург
2020
Цель работы.
Четырьмя методами найти локальные минимумы следующих функций:
Нахождение минимумов формулы №1
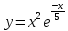
Вид функции на языке Matlab:
function y = fx(x)
y = x.^2.*exp(-1/5*x);
end
Таблица 1 – Нахождение локального минимума
| | Оптимальный пассивный поиск (delta = 0.0001) | Метод деления отрезка пополам (delta = 0.0001) | Метод Фибоначчи (eps = 0.0001) | Метод золотого сечения (eps = 0.0001) |
| X локального минимума | 1.6859e-12 | 0 | 6.2931e-05 | 5.9609e-05 |
| Значение функции в точке минимума | 2.8423e-24 | 0 | 3.9603e-09 | 3.5532e-09 |
Точки минимума получились разные, но они близки друг к другу. Разный результат объясняется погрешностью. Убедимся в правильности найденных точек, построив график функции
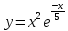(рис. 1).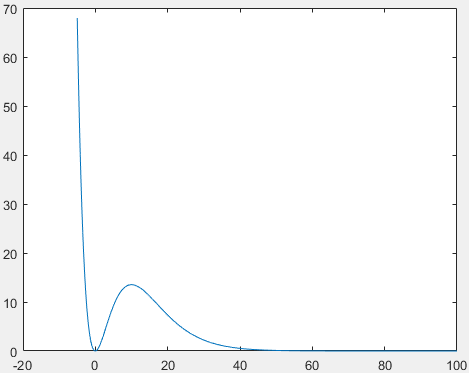
Рисунок 1 – График функции.
Из графика видно, что точки найдены верно.
Нахождение минимумов формулы №2
Вид функции на языке Matlab:
function y = fx(x)
y = x*exp(x)+sin(x);
end
Таблица 2 – Нахождение локального минимума
| | Оптимальный пассивный поиск (delta = 0.0001) | Метод деления отрезка пополам (delta = 0.0001) | Метод Фибоначчи (eps = 0.0001) | Метод золотого сечения (eps = 0.0001) |
| X локального минимума | -1.4633, -7.8513, -14.1372, -2πn | -1.4633, -7.8513, -14.1372, -2πn | -1.4633, -7.8513, -14.1372, -2πn | -1.4633, -7.8513, -14.1372, -2πn |
| Значение функции в точке минимума | -1.3329, -1, -1, …, -1 | -1.3329, -1, -1, …, -1 | -1.3329, -1, -1, …, -1 | -1.3329, -1, -1, …, -1 |
Так как на промежутке [-∞:-2] функция представляет собой синусоиду c периодом 2πn, то у неё бесконечное количество локальных минимумов. Убедимся в правильности найденных точек, построив график функции
(рис. 2).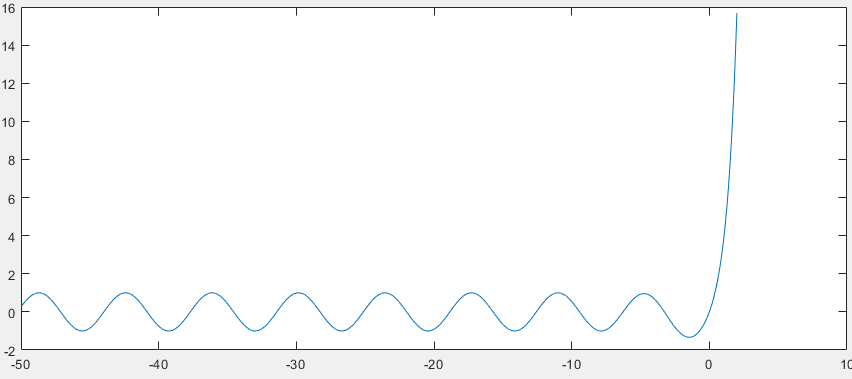
Рисунок 2 – График функции.
Из графика видно, что точки найдены верно.
Выводы.
В данной лабораторной работе были найдены локальные минимумы двух функций с помощью: оптимального пассивного поиска, метода деления отрезка пополам, метода Фибоначчи и метода золотого сечения.
При нахождении локальных минимумов первой функции получилось 4 разных ответа, но они очень близки друг к другу. Эту разницу можно объяснить погрешностью. Полученные результаты были проверены с помощью графика.
Найти все локальные минимумы второй функции невозможно, так как на промежутке [-∞:-2] функция представляет собой синусоиду c периодом 2πn. Полученные результаты были проверены с помощью графика.
ПРИЛОЖЕНИЕ 1
Используемый код
-
Метод оптимального пассивного поиска – Файл passiveSearch.m
function x=passiveSearch(a,b,delta)
%Вход - a - Начало интервала
% - b - Конец интервала
% - delta - Расстояние между точками
%Выход - x - Минимальный локальный минимум
i = a;
min_x = i;
min_y = fx(min_x);
while i<=b
if (min_y > fx(i))
min_x = i;
min_y = fx(min_x);
end
i = i + delta;
end
x = min_x;
end
-
Метод деления отрезка пополам – Файл delotrpopolam.m
function x=delotrpopolam(a,b,delta)
ak=a;
bk=b;
xkc=0;
l2k=bk-ak;
while l2k>delta
%3 этап%
l2k=bk-ak;
xkc=(ak+bk)/2;
Fxkc=fx(xkc);
%4 этап%
yk=ak+l2k/4;
zk=bk-l2k/4;
Fyk=fx(yk);
Fzk=fx(zk);
if Fyk
bk=xkc;
elseif Fzk
ak=xkc
else
ak=yk;
bk=zk;
end
end
x=xkc;
end
-
Поиск по золотому сечнию – Файл goldcut.m
function x=goldencut(a,b,eps,func)
m=1/eps;
d(1)=b-a;
a1=2/(3+sqrt(5));
a2=2/(1+sqrt(5));
alf=a+a1*d(1);
bet=a+a2*d(1);
ak(1)=a;
bk(1)=b;
fa(1)=func(alf);
fb(1)=func(bet);
for i=1:m
if fa(i)>fb(i)
ak(i+1)=alf;
bk(i+1)=bk(i);
d(i+1)=bk(i+1)-ak(i+1);
alf=bet;
bet=ak(i+1)+a2*d(i+1);
fa(i+1)=fb(i);
fb(i+1)=func(bet);
end
if fa(i)<=fb(i)
ak(i+1)=ak(i);
bk(i+1)=bet;
d(i+1)=bk(i+1)-ak(i+1) ;
bet=alf;
alf=ak(i+1)+a1*d(i+1);
fa(i+1)=func(alf);
fb(i+1)=fa(i);
end
epsilon=bet-alf;
if epsilon
break;
end
end
x=(alf+bet)/2;
end
-
Метод фибоначчи –
Файл Fibb.m
function Bn=Fibb(n)
if(n==1)or (n==2)
Bn=1;
end;
if(n==3)
Bn=2;
end;
B(1)=1;
B(2)=1;
for i=3:n+1
B(i)=B(i-1)+B(i-2);
end;
B(n)=B(n+1);
Bn=B(n);
end
Файл MethodFibb.m
function x=MetodFibb(a,b,eps)
m=1/eps;
d(1)=b-a;
n=1;
for i=3:m
B=Fibb(i);
a1=d(1)/B;
if a1>eps
n=i-1;
end;
end;
alf=a+d(1)*Fibb(n-1)/Fibb(n+1);
bet=a+d(1)*Fibb(n)/Fibb(n+1) ;
fa(1)=fx(alf);
fb(1)=fx(bet);
ak(1)=a;
bk(1)=b;
for i=1:n
k=i-1;
k0=n-k;
k1=k0-1;
k2=k0+1;
if fa(i)>fb(i)
ak(i+1)=alf;
bk(i+1)=bk(i);
d(i+1)=bk(i+1)-ak(i+1);
alf=bet;
bet=ak(i+1)+d(i+1)*Fibb(k0)/Fibb(k2);
fa(i+1)=fb(i);
fb(i+1)=fx(bet);
end;
if fa(i)<=fb(i)
ak(i+1)=ak(i);
bk(i+1)=bet;
d(i+1)=bk(i+1)-ak(i+1);
bet=alf;
alf=ak(i+1)+d(i+1)*Fibb(k1)/Fibb(k2);
fa(i+1)=fx(alf);
fb(i+1)=fa(i);
end;
epsilon=bet-alf;
if epsilon
break;
end;
end;
x=(alf+bet)/2;
end