Федеральное государственное образовательное бюджетное учреждение высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-Бруевича»

____________________________________________________________________________

Кафедра радиосистем и обработки сигналов

Дисциплина «Цифровая обработка сигналов»

Лабораторная работа ЛР07

ДИСКРЕТНЫЕ СИГНАЛЫ

Выполнили:

Великоборец Антон

Теровец Алексей

Группа:

ИКТЗ-15

Проверил:

Гуреев А.Е.

Санкт-Петербург

2023

Отчет

Исходные данные

Перемен ная	Назначение	Значение	Идентификатор
Nбр	Номер бригады	Nбр	Nb = 10
N	Длина последовательности	N= +30 Nбр mod5	N = 30
T	Период дискретизации	T= 0,0005(1+Nбр mod3)	T = 0.001
a	Основание экспоненты	a= −( 1)Nбр (0,8+0,005Nбр)	a = 0.85
C	Амплитуда гармонического сигнала	C= 1+ Nбр mod5	С = 1
ωˆ0(рад)	Частота гармонического сигнала		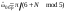w0 = pi/6
m	Задержка	m= 5+ Nбр mod5	m = 5
U	Амплитуда импульса	U =N бр	U = 10
n0	Начальный момент импульса	n 0 = Nбр mod 5+ 3	n0 = 3
nimp	Длина импульса	nimp =Nбр mod 5+5	n_imp = 5
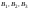	Амплитуды гармонических сигналов	B1 = +1,5 Nбр mod5 B2 = 5,7 −Nбр mod5 B3 = 2,2 +Nбр mod5	Вектор B = [1.5 5.7 2.2]
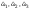	Частоты гармонических сигналов		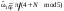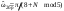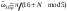Вектор w = [pi/4 pi/8 pi/16]
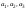	Коэффициенты линейной комбинации гармонических сигналов		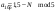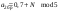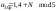Вектор A = [1.5 0.7 1.4]
mean	Математическое ожидание	mean =Nбр mod 5+ 3	Mean = 3
var	Дисперсия	var =Nбр mod 5+ 5	Var = 5

---

Пункты задания

п.1. ЦИФРОВОЙ ЕДИНИЧНЫЙ ИМПУЛЬС ????₀(????????) (идентификатор u₀)



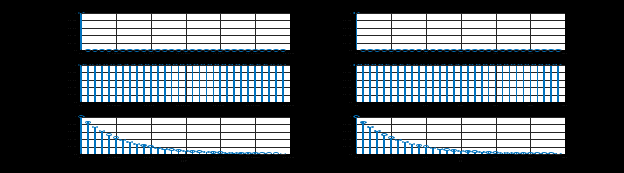
Пояснение:

Взаимосвязь между дискретным и дискретным нормированным временем:

Дискретным временем называют значения , где — период дискретизации. Дискретным нормированным временем называют значения : . В этом случае формально , имеет смысл номера отсчёта, а значения отсчетов остаются неизменными: .

Различие между цифровым единичным импульсом и дельта-функцией:

Цифровой единичный импульс — это аналог дельта-импульса для дискретных систем, но в отличие него – физически реализуемый сигнал. Подобно дельта-импульсу, цифровой единичный импульс обладает фильтрующим свойством: из бесконечной последовательности выделяется один отсчёт в текущий момент времени n.

Дельта-функция (она же функция Дирака), используется в аналоговых системах

Формула дельта-функции.

???? =



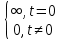
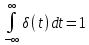
Эта функция бесконечно малой длительности, с бесконечным значением и площадью 1.

п.2. ЦИФРОВОЙ ЕДИНИЧНЫЙ СКАЧОК

---

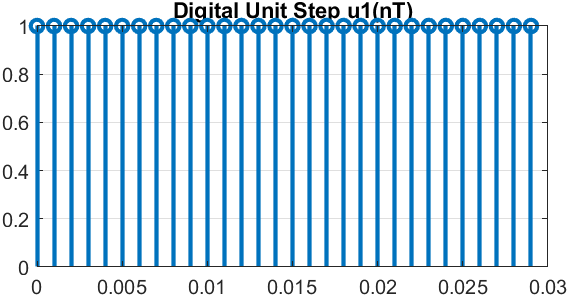
Пояснение:

Соответствие между цифровым и аналоговым единичными скачками:

Функция единичного скачка (она же функция Хевисайда, или функция включения), используется в аналоговых системах.

Скачки не задержаны. Аналоговый является для цифрового скачка огибающей.

Чему равна частота дискретизации цифрового единичного скачка.



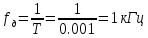
п.3. ДИСКРЕТНАЯ ЭКСПОНЕНТА



Пояснение:

Соответствие между дискретной и аналоговой экспонентами.

Вид дискретной экспоненты определяется величиной и знаком параметра a.

Формула дискретной экспоненты в общем виде и со своими исходными данными.

????(????) = , ????(????) =

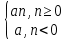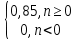
п.4. ДИСКРЕТНЫЙ КОМПЛЕКСНЫЙ ГАРМОНИЧЕСКИЙ СИГНАЛ





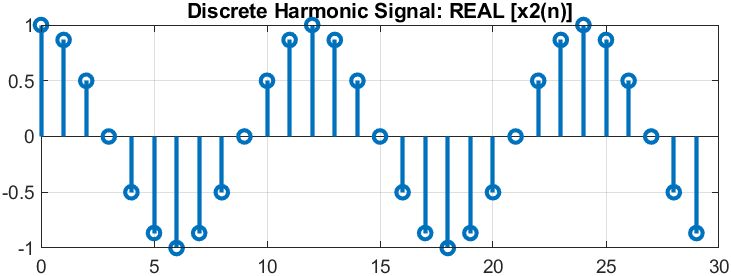
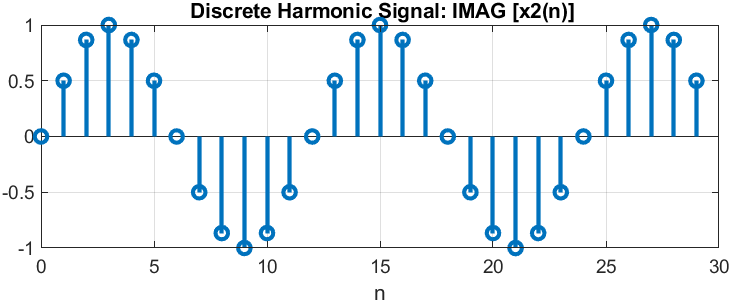
Пояснение:

Сигнал в виде комбинации двух вещественных последовательностей.

????(????????) = ????(????) = ????????????????????????;

????(????) = ????????????????(????????????) + ????????????????????(????????????);





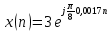
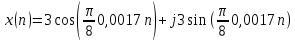
п.5. ЗАДЕРЖАННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ



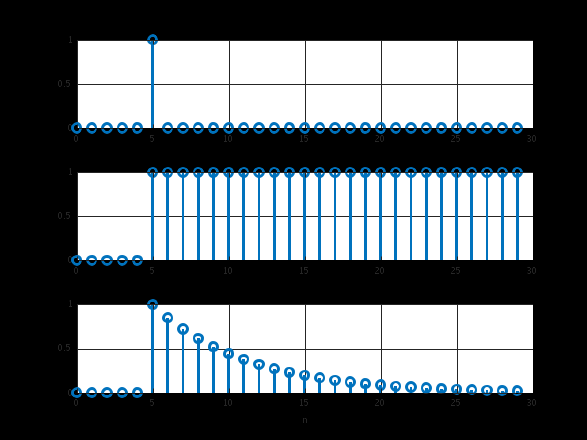
Пояснение:

????₀(???? − ????) = 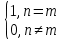; ????1(???? − ????) = ; ????(???? − ????) =

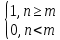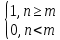
п.6. ДИСКРЕТНЫЙ ПРЯМОУГОЛЬНЫЙ ИМПУЛЬС

---

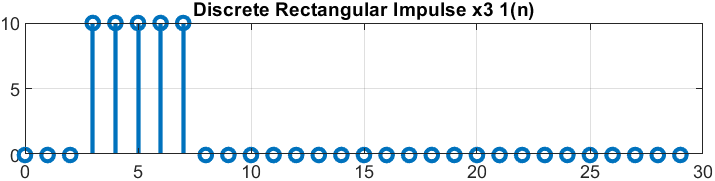
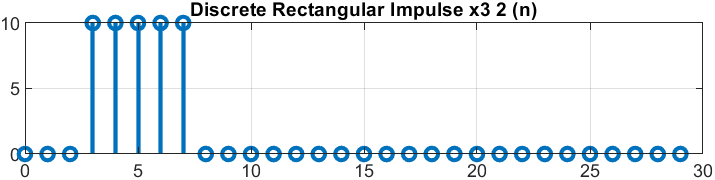
Пояснение:

y = rectpuls(t,w), где

y — вектор значений прямоугольного импульса с единичной амплитудой, центрированного относительно t = 0;
t – вектор значений времени,
w – ширина (длительность) импульса.

Функция rectpuls формирует отсчеты одиночного прямоугольного импульса с единичной амплитудой, вычисленные для моментов времени, заданные входным вектором t. Этот импульс центрирован относительно момента времени t = 0 и по умолчанию имеет единичную длительность.

п.7. ДИСКРЕТНЫЙ ТРЕУГОЛЬНЫЙ ИМПУЛЬС



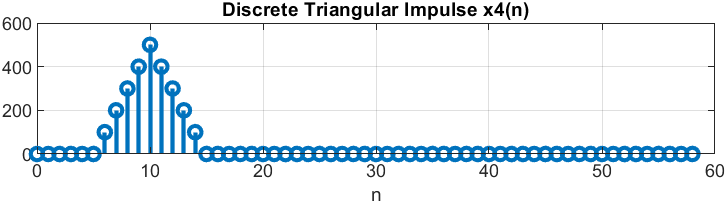
Пояснение:

Аналитическая запись свёртки.



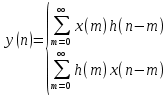
п.8. ЛИНЕЙНАЯ КОМБИНАЦИЯ ДИСКРЕТНЫХ ГАРМОНИЧЕСКИХ СИГНАЛОВ

• 
  Средние значение mean_x5 = 0.28396
  
• 
  Энергия E = 2231.4742
  
• 
  Средняя мощность P = 14.8765
  

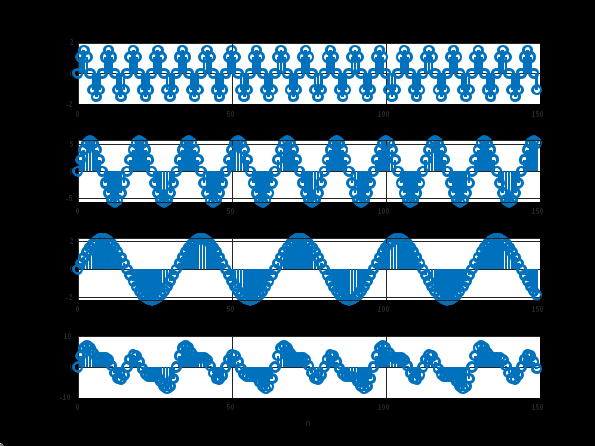
Пояснение:

При моделировании сигналов использована операция сложение сигналов - sum.

Среднее значение: mean(x)

Энергия: sum(x.^2)

Средняя мощность: sum(x.^2)/length(x) , где lenghth(x) – длина последовательности.

п.9. ДИСКРЕТНЫЙ ГАРМОНИЧЕСКИЙ СИГНАЛ С ЭКСПОНЕНЦИАЛЬНОЙ ОГИБАЮЩЕЙ



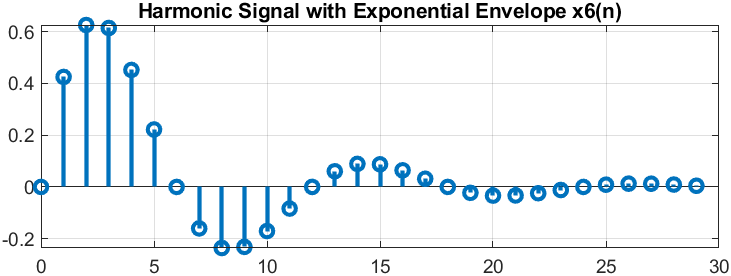
Пояснение:

Аналитическая формула дискретного сигнала ????₆(????):



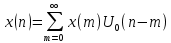
п.10. ПЕРИОДИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ДИСКРЕТНЫХ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ



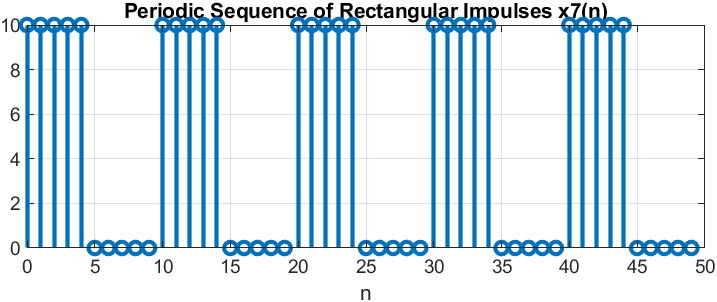
Пояснение:

Операции при моделировании периодической последовательности;

y=square(t,d) , где d — параметр, определяющий длительность положительной полуволны в процентах от периода (по умолчанию d=50); а остальные параметры

определены в функции rectpuls.

п.11. РАВНОМЕРНЫЙ БЕЛЫЙ ШУМ



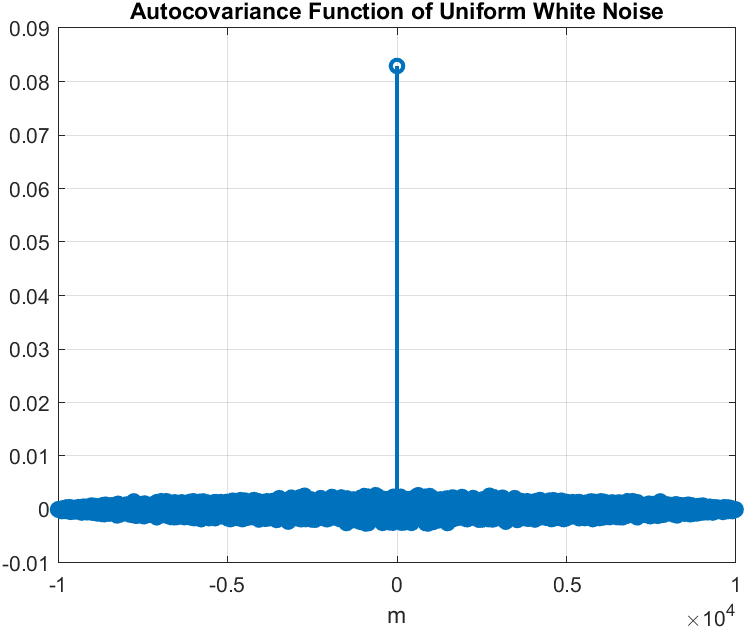
Пояснение:

Чему равны истинные значения математического ожидания и дисперсии.

---

M(x)= 0.49956; D(x)=0,08291

Каков вид истинной автоковариационной функции.

Автоковариационная функция имеет цифрового единичного скачка

Чему равна длина оценки автоковариационной функции.

Длина оценки: L=2N-1

Формула автоковариационной функции



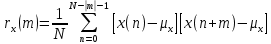
Позволяет оценить зависимость между отклонениями отсчетов последовательности от среднего значения ???????? при различных сдвигах по времени m.

п.12. НОРМАЛЬНЫЙ БЕЛЫЙ ШУМ



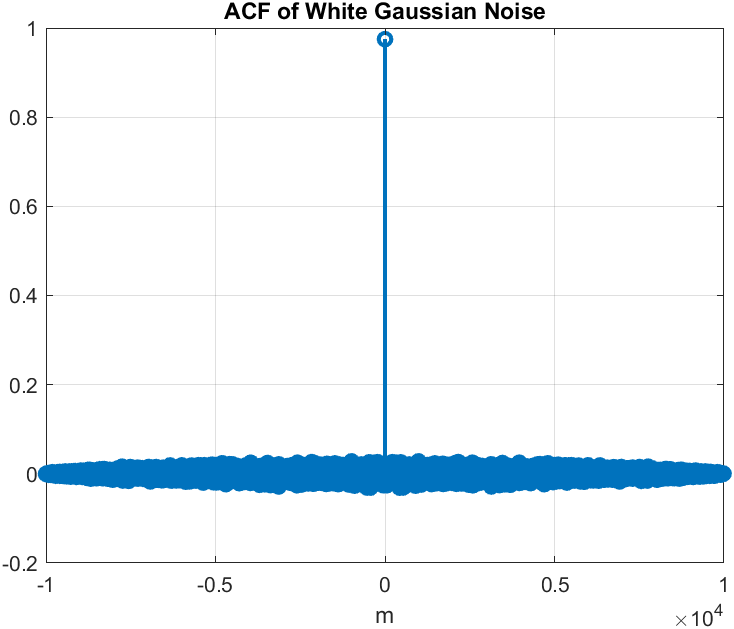
Пояснение:

Чему равны истинные значения математического ожидания и дисперсии. M(x)=0,0018848; D(x)=0,97502

Каков вид истинной АКФ.

АКФ имеет вид цифрового единичного скачка.

Чему равна длина оценки АКФ.

L=2N-1

АКФ позволяет оценить зависимость между её отсчётами при различных сдвигах по времени m:



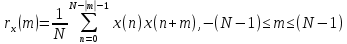
п.13. АДДИТИВНАЯ СМЕСЬ ДИСКРЕТНОГО ГАРМОНИЧЕСКОГО СИГНАЛА С НОРМАЛЬНЫМ БЕЛЫМ ШУМОМ



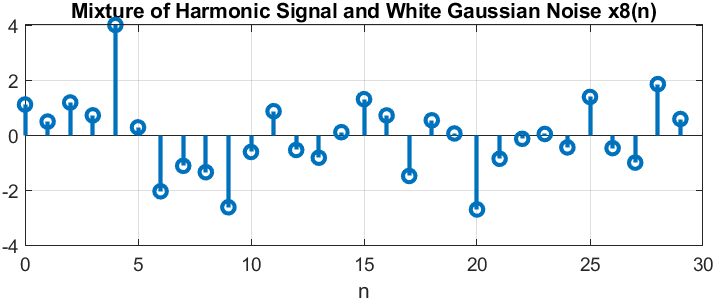
Пояснение:

Аддитивная смесь сигнала с шумом – суммируется шум с полезным сигналом.

п.14. ОЦЕНКА АКФ ПОСЛЕДОВАТЕЛЬНОСТИ С ВЫВОДОМ ГРАФИКА АКФ


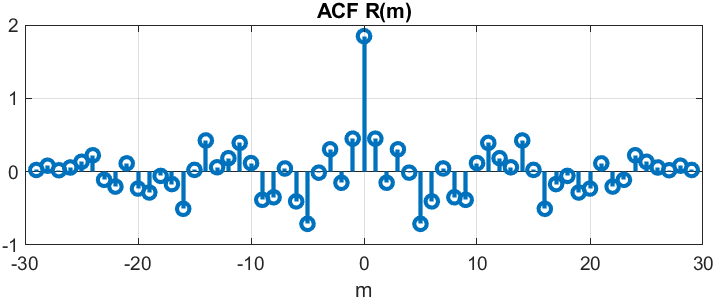
Пояснение:

• 
  Дисперсия var_x8 = 1.9112
  
• 
  R(N) = 1.8475
  

Свойства АКФ.

Являются чётными функциями длины L=2N-1, центрированными относительно m=0:

????_????(????) = ????_????(−????) ????_????(????) = ????_????(−????)

при ????_???? = 0 получаем равенства:

????_????(????) = ????_????(????)

????_????(0) = ????_????(0) = ????²_????

П.15. НОРМАЛЬНЫЙ БЕЛЫЙ ШУМ С ЗАДАННЫМИ СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ



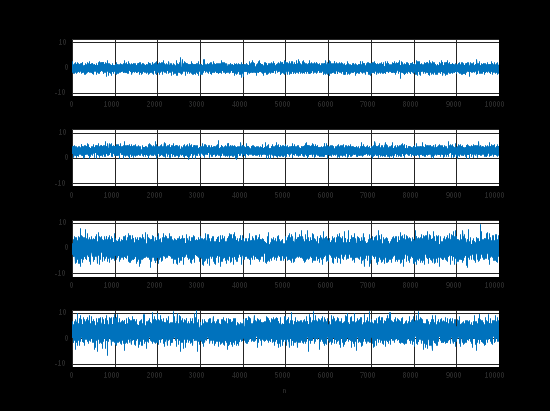
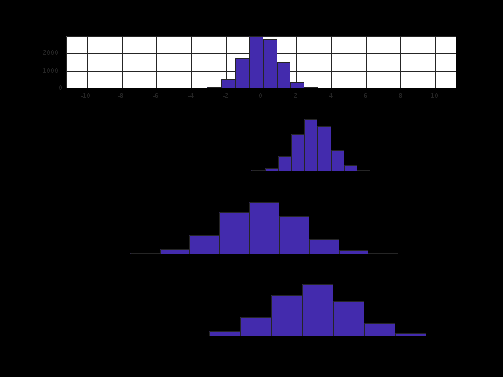
Пояснение:

К каким изменениям шума приводит изменение его математического ожидания и дисперсии.

---

Смотрите также файлы

• Актуальность темы обусловлена тем, что для большинства российских предприятий маркетинговое управление становится одним из условий выживания и успешного функционирования.rtf

• Физические основы применения лазерной техники в медицине.rtf

• Отчет по лабораторной работе 4 по дисциплине Защита информации в системах беспроводной связи.docx

• Название способа.docx

• Федеральное государственное образовательное бюджетное учреждение высшего образования финансовый университет.pdf