Файл: Курсовая работа по дисциплине Теория и методы принятия решений.docx
Добавлен: 05.12.2023
Просмотров: 71
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Кафедра АСОиУКурсовая работа по дисциплине
«Теория и методы принятия решений»
Вариант 4.9
Выполнил: Агапитов В.Ю.
группа: 1362
Проверила: Матевицкая Н.Е.
2014
Санкт-Петербург
Задача 1
В сельхозобъединении предполагается выращивать четыре вида кормовых культур. Урожайность культур можноувеличить за счет внесения удобрений.Урожай кормовых культурК-1, K-2, K-3 снимается два раза в год, урожай культуры К-4 снимается три раза в год. Соответственно удобрения вносятся для кормовых культур К-1, K-2, K-3 два раза в год, для культуры К-4 - три раза в год. Урожайность по различным культурам не зависит от участка посева; ее зависимость от количества Х внесенных удобрений может быть аппроксимирована выражением
Y = Ф(Х) [ц/га] ;
функция остатка за период подкормки имеет вид f(X)=dX. Количество удобрений на один год составляет К единиц и распределяется пропорционально плану производства кормовых культур. Годовой план по кормовым культурам К-1, K-2, K-3, K-4, составляющий P1, P2, P3, P4 [т] соответственно, а также значения параметров функций Ф(X), f(X) (коэффициентов a, b, c, d) приведены в табл. 1. Требуется найти оптимальный план внесения удобрений для повышения урожайности кормовых культур.
Ф(X) K
a-b*e^(-cX) 120
Таблица 1
iКультураabcdP
1 K-1 30 10 2 .7 1000
2 K-2 50 12 3 .8 1500
3 K-3 40 10 2 .75 2000
4 K-4 38 12 4 .1 600
Решение:
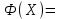- функция дохода (эффективности)K=120 - количество ресурса
Определим количество удобрений, приходящихся на долю каждой культуры т.к. количество удобрений на год распределяется пропорционально плану производства кормовых культур.
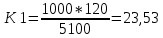; К2 = 35,29; К3 = 47,06; К4 = 14,12Формула для подсчета урожайности в зависимости от удобрений:
Fn(x) =
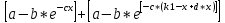, 0≤x≤KnУрожайность первой культуры
F1(x) =
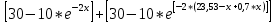, 0≤x≤23,53Получим вот такой график:
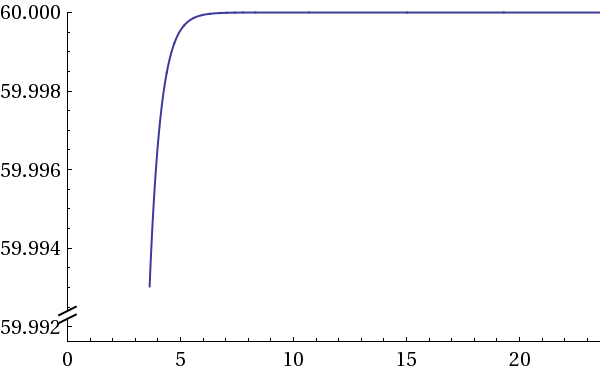
F1(x)
x
1.1 График урожайности первой культуры
Максимум функции достигается при х=18,56 и равняется F1(x)=60.
Вывод:
Оптимальный план внесения удобрений для повышения урожайности первой кормовой культур - это 18,56 единиц, что даст нам максимальную урожайность равную 60 ц/га.
Урожайность второй культуры
F2(x) =
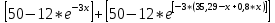, 0≤x≤35,29Получим вот такой график:
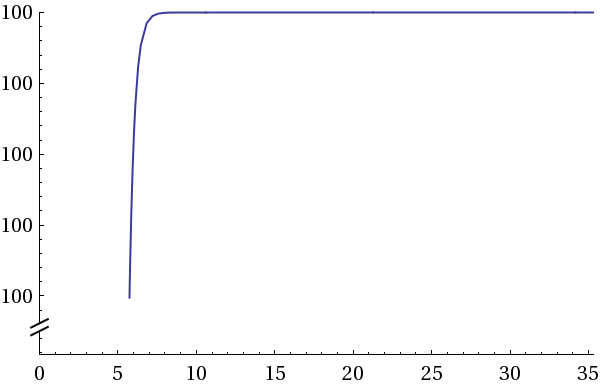
F2(x)
x
1.2. График урожайности второй культуры
Максимум функции достигается х=29,86 и равняется F2(x)=100.
Вывод:
Оптимальный план внесения удобрений для повышения урожайности второй кормовой культур - это 29,86 единиц, что даст нам максимальную урожайность равную 100 ц/га.
Урожайность третьей культуры
F3(x) =
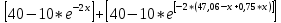, 0≤x≤47,06Получим вот такой график:
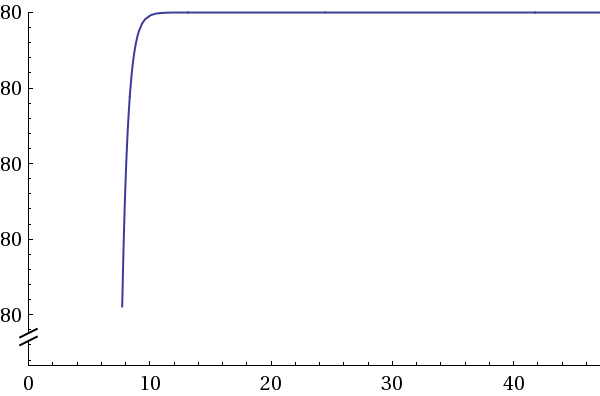
F3(x)
x
1.3. График урожайности третей культуры
Максимум функции достигается х=38,20 и равняется F3(x)=80.
Вывод:
Оптимальный план внесения удобрений для повышения урожайности второй кормовой культур - это 28,20 единиц , что даст нам максимальную урожайность равную 80 ц/га.
Урожайность четвертой культуры
Имеющиеся у нас ресурсы для четвёртой культуры распределяются на трёх этапах, при начальной величине ресурса
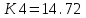, с возможностью частичного резервирования на последующих этапахПроцесс описывается однородными функциями.
; 
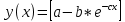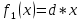, где d=0.1;Для отражения возможности резервирования ресурса введем второй, фиктивный процесс:
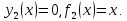
Обратная прогонка
Этап 3
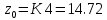– начальное значение ресурса.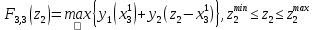
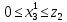
где
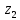– количество имеющихся ресурсов (удобрений) на данном этапе.В данном случае, остаток от второго (фиктивного) процесса превышает остаток от первого процесса, поэтому пределы возможных изменений текущих величины ресурса
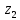вычисляются: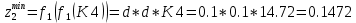
Таким образом:
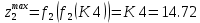
Состояние рассматриваемой системы, состоящей из двух процессов, в каждый момент времени описывается величинами:
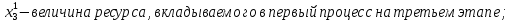
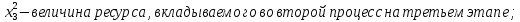
Которые обобщенно обозначаются величиной
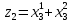т.к.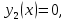 
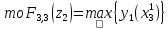
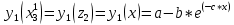
где a=38, b=12, c=4, d=0.1, K4=14.72
График урожайности на этапе 3:
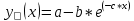
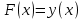
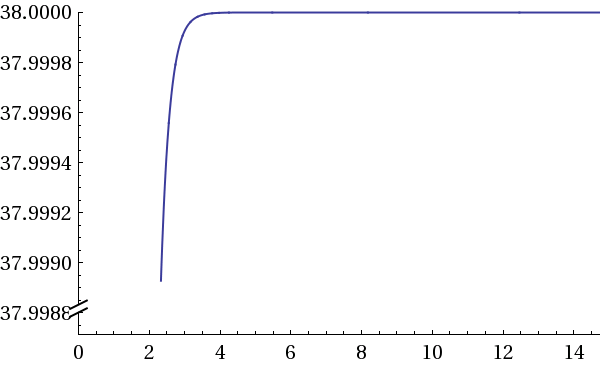
Рис. 1.4.
x
F(x)
Этап 2
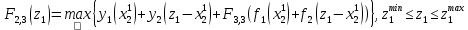
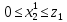
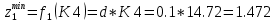
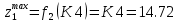
т.к.
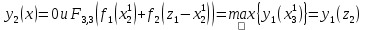
то
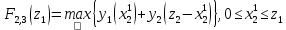
График урожайности на этапе 2:
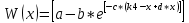
+W(x);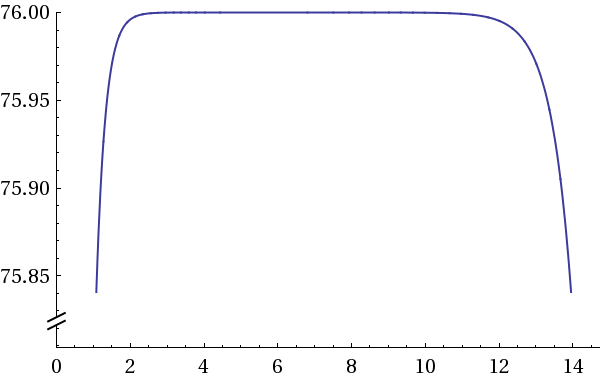
F(x)
x
Рис. 1.5.
Этап 1
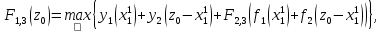
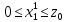
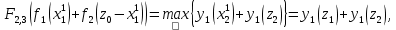
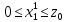
то
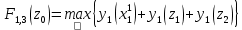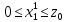
, График урожайности на этапе 1:
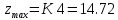
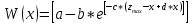
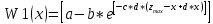
+W(x)+W1(x);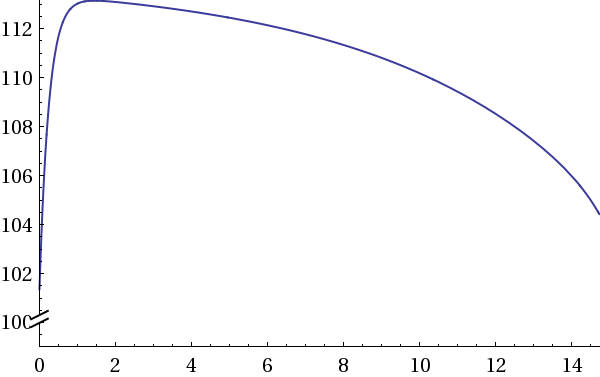
F(x)
x
Рис. 1.6. График урожайности четвертой культуры
Вывод
Оптимальный план внесения удобрений для повышения урожайности четвертой кормовой культур это 1,45 единиц, что даст нам максимальную урожайность равную 113,14 ц/га.
Задача 2
Для посева этих культур используются три участка посевных площадей размером S1, S2, S3 [га]. Характеристики себестоимости [руб/т] выращивания тонны i-й культуры на j-м участке, а также площади участков представлены в табл.2.Требуется найти план посева (распределения культур по участкам), оптимальный с точки зрения минимизации себестоимости, и провести исследование решения:
а) при условии минимума затрат выяснить возможности дополнительного посева культур с полным использованием площадей участков
;
б) выяснить размер свободных площадей на участках при точном выполнении планов;
в) применяя средства параметрического исследования правых частей, провести постепенное увеличение планов (по возможности, до заполнения участков);
г) сравнить результаты пп. "а" и "в".
Таблица 2
j 1 2 3 Участки
1 K-1 40 50 30
2 K-2 35 30 50
3 K-3 45 60 35
4 K-4 25 50 40
S 600 800 1000
Решение:
Пусть i-номер культуры, соответственно
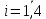, аj-номер участка и 
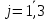.Тогда составим систему ограничений и запишем целевую функцию.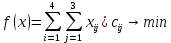
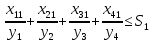
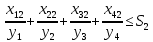
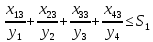
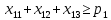
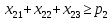
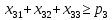
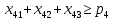
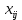– количество i-йкультуры,засеянной на j-м участке.
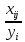– доляi-й культуры на j-м участке.
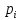– план по сбору i-й культуры.
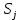- площадь j-го участка.
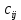– затраты на выращивание i-й культуры на j-м участке.f(x)– целевая функция.
Где,
Табличная форма записи данных
А)
| | Х11 | Х12 | Х13 | Х21 | Х22 | Х23 | Х31 | Х32 | Х33 | Х41 | Х42 | Х43 | Т.О. | П.ч. |
| Z | 40 | 50 | 30 | 35 | 30 | 50 | 45 | 60 | 35 | 25 | 50 | 40 | Min | |
| Y1 | 1 | 1 | 1 | | | | | | | | | | ≥ | 1000 |
| Y2 | | | | 1 | 1 | 1 | | | | | | | ≥ | 1500 |
| Y3 | | | | | | | 1 | 1 | 1 | | | | ≥ | 2000 |
| Y4 | | | | | | | | | | 1 | 1 | 1 | ≥ | 600 |
| Y5 | 0.17 | | | 0.1 | | | 0.125 | | | 0.088 | | | ═ | 600 |
| Y6 | | 0.17 | | | 0.1 | | | 0.125 | | | 0.088 | | ═ | 800 |
| Y7 | | | 0.17 | | | 0.1 | | | 0.125 | | | 0.088 | ═ | 1000 |