Файл: Отчет по лабораторной работе определение линейных величин и углов.doc
Добавлен: 05.12.2023
Просмотров: 233
Скачиваний: 23
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
| |
| (наименование отделения / школы) |
| |
| (направление / специальность) |
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ
| ОПРЕДЕЛЕНИЕ ЛИНЕЙНЫХ ВЕЛИЧИН И УГЛОВ |
| (номер / название лабораторной работы) |
| Вариант: | 1 |
| (номер вашего варианта) | |
| Дисциплина: | Физика |
| | (наименование дисциплины) |
| Студент: | | Каюмов Ш.О. | 21.04.23 |
| | (номер группы) | (фамилия, инициалы) | (дата сдачи) |
| Руководитель: | | | |
| | (должность, уч. степень, звание) | (фамилия, инициалы) | |
| Томск – | 2023 |
| (город, год) | |
Краткое теоретическое содержание работы
| Нониус – это ... | |
| Дополнительная линейка с делениямии, которая может перемещаться вдоль шкалы | |
| Точность нониуса определяется по формуле | |
| x=y/m | |
| где | |
| y – | Расстояние между соседними штрихами масштаба |
| m – | Число делений нониуса |
Расчетные формулы
| Vп = | a·b·c | |
| где | ||
| a – | Длина параллелепипеда | |
| b – | Ширина параллелепипеда | |
| c – | Высота параллелепипеда | |
| Vц = | (πd2/4)*h | |
| где | ||
| D – | Диаметр цилиндра | |
| h – | Высота цилиндра | |
| π – | Математическая постоянная, равная отношению длины окружности к её диаметру (3,14) | |
Схема установки
| Для измерения линейных величин в данной работе используются приборы: | |
| Штангенциркуль и микрометр | |
| основными частями которых являются шкала, называемая масштабом, и нониус:  где | |
| 1 – | масштаб |
| 2 – | нониус |
| Точность нониуса для штангенциркуля, используемого в данной лабораторной работе, равна | |
| 0.1 мм | |
| где | |
| y = | 0,5 мм |
| m = | 50 |
| Длина L отрезка, измеряемая прибором, имеющим нониус, равна  ,где | |
| k – | Целое число деления масштаба, измеряемого тела |
| n – | Ближайшие к делению масштаба деление нониуса |
| | |
| Нониус микрометрического винта (конический нониус) микрометра, используемого | |||
| в лабораторной работе, представляет собой барабан с | 50 | делениями. | |
| Точность нониуса микрометра – | 0,01 | мм. | |
Измерения
| Различают два вида измерений: | ||
| а) прямые – | Измерения, полученные с помощью различных измерительных приборов | |
| б) косвенные – | Измерения, полученные с помощью формул | |
| Различают три вида ошибок: | ||
| а) систематические – | Ошибки, сохраняющие величину и знак от опыта к опыту, проводящиеся в одинаковых условиях | |
| б) приборные – | Ошибки, зависящие от точности измерения величины каким-либо прибором | |
| в) случайные – | Ошибки, изменяющие свою величину или знак от опыта к опыту | |
Результаты измерений линейных размеров тел
Таблица 1
| № | a (мм) | аi(мм) |  | b (мм) | bi (мм) |  | c(мм) | ci (мм) |  |
| 1 | 31,60 | 0,15 | 0,0225 | 19,10 | 0,48 | 0,2304 | 11,35 | -0,02 | 0,0004 |
| 2 | 31,85 | -0,1 | 0,01 | 19,90 | -0,32 | 0,1024 | 11,40 | -0,07 | 0,0049 |
| 3 | 31,70 | 0,05 | 0,0025 | 19,95 | -0,37 | 0,1369 | 11,35 | -0,02 | 0,0004 |
| 4 | 31,80 | -0,05 | 0,0255 | 19,85 | -0,27 | 0,0729 | 11,30 | 0,03 | 0,0009 |
| 5 | 31,80 | -0,05 | 0,0025 | 19,10 | -0,48 | 0,2304 | 11,25 | 0,08 | 0,0064 |
| среднее значение | 31,75 | | | 19,58 | | | 11,33 | | |
Примечание:
, 
, 
, 
;где
, 
, 
– средние значения измеряемых величин a, b, c соответственно.Таблица 2
| № | D(мм) | Di (мм) |  | h(мм) | hi (мм) |  |
| 1 | 22,90 | -0,12 | 0,0144 | 11,75 | -0,08 | 0,0064 |
| 2 | 22,50 | 0,28 | 0,784 | 11,65 | 0,02 | 0,0004 |
| 3 | 22,95 | -0,17 | 0,0289 | 11,60 | 0,07 | 0,0049 |
| среднее значение | 22,78 | | | 11,67 | | |
Примечание:
, 
, 
;где
, 
– средние значения измеряемых величин D, h соответственно.Обработка результатов измерений
длины, ширины и высоты параллелепипеда.
Погрешности измерений
| Среднеквадратичная ошибка σx измеряемой величины x (длины, ширины либо высоты) параллелепипеда для случая 5-тикратного измерения величины рассчитывается по формуле | ||
| Δσx = |  | |
| Где | ||
 – |  | |
 – | Среднеарифметическое значение | |
| Случайная погрешность Δxсл измеряемой величины x рассчитывается по формуле | |||
| Δxсл = |  | ||
| Где | |||
| σx – |  | ||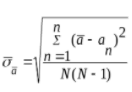
| tα,n — коэффициент Стьюдента для n = 5, α = 0,95 , tα,n = | 2,78 | ||
| Погрешность Δxои однократного измерения величины x рассчитывается по формуле | ||
| Δxои = |  | |
| где | ||
| α – | 0,95 | |
| lx – | 0,05 | |
| Общая погрешность Δx измеряемой величины x рассчитывается по формуле | ||
| Δx = |  | |
| где | ||
| Δxсл — |  | |
| Δxои — |  | |
| Относительная погрешность δ определяемой величины объёма параллелепипеда Vп рассчитывается по формуле | |
| δ = |  |
| Абсолютная погрешность ΔVп определяемой величины объёма параллелепипеда Vп рассчитывается по формуле | |
| ΔVп = |  |