При описании Т-волн в линиях передачи можно однозначно ввести понятия напряжения 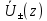и тока 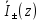и измерить эти величины.

Отношение 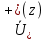к 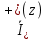падающей бегущей волны (или взятое со знаком минус отношение 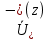к 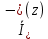отраженной бегущей волны) называют волновым сопротивлением линии передачи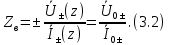



Волновое сопротивление 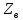отличается от характеристического сопротивления 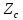и зависит от геометрических параметров поперечного сечения линии передачи и свойств заполняющего линию диэлектрика.

Коэффициент стоячей волны в линии передачи с волной класса Т равен отношению максимальной амплитуды результирующего напряжения в линии к минимальной амплитуде этого напряжения:



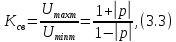
где 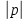 – модуль коэффициента отражения по напряжению.

В режиме бегущей падающей волны 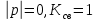. В режиме короткого замыкания или холостого хода .

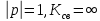В остальных случаях существует смешанный режим, характеризуемый значениями .
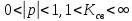Моделирование.

1). Создать новый проект Ansys HFSS.

2). В меню HFSS выбрать пункт Solution Type и выбрать Terminal.

3). Создать представленную на рис. 3.3 микрополосковую линию

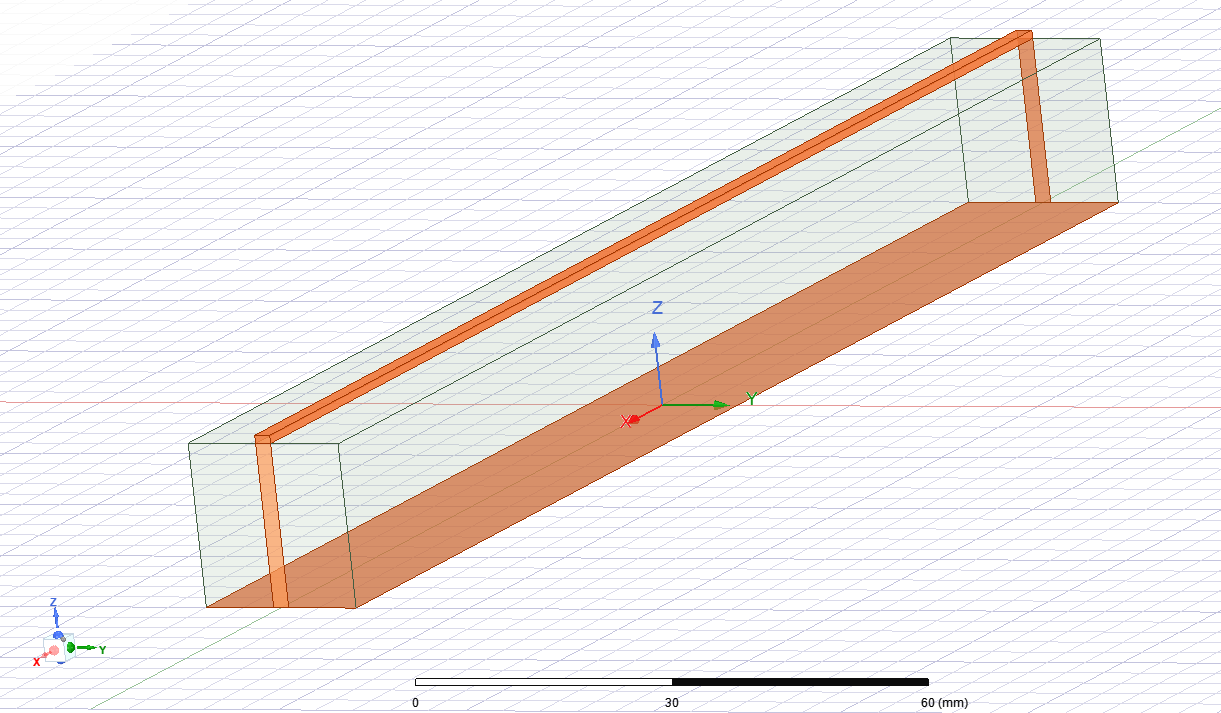Рис. 3.3. Вид микрополоской линии

Прозрачным прямоугольником с размерами 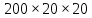является диэлектрик FR4, нижняя пластина является идеальным проводником, а проводящая линия является проводником из меди (copper в библиотеке материалов программы).

---

4). Для корректной работы программы необходимо выполнять следующий порядок создания модели:

а) создать параллелепипед с необходимыми размерами;

б) выбрать нижнюю сторону, создать на ней новый объект с помощью меню Modeler, Surface, Create Object From Face и назначить его как Perfect E;

в) создать линию посередине верхней поверхности параллелепипеда, выбрать тип линии Line, ширину линии 2мм и, с помощью меню Modeler, Surface, Thicken sheet назначить высоту проводника -1мм (при выборе положительной толщины проводник углубится в диэлектрик);

г) с помощью клавиши E перейти в режим выбора граней объектов и выбрать грани с зажатой клавишей Ctrl как показано на рис. 3.4;

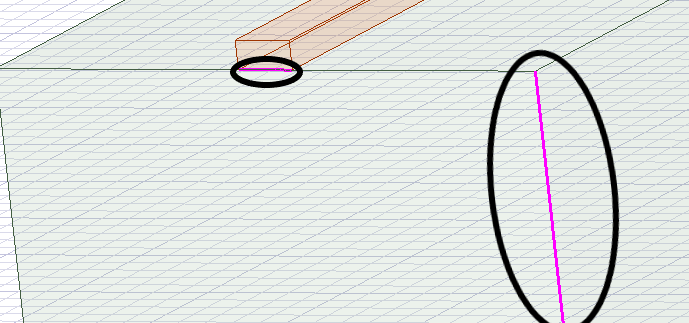Рис. 3.4. Выбор граней для создания питания линии

д) при выбранных гранях выбрать меню Modeler, Edge, Create Object From Edge;

e) в окне Model выбрать полученные объекты и использовать меню Draw, Sweep, Along Path.

ж) назначить Lumped Port и повторить операции по созданию порта для второй стороны микрополосковой линии.

з) сохранить проект.

5). Скопировать проект и сохранить его в другой папке.

6). На основе микрополосковой линии собрать симметричную полосковую линию, представленную на рис. 3.5.

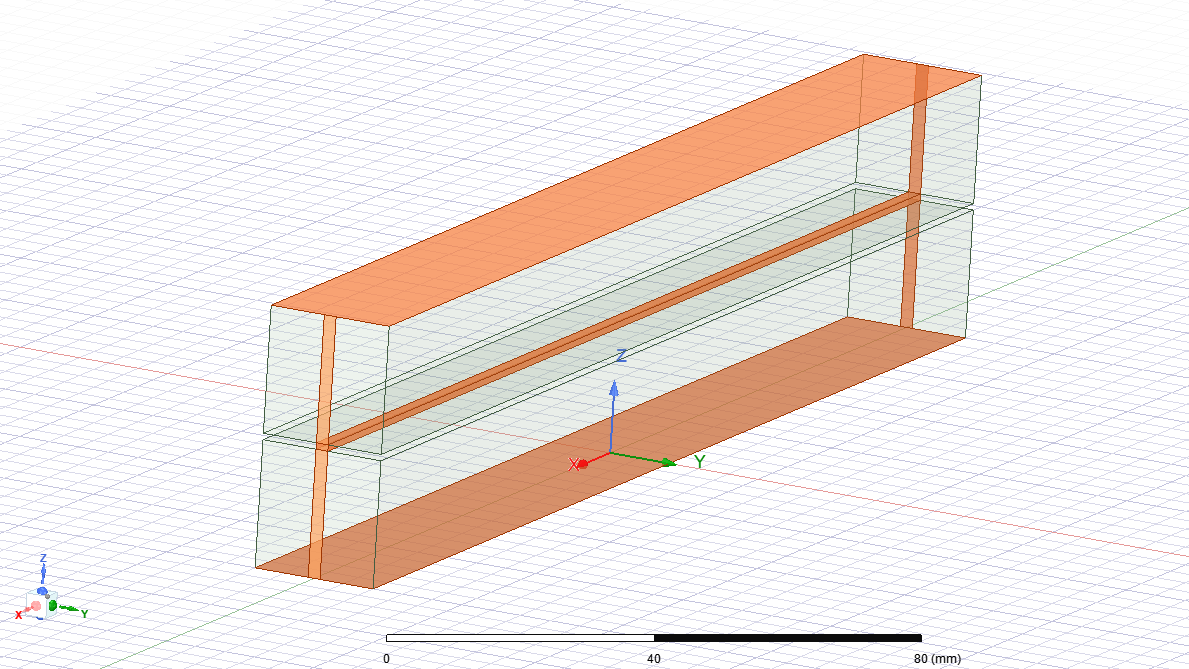Рис. 3.5. Вид симметричной полосковой линии

7). Получить зависимости КСВН от частоты, приложить их к отчету.

Содержание отчета

1. 
   Графическое изображение структуры поля бегущей волны в микрополосковой линии.
   
2. 
   Результаты моделирования.
   

Контрольные вопросы

1. 
   В каких линиях передачи могут распространяться T-волны?
   
2. 
   Как рассчитать диапазон длин волн одноволнового режима?
   
3. 
   Что такое характеристическое сопротивление среды для T-волны?
   
4. 
   Что такое волновое сопротивление линии передачи для T-волн?
   
5. 
   Что такое коэффициент отражения по напряжению?
   

Лабораторная работа 4

---

Исследование характеристик нерегулярных элементов прямоугольном волноводе

Цель работы

1). Исследование влияния различных нерегулярных элементов в прямоугольном волноводе.

2). Расчет теоретических зависимостей от частоты коэффициента стоячей волны (КСВ) исследуемых нерегулярных элементов.

3). Сопоставление результатов моделирования и теоретических расчетов.

Методические указания к самоподготовке

При подготовке к выполнению лабораторной работы необходимо изучить основные свойства и параметры исследуемых нерегулярных элементов в прямоугольном волноводе [1].

Следует обратить внимание на то, что в прямоугольном волноводе на нерегулярном элементе возникает сложное электромагнитное поле, состоящее в общем случае из трех бегущих волн основного типа (падающей от генератора, отраженной нерегулярным элементом и прошедшей через нерегулярный элемент) и бесконечного множества местных затухающих полей высших типов. С практической точки зрения основной интерес представляет влияния нерегулярного элемента на распространение по волноводу рабочей волны основного типа . В такой постановке задачи можно заменить волновод с волной эквивалентной ему длинной линией, в которой распространяются волны условных напряжений и тока (см., например [1]), а нерегулярный элемент заменить его эквивалентной схемой (схемой замещения), состоящей из сосредоточенных реактивных и активных элементов и включенной в эквивалентную длинную линию. Представление реального волноводного тракта эквивалентной схемой в виде длинной линии с включенными в эту линию схемами замещения отдельных нерегулярных элементов позволяет с помощью сравнительно простых методов теории линейных электрических цепей рассчитать прохождение волны рабочего типа по всему тракту и носит название метода эквивалентных схем. При этом, в частности, коэффициент отражения по напряженность электрического поля волны от нерегулярного элемента оказывается равным коэффициенту отражения по условному напряжению от схемы замещения этого элемента, включенной в эквивалентную длинную линию.

---

Важно понимать, что параметры эквивалентной схемы нерегулярного элемента, определяющие прохождение волны по прямоугольному волноводу, могут быть определены либо на основании решения соответствующей электродинамической задачи, либо на основании эксперимента. Таким образом, эквивалентная схема является только одним из способом представления уже готового решения волноводной задачи, полученного другим методом (теоретическим или экспериментальными).

Все исследуемые в работе нерегулярные элементы (индуктивная, емкостная и резонансная диаграммы имеют однотипную эквивалентную схему. Она изображена на рис. 4.1 и представляет собой реактивную проводимость 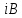, которая включена параллельно в длинную линию, эквивалентную волноводу с волной и имеющую волновую проводимость 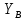. Эту проводимость можно считать равной характеристической проводимости бегущей волны .

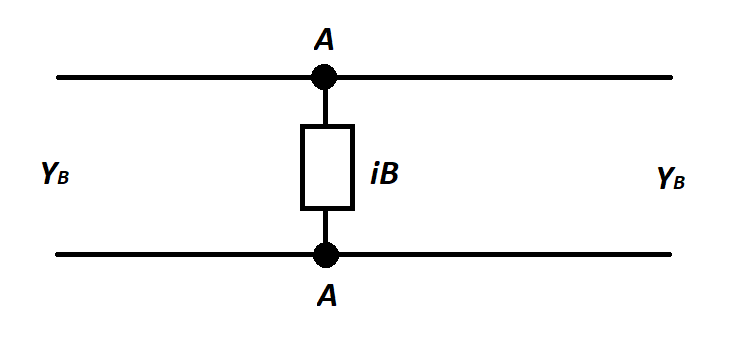Рис. 4.1. Эквивалентная схема нерегулярного элемента.

Согласно приведенной схеме в сечении 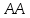, в котором расположена диафрагма, подключена параллельно линии. Результирующая проводимость 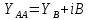, нормированное значение которой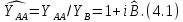



Выразив согласно теории длинных линий коэффициент отражения 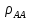через нормированную проводимость и воспользовавшись (4.1), получим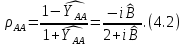



Этому коэффициенту отражения соответствует коэффициент стоячей волны



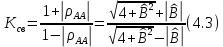
Если для конкретного вида нерегулярного элемента известна теоретическая частотная зависимость

---

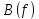, то в соответствии с (4.3) нетрудно также рассчитать теоретическую частотную характеристику КСВ этого нерегулярного элемента. С другой стороны, частотная характеристика 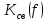нерегулярного элемента может быть получена с помощью моделирования или экспериментальным путем. Сопоставление теоретической и экспериментальной зависимостей 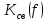показывает, насколько точны теоретические формулы для определения .

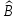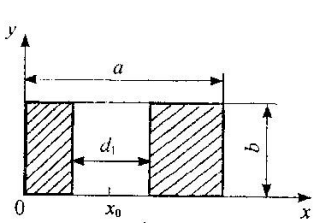
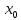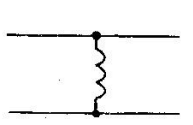
Диафрагма в волноводе представляет собой тонкую поперечную металлическую перегородку с отверстием. На рис. 4.2,а указаны геометрические параметры диафрагмы, края которой параллельны узким стенкам волновода (  – координата середины отверстия). Эквивалентная реактивность такой диафрагмы имеет для волны индуктивный характер (рис. 4.2,б), вследствие чего эту диафрагму называют индуктивной. Ее нормированная проводимость определяется приближенным выражением.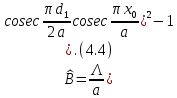



Здесь и далее  – длина волны поля в волноводе, которая выражается соотношением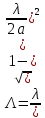



где 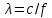 – длина волны в безграничной среде, параметры которо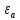й и 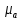совпадают с параметрами среды, заполняющей волновод (если волновод заполнен воздухом, то ).

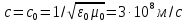а)	б)
Рис. 4.2. Индуктивная диафрагма и ее эквивалентная схема.

---

Смотрите также файлы

• По дисциплине Линейные системы автоматического регулирования комплексного тестирования в магистратуру.docx

• Но очень важная миссия быть классным руководителем. Одни учителя считают эту работу дополнительной нагрузкой к своей преподавательской деятельности, другие называют её самой главной.docx

• Сложносочиненное предложение.docx

• 1. Предмет и задачи дисциплины Основы нейрофизиологи и высшей нервнойдеятельности.docx

• Самостоятельная работа по теме Задание Составьте таблицу Странычлены нато.docx