ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное бюджетное образовательное учреждение высшего образованияСАНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТКафедра механикиРАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ №2По дисциплине: «Теоретическая и прикладная механика»Тема: «Комплексная задача по кинематике материальной точки» Вариант 12Выполнил студент гр. ЭХТ-21-2 Потапов В.А.^{(шифр группы) (подпись) (Ф.И.О.)}Проверил: профессор Мельников В.Г.^{(должность) (подпись) (Ф.И.О.)}Санкт-Петербург2023Задание. Движение точки задано координатным способом на плоскости Oxy. Следует найти траекторию точки и построить ее на рисунке. Скорость, полное ускорение и касательное ускорение найти как функцию времени. Скорость, ускорение, касательное ускорение, нормальное ускорение и радиус кривизны траектории определить в момент времени 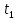. Векторы 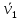, , 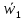, 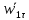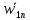показать на рисунке. 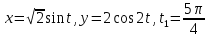cРешение:А) Определение траектории точки. Здесь следует исключить время из уравнений движения. 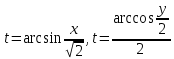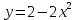В данном примере имеем:Отсюда получаем уравнение траекторииЭто гипербола. Из услови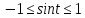й и 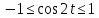следует что траекторией будет часть гиперболы, заключенная в этих интервалах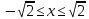

---

и 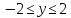. Парабола изображена на рисунке 1.

В) Определение скорости и ускорения точки в зависимости от времени. Вычисляем проекции скорости и ускорения на прямоугольные оси:

;

; ;

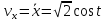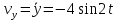
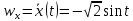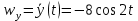Величины скорости и ускорения равны

;

;

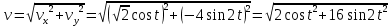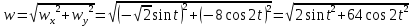Касательное ускорение будет

;

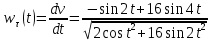С) Определение положения точки и ее кинематических характеристик в заданный момент времени. При 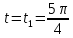с имеем координаты точки :

,

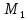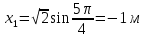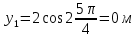
Следовательно координаты точки 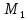равны (4, 8). По формулам предыдущего пункта находим:

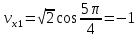м/с; , .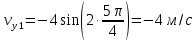

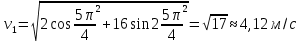Последнее означает, что вектор скорости направлен по касательной траектории вниз. Вектор полного ускорения точки строим по его проекциям:

,

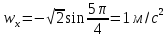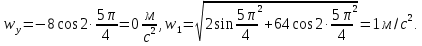
Вектор 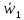направлен вправо. Далее: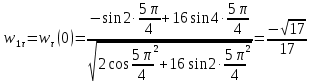

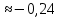м/c²

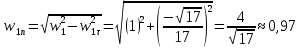м/с²

Радиус кривизны траектории будет равен

---

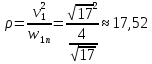
м

---

Смотрите также файлы

• Компьютерные развивающие игры.docx

• Тема Профессиональноэтические аспекты психологопедагогической диагностики.docx

• Терминология.ppt

• Искусство дизайна.odt

• 1. Общая характеристика организации места прохождения практики студентом 3.doc