Файл: Алгебра отношения сравнения целых чисел и их основные свойства. Вывод признаков делимости при помощи теории сравнений (на примере). Признаки делимости целых чисел в школьном курсе математики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| АЛГЕБРА 4. ОТНОШЕНИЯ СРАВНЕНИЯ ЦЕЛЫХ ЧИСЕЛ И ИХ ОСНОВНЫЕ СВОЙСТВА. ВЫВОД ПРИЗНАКОВ ДЕЛИМОСТИ ПРИ ПОМОЩИ ТЕОРИИ СРАВНЕНИЙ (НА ПРИМЕРЕ). ПРИЗНАКИ ДЕЛИМОСТИ ЦЕЛЫХ ЧИСЕЛ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ. 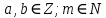  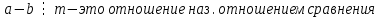 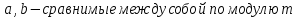 При делении на 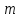 числа имеют одинаковый остаток и наз.их числа имеют одинаковый остаток и наз.ихСравнение обладает рядом свойств, но есть основные:
Если 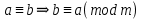 Если 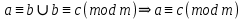 Множество всех чисел, сравнимых по данному модулю называют классом эквивалентности.
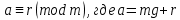
Вывод признаков делимости Возьмем число 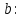 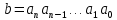 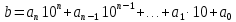 Обозначим через 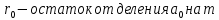 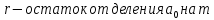 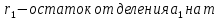 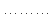 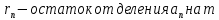 По свойствам 4 и 2: 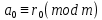 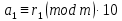 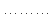 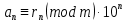 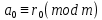 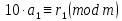 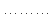 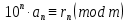 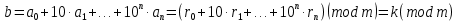 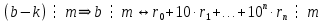 Пример: Вывести признак делимости на 11. Пусть 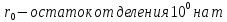 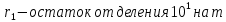 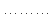 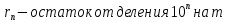 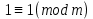 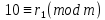 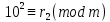 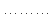 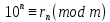 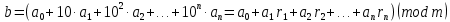 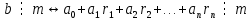 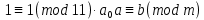 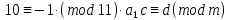 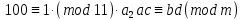 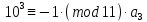 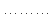 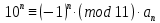 Перемножаем и складываем: 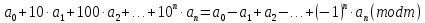  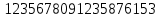 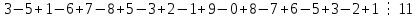 Методика: В 6 классе для упрощения вычислений изучаются признаки делимости на 2, 3, 5, 9 и 10. Эти признаки позволяют учащимся быстро определить, делится ли данное число на 2, 3, 5, 9 или 10 и выполнить деление. При этом мы должны постоянно обращать внимание на то, что деление происходит без остатка. Но этих признаков бывает недостаточно. Можно провести дополнительный урок и рассмотреть, какие числа будут делиться на 4, 6, 15, 18, 20 и 25. Признак делимости чисел на 4. На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4. Признак делимости чисел на 6 .На 6 делятся те натуральные числа, которые делятся на 2 и на 3 одновременно, то есть все четные числа, которые делятся на 3. Признак делимости на 15. Натуральное число делится на 15, если оно заканчивается на 5 или на 0 и сумма цифр делится на 3. Признак делимости на 18. Натуральное число делится на 18, если оно заканчивается на чётную цифру и сумма его цифр делится на 9. Признак делимости на 20. Натуральное число делится на 20, если число заканчивается на 0 и предпоследняя цифра четная. Для учащихся 6 класса можно предложить вывести признаки делимости на 25 и 50. Они не окажутся для них сложными. Признак делимости чисел на 25. На 25 делятся те натуральные числа, две последние цифры которых — нули или составляют число, кратное 25 (оканчиваются на 25, 50 и 75). Признак делимости чисел на 50. На 50 делятся те натуральные числа, две последние цифры которых — нули или 50. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ВАКУУМЕ И ЕГО ХАРАКТЕРИСТИКИ. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ И ОПЫТЫ ФАРАДЕЯ. ПРАВИЛО ЛЕНЦА. САМОИНДУКЦИЯ. СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. АНАЛИЗ И МЕТОДИКА И 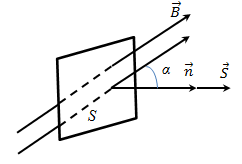 ЗУЧЕНИЯ ТЕМЫ. ЗУЧЕНИЯ ТЕМЫ.Рассмотрим однородное магнитное поле с магнитной индукцией 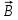 . Выделим площадь S, которую пронизывают силовые линии вектора . Выделим площадь S, которую пронизывают силовые линии вектора 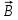 . под углом . под углом 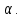 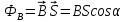 Потоком вектора магнитной индукции называется скалярная физическая величина 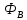 , равная скалярному произведению вектора , равная скалярному произведению вектора 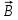 на вектор площади на вектор площади 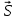 . .Поток магнитной индукции может быть положительным и отрицательным в зависимости от знака 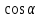 . При . При 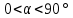 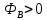 , если α – тупой , если α – тупой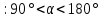 то то 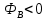 . При . При 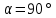 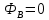 . .Магнитный поток измеряется в веберах 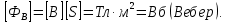 1 Вебер – это магнитный поток, создаваемый магнитным полем с индукцией в 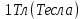 через площадь 1 м2. через площадь 1 м2.В случае неоднородного поля рассматривается элементарный поток через элементарную площадь 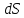 . . 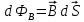 Т 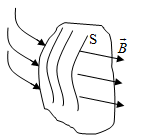 огда суммарный магнитный поток будет равен интегралу по площади огда суммарный магнитный поток будет равен интегралу по площади 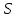 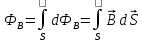
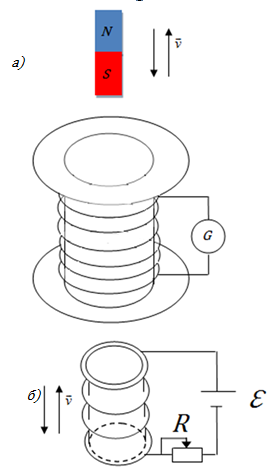
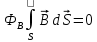 - теорема Гаусса для магнитного поля. - теорема Гаусса для магнитного поля.Опыты Фарадея а) В соленоид, замкнутый на гальванометр, вдвигается и выдвигается постоянный магнит. На гальванометре будет отклонение стрелки, и оно будет тем больше, чем быстрее происходит вдвижение и выдвижение. При изменении полюсов магнита направление отклонения стрелки изменится. б) В соленоид, замкнутый на гальванометр, вставлена катушка (другой соленоид), через которую пропускается ток. При включении и выключении (т.е. при любом изменении тока) происходит отклонение стрелки гальванометра. Направление отклонения изменяется при включении – выключении, уменьшении – увеличении тока, вдвигании – выдвигании катушек. Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает индукционный (наведенный) электрический ток. Возникновение индукционного тока означает, что в контуре действует электродвижущая сила 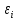 - ЭДС индукции. - ЭДС индукции.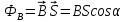 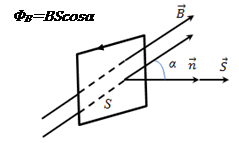 ЭДС индукции, возникающая в проводящем контуре, равна скорости изменения магнитного потока через площадь, ограниченную этим контуром – закон Фарадея. 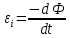 Правило Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. Знак минус в законе Фарадея является математическим выражением правила Ленца. Если контур, в котором индуцируется ЭДС, состоит не из одного витка, а из 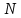 витков (например, соленоид), то если витки соединены последовательно, витков (например, соленоид), то если витки соединены последовательно,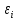 будет равна сумме ЭДС, индуцируемых в каждом из витков в отдельности: будет равна сумме ЭДС, индуцируемых в каждом из витков в отдельности: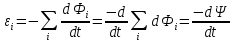 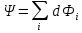 - потокосцепление или полный магнитный поток. - потокосцепление или полный магнитный поток.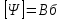 Если 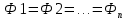 , то , то 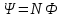 . .Т.к. 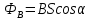 , то для того чтобы изменить магнитный поток , то для того чтобы изменить магнитный поток 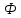 можно изменить: можно изменить:
Самоиндукция В любом случае, когда по контуру протекает электрический ток, создается магнитное поле. При этом всегда имеется магнитный поток Ф, проходящий через поверхность, ограниченную рассматриваемым контуром. Любое изменение силы тока в контуре приводит к изменению магнитного поля, сцепленного с контуром, а это в свою очередь вызывает появление индукционного тока. Это явление получило название явления самоиндукции: возникновение ЭДС индукции в проводнике при изменении в нем тока. Из закона Био-Савара-Лапласа следует 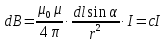 т 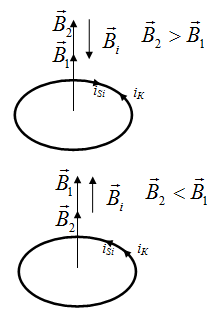 .е. магнитный поток, сцепленный с контуром, пропорционален току .е. магнитный поток, сцепленный с контуром, пропорционален току 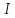 в контуре в контуре 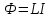 [ 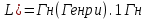 - индуктивность такого контура, магнитный поток самоиндукции к - индуктивность такого контура, магнитный поток самоиндукции к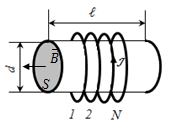 оторого при токе 1А равен 1 Вб. оторого при токе 1А равен 1 Вб. Рассчитаем индуктивность L соленоида: 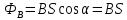 магнитная индукция 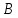 соленоида соленоида 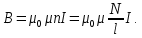 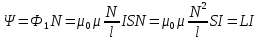 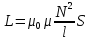 т.е. индуктивность зависит от геометрических размеров соленоида ( 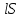 ), числа витков и магнитной проницаемости сердечника соленоида. Поэтому можно сказать, что индуктивность ), числа витков и магнитной проницаемости сердечника соленоида. Поэтому можно сказать, что индуктивность 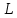 аналог емкости аналог емкости 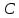 уединенного проводника, которая также зависит от геометрических размеров, от формы и диэлектрической проницаемости среды. уединенного проводника, которая также зависит от геометрических размеров, от формы и диэлектрической проницаемости среды. Применяя к явлению самоиндукции закон Фарадея, получим, что ЭДС самоиндукции 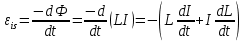 Если 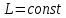 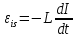 где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем возрастает, то 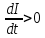 , и , и 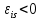 т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником и тормозит его возрастание. Если ток со временем убывает, то т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником и тормозит его возрастание. Если ток со временем убывает, то 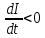 и и 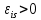 т.е. индукционный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Следовательно, контур, обладающий индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока тормозится, тем сильнее, чем больше индуктивность контура. т.е. индукционный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Следовательно, контур, обладающий индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока тормозится, тем сильнее, чем больше индуктивность контура. Система уравнений Максвелла для электромагнитного поля. В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
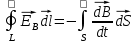 то циркуляция вектора напряженности суммарного поля: 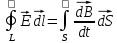 Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
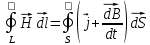 Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
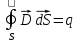 Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью 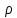 , то данная формула запишется в виде: , то данная формула запишется в виде: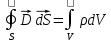
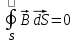 Итак, полная система уравнений Максвелла в интегральной форме: 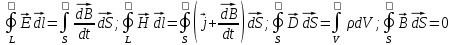  Методика 9 класс |
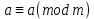
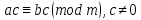
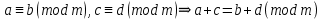
 авен нулю.
авен нулю. .
.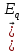 так и вихревым (
так и вихревым (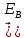 , поэтому напряженность суммарного поля
, поэтому напряженность суммарного поля 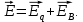 Так как циркуляция вектора равна нулю
Так как циркуляция вектора равна нулю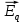 а циркуляция вектора
а циркуляция вектора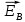 определяется выражением
определяется выражением 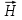 :
: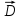 :
: