Файл: Алгебра нод и нок целых чисел. Основные свойства и алгоритм евклида. Привести примеры методов нахождения нод и нок в школьном курсе математики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| АЛГЕБРА 3. НОД И НОК ЦЕЛЫХ ЧИСЕЛ. ОСНОВНЫЕ СВОЙСТВА И АЛГОРИТМ ЕВКЛИДА. ПРИВЕСТИ ПРИМЕРЫ МЕТОДОВ НАХОЖДЕНИЯ НОД И НОК В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ Всякое целое число c, которое делит каждое из чисел 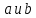 , называется их общим делителем. Целесообразно ограничиться рассмотрением натуральных делителей. Множество всех делителей является конечным, в нем присутствует наибольший, его и называют НОД. , называется их общим делителем. Целесообразно ограничиться рассмотрением натуральных делителей. Множество всех делителей является конечным, в нем присутствует наибольший, его и называют НОД.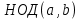 называют такой общий делитель называют такой общий делитель 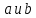 , который делится на любой их общий делитель. , который делится на любой их общий делитель.НОК. Целое число c называется наименьшим общим кратным целых чисел 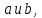 если оно делится на каждое из этих чисел. если оно делится на каждое из этих чисел.Перечислим некоторые свойства НОД и НОК. 1. Любое общее кратное чисел a и b делится на их наименьшее общее кратное. 2. Любой общий делитель чисел a и b является делителем НОД(a;b). 3. Произведение НОД и НОК чисел a и b равно произведения этих чисел. 4. Если числа a и b имеют общий делитель k, т.е. 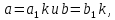 то то 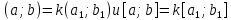 Рассмотрим один из способов нахождения НОД, а именно алгоритм Евклида: 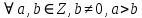 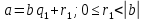 При 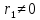 , то , то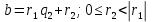 При 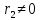 , то , то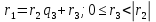 Остатки 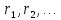 слева ограничены 0 и являются убывающими. слева ограничены 0 и являются убывающими. 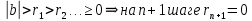 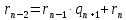 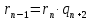 Покажем, что 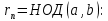
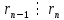 в последнем равенстве в последнем равенстве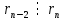 в предпоследнем в предпоследнем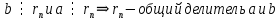 Пусть d – общий делитель 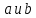 : : 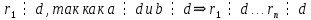 . .Найдём наибольший общий делитель чисел 140 и 96:  Последний делитель равен 4 - это значит, что НОД (140, 96) = 4. Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:
Найдём НОК (12, 16, 24) . 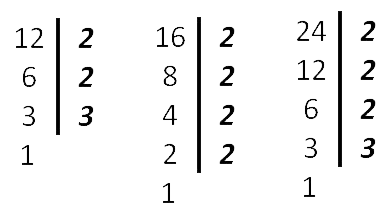 Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого большего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16 . НОК (12, 16, 24) = 2*2*2*3*2 = 48 Ответ: НОК (12, 16, 24) = 48 6.МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ. ИДЕАЛЬНЫЙ ГАЗ. ПАРАМЕТРЫ СОСТОЯНИЯ. УРАВНЕНИЕ СОСТОЯНИЯ ДЛЯ ИДЕАЛЬНОГО ГАЗА. ИЗОПРОЦЕССЫ. АНАЛИЗ И МЕТОДИКА ИЗУЧЕНИЯ ТЕМЫ. Молекулярная физика - раздел физики, в котором изучаются физические свойства тел в различных агрегатных состояниях на основе их молекулярного строения. Тепловое движение - беспорядочное (хаотическое) движение атомов или молекул вещества. Молекулярно-кинетической теорией (МКТ) называется теория, объясняющая строение и свойства тел движением и взаимодействием частиц, из которых состоят тела. В основе МКТ лежат следующие основные положения:
В молекулярно – кинетической теории используется идеализированная модель идеального газа. Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют ничтожно малые собственные размеры. У реальных газов молекулы испытывают действия силы межмолекулярного взаимодействия. Однако H2, He, O2, N2 при н. у. (Т=273К, Р=1,01 ·105 Па) можно приблизительно считать идеальным газом. Основными параметрами газа, характеризующими его состояние, являются объем, давление и температура. p, V, T. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение другого. Эта связь аналитически может быть задана в виде функции: 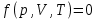 Соотношение, дающее связь между параметрами какого-либо тела, называется уравнением состояния. Следовательно, данное соотношение является уравнением состояния идеального газа. Давление (P). В газе давление возникает в результате хаотического движения молекул, в результате которого молекулы сталкиваются друг с другом и со стенками сосуда. Давление – это физическая величина, численно равная силе, действующей на единицу площади поверхности, нормальную к ней. В системе СИ давление измеряется в 1Па=1Н/м2. Температура (Т) – это мера нагретости тела. Основным уравнением, описывающим поведение идеального газа, является уравнение Менделеева-Клапейрона (уравнение состояния идеального газа): 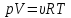 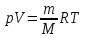 p-давление, V-объем и T-абсолютная температура газа (в градусах Кельвина), R —универсальная газовая постоянная=8,31 Дж/моль*К, общая для всех газов, а υ— число, пропорциональное числу молекул или атомов газа (так называемое число молей газа — см. Закон Авогадро). 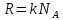 , где k=1,38*10-23Дж/К, p=nkT, n=N/V , где k=1,38*10-23Дж/К, p=nkT, n=N/V NA=6*1023 – число Авогадро k = 1,38*10-23Дж/K- постоянная Больцмана Изопроцессы - процессы изменения состояния газов так, что один из трех макроскопических параметров ( 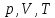 ) остается постоянным, а два других параметра при этом изменяются. ) остается постоянным, а два других параметра при этом изменяются.m=const 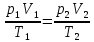
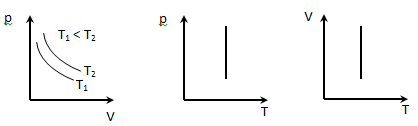 pV=const
V=V0 (1+ α t); V=V0 α T 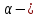 температурный коэффициент объемного расширения температурный коэффициент объемного расширения 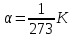 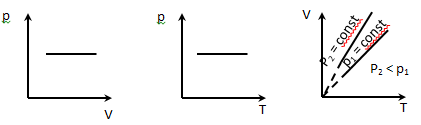
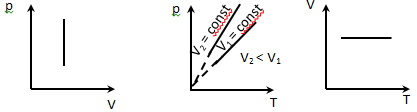 Закон Шарля: для газа данной массы при постоянном объеме 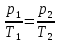 где p1, р2, T1, Т2 — давление и температура газа в начальном и конечном состояниях. Основное уравнение молекулярно-кинетической теории (м.к.т.) газов. 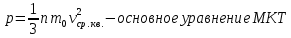 Из уравнения Менделеева - Клапейрона: 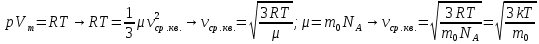 Кинетическая энергия движения частиц зависит только от температуры, при которой находится газ. 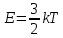 Методика изучения раздела «Основы МКТ» 10 класс Изучение этой темы основывается на знании учащихся, полученных при изучении курса в 7-8 классах и курса химии в 8-9 классах. |
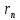 общий делитель
общий делитель