ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Угол, обозначение. Сравнение углов (п. 41)
Цели: научить давать определение угла, находить вершины угла, стороны, обозначать углы, определять углы.
Ход урока
I. Устные упражнения.
1) Какие фигуры изображены на плакате.
Как обозначается луч?Как называется точка О?
Можно ли измерить длину луча?
Почему?
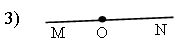Что делает точка, лежащая на прямой?Как называются лучи ОМ и ON?
II. Изучение нового материала.
План изучения:
1. Определение угла, сторон угла, вершины угла.
2. Обозначение угла.
3. Точки, лежащие внутри угла, вне угла, на сторонах угла.
4. Сравнение углов с помощью наложения.
5. Определение развернутого угла.
III. Закрепление.
1. Повторить по вопросам изучаемый материал.
2. Выполнить № 1613, 1615, 1617.
3. На повторение № 1631, 1632.
4. Запишите обозначение углов, изображенных на рисунке. Назвать стороны и вершину каждого угла.
IV. Итог урока.
V. Домашнее задание: п. 41 (до определения прямого угла); № 1638, 1639, 1643. В математический словарь: угол, стороны угла, вершина угла.
ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ
ТРЕУГОЛЬНИКА
Цели: рассмотреть теорему о точке пересечения высот треугольника.
Ход урока
I. Проверка домашнего задания.
II. Изучение нового материала.
Теорему о точке пересечения высот треугольника учителю желательно прокомментировать по заранее заготовленному чертежу, а детальное доказательство предложить учащимся провести дома самостоятельно или с помощью учебника.
III. Закрепление изученного материала.
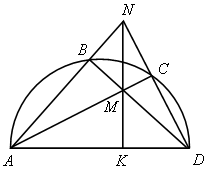 | 1. Решить устно: Дуга АD – полуокружность. Доказать MN  АD. | |
| 2. Решить №№ 677, 684, 687. № 677. Решение 1)  АВО = 180° – АВN = 180° – – СВN = CВО, то есть ВО – биссектриса АВС, аналогично СО – биссектриса АСВ.2) По теореме о биссектрисе угла точка О равноудалена от сторон АВ, ВС, АС. Таким образом, ОН1 = ОН2 = ОН3, где ОН1 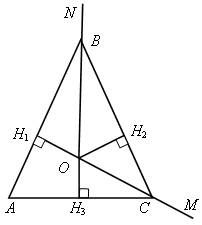АВ, ОН2 ВС, ОН3 АС. |  | |
2. Получили, что АВ, ВС, АС – касательные к окружности с центром в точке О и радиусом, равным ОН1.
№ 684.
Решение
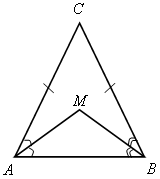 | 1) По свойству углов при основании равнобедренного треугольника  САВ = СВА.Тогда МАС = МАВ =  САВ = = СВА = МВС = МВА. |
2)
МАВ – равнобедренный, АМ = ВМ и точка М лежит на серединном перпендикуляре к АВ.3) Так как АС = СВ, то точка С также лежит на серединном перпендикуляре к АВ. Таким образом, СМ
АВ.№ 687.
Решение
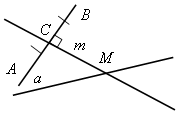 | 1) построим серединный перпендикуляр m к отрезку АВ. 2) Точка М – точка пересечения m c а. 3) М – искомая. |
Задача имеет решение в случае
, если прямая АВ не перпендикулярна к данной прямой а.
IV. итоги урока.
| 4) N – точка пересечения высот треугольника (или их продолжений). | |
Домашнее задание: вопросы 1– 20, с. 187–188; №№ 688, 720.
Рекомендовать решать № 720 методом от противного.