Файл: "Линейное программирование. Виды задач линейного программирования. Линейное программирование в банковском деле.".docx
Добавлен: 05.12.2023
Просмотров: 183
Скачиваний: 13
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, но не менее 35 млн долл., должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, т.к. в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно.
Другое дело ценные бумаги (особенно государственные). Их можно в любой момент продать, получив некоторую прибыль, или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определённой пропорции ликвидные активы – ценные бумаги, чтобы компенсировать не ликвидность кредитов. В нашем примере ограничение таково: ценные бумаги должны составлять не менее 30% средств, размещённых в кредитах и ценных бумагах.
Пусть х – средства (млн долл.), размещённые в кредитах, у – средства, вложенные в ценные бумаги. Имеем следующую систему ограничений:
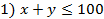– балансовое ограничение;
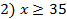– кредитное ограничение;
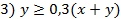– ликвидное ограничение;
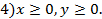
Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг:
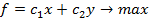
при условии 1)-4),
где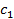
– доходность кредитов, 
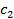– доходность ценных бумаг.
Т.к. кредиты менее ликвидны, чем ценные бумаги, то обычно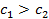
. Мы пришли к задаче линейного программирования с ограничениями 1)-4) и целевой функцией 
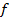, которую требуется максимизировать.
Пусть собственные средства банка в сумме с депозитными составляют 100 млн д.е.. Часть этих средств, но не менее 35 млн д.е., должна быть размещена в кредитах. Кредиты должны быть неликвидными активами банка, так как в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно. Другое дело ценные бумаги, особенно государственные. Их можно в любой момент продать, получив некоторую прибыль или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы – ценные бумаги, чтобы компенсировать не ликвидность кредитов. В нашем примере ликвидное ограничение таково: ценные бумаги должны составлять не менее 50% средств, размещенных в кредитах и ценных бумагах. Составим математическую модель задачи. Обозначим через x
1 – средства в млн д.е., размещенные в кредитах, x2 – средства, вложенные в ценные бумаги. Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг:
L=c1x1+c2x2→(max), где
c1 – доходность кредитов;
c2 – доходность ценных бумаг.
Так как кредиты менее ликвидны, чем ценные бумаги, то обычно c1>c2. Учитывая балансовое, кредитное и ликвидное ограничения, получим систему ограничений неравенств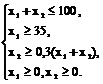
Замечание. Система ограничений, в зависимости от условий задачи, может содержать не только линейные неравенства, но и линейные уравнения.
ЗАКЛЮЧЕНИЕ
Серьезной проблемой при практическом применении линейного программирования в решении экономических задач называется большой объем информации, необходимый для передачи данных от субъектов хозяйствования к планирующему органу и обратно. Считается, что наличие денег позволяет уменьшить эти объемы, упростить передачу и обработку информации. В противоположность этому, считается, что расчет в натуральных показателях потребует не только больших вычислительных ресурсов, но и высоких требований к коммуникационным системам.
СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ
Основная литература
1. Хазанова Л.Э. Математическое моделирование в экономике. М.: Изд-во БЕК, 1998.
2. Патыка Т.Л., Попов И.И. Математические методы: Учебник, 2005.
Интернет − ресурсы
1. История линейного программирования
режим доступа :
https://stydopedia.ru/2x1fca.html
2. Виды задач линейного программирования
режим доступа :
https://function-x.ru/zadacha_lineinogo_programmirovanija.html
3.Линейное программирование
режим доступа :
https://helpiks.org/8-60929.html
Другое дело ценные бумаги (особенно государственные). Их можно в любой момент продать, получив некоторую прибыль, или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определённой пропорции ликвидные активы – ценные бумаги, чтобы компенсировать не ликвидность кредитов. В нашем примере ограничение таково: ценные бумаги должны составлять не менее 30% средств, размещённых в кредитах и ценных бумагах.
Пусть х – средства (млн долл.), размещённые в кредитах, у – средства, вложенные в ценные бумаги. Имеем следующую систему ограничений:
– балансовое ограничение; – кредитное ограничение; – ликвидное ограничение; Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг:
при условии 1)-4),
где
– доходность кредитов, – доходность ценных бумаг.Т.к. кредиты менее ликвидны, чем ценные бумаги, то обычно
. Мы пришли к задаче линейного программирования с ограничениями 1)-4) и целевой функцией , которую требуется максимизировать.Пусть собственные средства банка в сумме с депозитными составляют 100 млн д.е.. Часть этих средств, но не менее 35 млн д.е., должна быть размещена в кредитах. Кредиты должны быть неликвидными активами банка, так как в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно. Другое дело ценные бумаги, особенно государственные. Их можно в любой момент продать, получив некоторую прибыль или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы – ценные бумаги, чтобы компенсировать не ликвидность кредитов. В нашем примере ликвидное ограничение таково: ценные бумаги должны составлять не менее 50% средств, размещенных в кредитах и ценных бумагах. Составим математическую модель задачи. Обозначим через x
1 – средства в млн д.е., размещенные в кредитах, x2 – средства, вложенные в ценные бумаги. Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг:
L=c1x1+c2x2→(max), где
c1 – доходность кредитов;
c2 – доходность ценных бумаг.
Так как кредиты менее ликвидны, чем ценные бумаги, то обычно c1>c2. Учитывая балансовое, кредитное и ликвидное ограничения, получим систему ограничений неравенств
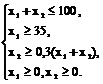
Замечание. Система ограничений, в зависимости от условий задачи, может содержать не только линейные неравенства, но и линейные уравнения.
ЗАКЛЮЧЕНИЕ
Серьезной проблемой при практическом применении линейного программирования в решении экономических задач называется большой объем информации, необходимый для передачи данных от субъектов хозяйствования к планирующему органу и обратно. Считается, что наличие денег позволяет уменьшить эти объемы, упростить передачу и обработку информации. В противоположность этому, считается, что расчет в натуральных показателях потребует не только больших вычислительных ресурсов, но и высоких требований к коммуникационным системам.
СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ
Основная литература
1. Хазанова Л.Э. Математическое моделирование в экономике. М.: Изд-во БЕК, 1998.
2. Патыка Т.Л., Попов И.И. Математические методы: Учебник, 2005.
Интернет − ресурсы
1. История линейного программирования
режим доступа :
https://stydopedia.ru/2x1fca.html
2. Виды задач линейного программирования
режим доступа :
https://function-x.ru/zadacha_lineinogo_programmirovanija.html
3.Линейное программирование
режим доступа :
https://helpiks.org/8-60929.html