Файл: Лабораторная работа 2 Исследование линейных электрических цепей постоянного тока Цель работы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 68
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Метод наложения основан на принципе независимости действия электродвижущих сил. Согласно этому принципу, токи, протекающие в цепи при наличии нескольких ЭДС, можно представить как алгебраическую сумму частичных токов, вызываемых каждой ЭДС в отдельности. Для определения частичных токов составляют на основании исходной схемы (см. рис. 2) частичные схемы, в каждой из которых действует только одна ЭДС. Все прочие ЭДС исключаются, однако, остаются в схеме их внутренние сопротивления.
Расчет частичных токов I’1, I’2, I’3 при действии ЭДС E1 по схеме рисунка 4.
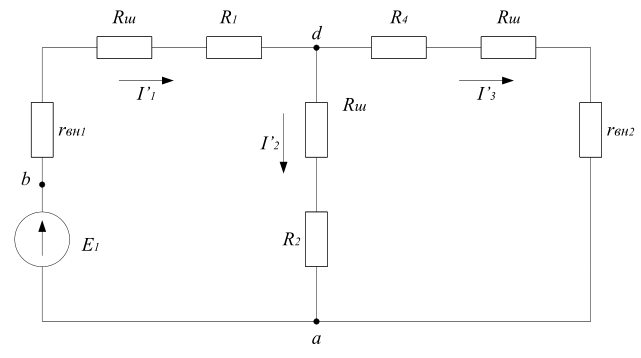
Рисунок 4
Эквивалентное сопротивление двух параллельных ветвей с резисторами R2 и R4
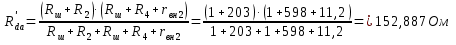
Эквивалентное сопротивление всей цепи по отношению к точкам “a” и “b”
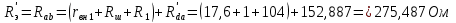
Частичный ток I’1
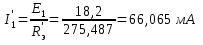
Напряжение U’da
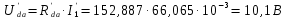
Частичные токи I’2 и I’3
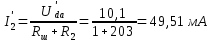
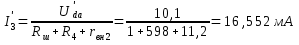
Расчет частичных токов I”1, I”2, I”3 при действии ЭДС E2 по схеме рисунка 5.
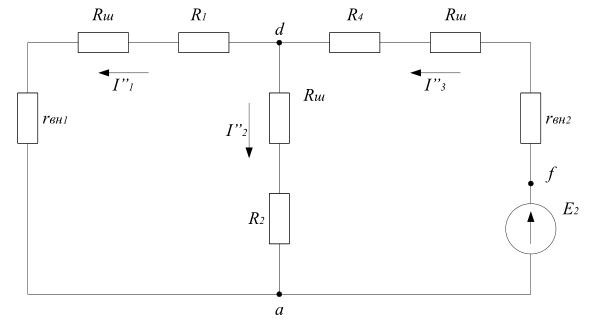
Рисунок 5
Эквивалентное сопротивление двух параллельных ветвей с резисторами R1 и R2
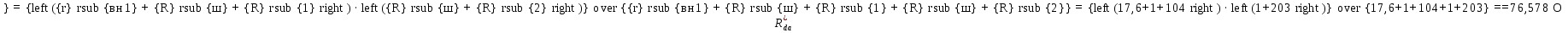
Эквивалентное сопротивление всей цепи по отношению к точкам “a” и “f”
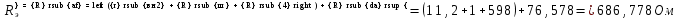
Частичный ток I”3
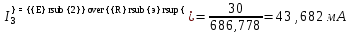
Напряжение U“da
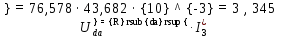
Частичные токи I”1 и I”2
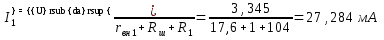
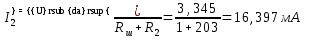
Расчет реальных токов по схеме рисунка 3.
Расчет реальных токов по схеме рисунка 3 выполняется алгебраическим суммированием (наложением) частичных токов с учетом их направления на схемах рисунков 4, 5. При этом положительным направлением реальных токов является направление, выбранное и указанное ранее на исходной схеме (см. рисунок 3). Таким образом, получаем
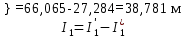
Здесь направление частичного тока I’1 совпадает с положительным направлением реального тока I1 на исходной схеме (см. рисунок 3), поэтому частичный I’1 берется со знаком «плюс». Частичный ток I”1 имеет противоположное направление (см. рисунок 5) и поэтому берется со знаком «минус». Рассуждая аналогично, находим два других реальных тока
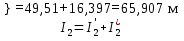
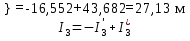
4.2.2. Рассчитать и построить отдельно потенциальные диаграммы для двух контуров a–b–c–d–e–f–a и a–b–c–d–a. Потенциал точки “d” принять равным нулю, т.е.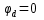
. Вычислить напряжения на участках цепи 
, 
, 
.
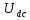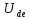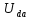Для контура a–b–c–d–e–f–a (см. рисунок 3), примем потенциал точки “d” равным нулю, т.е. φd=0 и начнем обход названного контура от точки “d” по часовой стрелке, тогда получим такой алгоритм расчета:
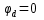
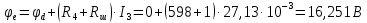
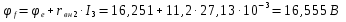
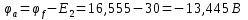
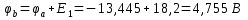
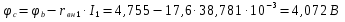
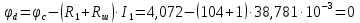
Аналогично выполняется расчет потенциальной диаграммы для любого замкнутого контура a–b–c–d–a.
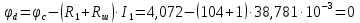
По известным потенциалам точек цепи нетрудно рассчитать напряжения между любыми из них как разность потенциалов
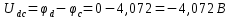
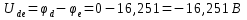
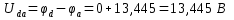
Потенциальная диаграмма для контура a–b–c–d–e–f–a представлена на рисунке 6.
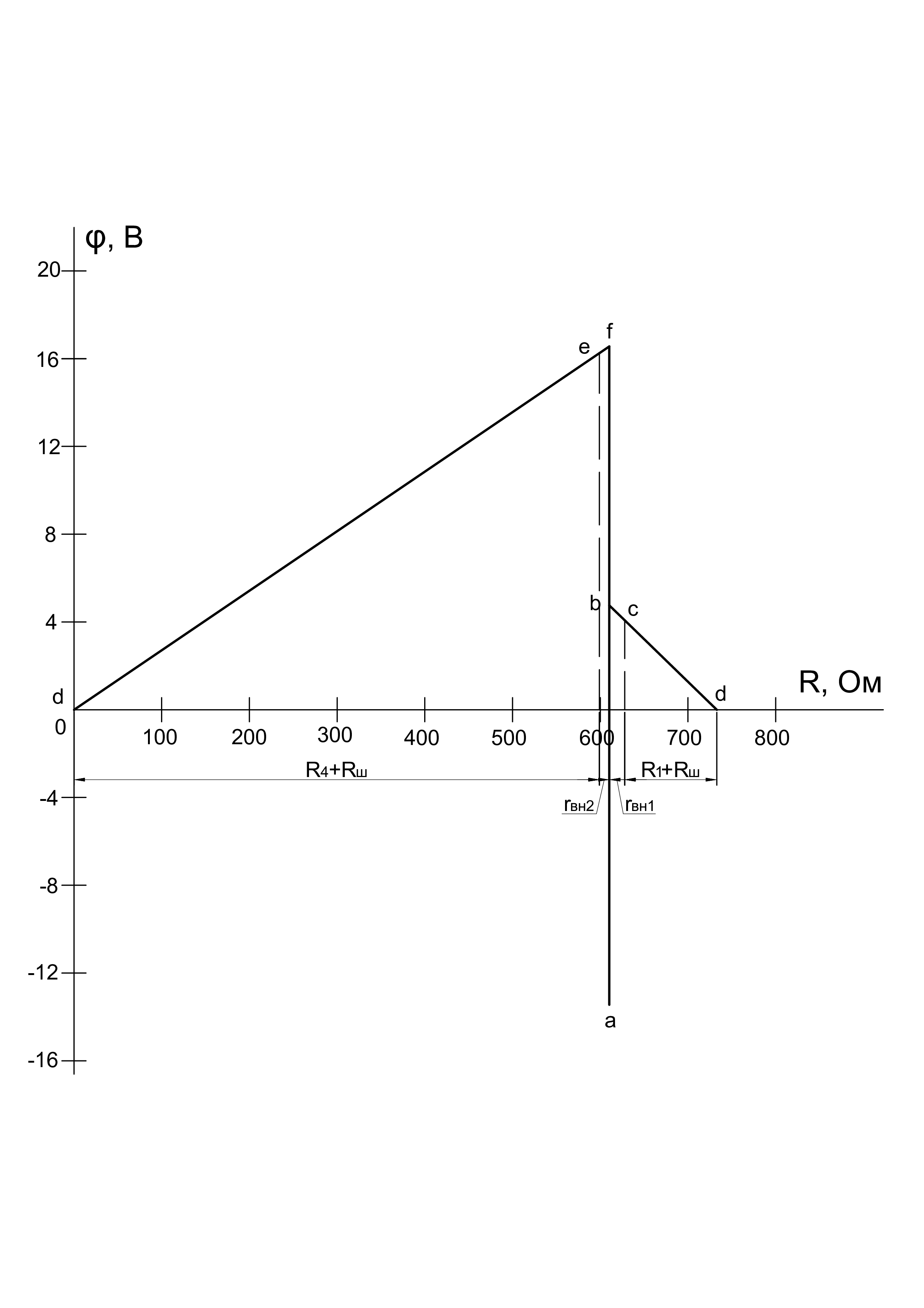
Рисунок 6
Потенциальная диаграмма для контура a–b–c–d–a представлена на рисунке 7.
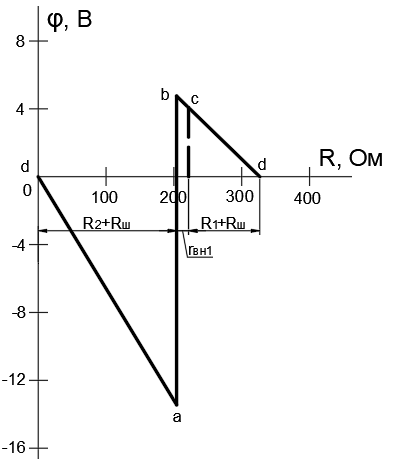
Рисунок 7
4.2.3. Результаты всех расчетов по п. 4.2. занести в таблицу 2.
5. Экспериментальная часть работы
5.1. Исследование электрической цепи с одним источником электрической энергии
5.1.1. Собрать схему, приведенную на рисунке 1.
5.1.2. Измерить токи во всех ветвях и напряжения на указанных участках цепи при пяти положениях переключателя резистора R5k, начиная с первого. Измерения выполнять в порядке, указанном в табл. 1, т.е. при одном и том же положении переключателя резистора R5k сначала измеряется ток I, I1, I2 и так далее, заканчивая исследование этого режима работы цепи измерением напряжений Uac, Uab, Ubc. Прежде, чем переходить ко второму режиму работы цепи, т.е. при втором положении переключателя, необходимо проверить правильность произведенных измерений токов и напряжений согласно законам Кирхгофа. При этом должны выполняться уравнения (см. п.4.1.4):
Такие проверки следует выполнять по окончании измерений на каждом режиме работы цепи.
5.1.3. Результаты измерений занести в табл. 1 и сравнить их с результатами, полученными при расчете в п.4.1.2. В случае значительного расхождения результатов, найти ошибки и исправить их.
Таблица 1 – Сравнение результатов расчета и эксперимента по схеме на рисунке 1.
5.1.4. По результатам эксперимента (см. табл. 1) построить на одном чертеже с теоретическими зависимостями (см. п. 4.1.5) кривые зависимостей токов ветвей I, I1, I2, I4, I5 от величины сопротивления R5к.
Подписать все кривые, проанализировать их характер и сделать выводы.
Как видно из таблицы 1, расчетные результаты и экспериментальные данные (полученные в программе симуляции электрических цепей NL5), полностью совпали, что свидетельствует о том, что расчет и эксперимент были произведены правильно. Из графика видно, что при уменьшении сопротивления R5 уменьшаются токи I5, I1 и I (значительнее всех ток I5, так как изменяется сопротивление в этой ветви. Ток I2 увеличивается, так как ветвь с этим токов включена параллельно сопротивлению R5. Ток I4 практически не изменяется.
5.2. Экспериментальное исследование электрической цепи с двумя источниками электрической энергии
5.2.1. Собрать схему, приведенную на рисунке 2, предварительно выставив регулятором на втором источнике ЭДС Е2 = 30 В.
5.2.2. После проверки правильности сборки схемы включить еѐ под напряжение и измерить токи ветвей и напряжения Udc, Ude, Uda.
5.2.3. Отключить источники ЭДС Е1 и Е2. Источник ЭДС Е2 закоротить. Включить источник ЭДС Е1. Измерить токи от действия ЭДС Е1. Результаты измерений занести в табл. 2 и сравнить их с результатами, полученными при расчете в п. 4.2.1 и 4.2.2. В случае значительного расхождения результатов, найти ошибки и исправить их.
Таблица 2 – Сравнение результатов расчета и эксперимента по схеме на рисунке 2.
Метод наложения основан на принципе независимости действия электродвижущих сил. Согласно этому принципу, токи, протекающие в цепи при наличии нескольких ЭДС, можно представить как алгебраическую сумму частичных токов, вызываемых каждой ЭДС в отдельности. Для определения частичных токов составляют на основании исходной схемы (см. рис. 2) частичные схемы, в каждой из которых действует только одна ЭДС. Все прочие ЭДС исключаются, однако, остаются в схеме их внутренние сопротивления.
Расчет частичных токов I’1, I’2, I’3 при действии ЭДС E1 по схеме рисунка 4.
Рисунок 4
Эквивалентное сопротивление двух параллельных ветвей с резисторами R2 и R4
Эквивалентное сопротивление всей цепи по отношению к точкам “a” и “b”
Частичный ток I’1
Напряжение U’da
Частичные токи I’2 и I’3
Расчет частичных токов I”1, I”2, I”3 при действии ЭДС E2 по схеме рисунка 5.
Рисунок 5
Эквивалентное сопротивление двух параллельных ветвей с резисторами R1 и R2
Эквивалентное сопротивление всей цепи по отношению к точкам “a” и “f”
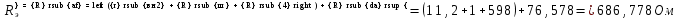
Частичный ток I”3
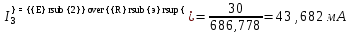
Напряжение U“da
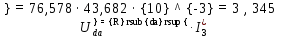
Частичные токи I”1 и I”2
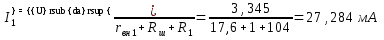
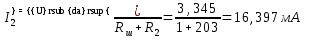
Расчет реальных токов по схеме рисунка 3.
Расчет реальных токов по схеме рисунка 3 выполняется алгебраическим суммированием (наложением) частичных токов с учетом их направления на схемах рисунков 4, 5. При этом положительным направлением реальных токов является направление, выбранное и указанное ранее на исходной схеме (см. рисунок 3). Таким образом, получаем
Здесь направление частичного тока I’1 совпадает с положительным направлением реального тока I1 на исходной схеме (см. рисунок 3), поэтому частичный I’1 берется со знаком «плюс». Частичный ток I”1 имеет противоположное направление (см. рисунок 5) и поэтому берется со знаком «минус». Рассуждая аналогично, находим два других реальных тока
4.2.2. Рассчитать и построить отдельно потенциальные диаграммы для двух контуров a–b–c–d–e–f–a и a–b–c–d–a. Потенциал точки “d” принять равным нулю, т.е.
. Вычислить напряжения на участках цепи , , .Для контура a–b–c–d–e–f–a (см. рисунок 3), примем потенциал точки “d” равным нулю, т.е. φd=0 и начнем обход названного контура от точки “d” по часовой стрелке, тогда получим такой алгоритм расчета:
Аналогично выполняется расчет потенциальной диаграммы для любого замкнутого контура a–b–c–d–a.
По известным потенциалам точек цепи нетрудно рассчитать напряжения между любыми из них как разность потенциалов
Потенциальная диаграмма для контура a–b–c–d–e–f–a представлена на рисунке 6.
Рисунок 6
Потенциальная диаграмма для контура a–b–c–d–a представлена на рисунке 7.
Рисунок 7
4.2.3. Результаты всех расчетов по п. 4.2. занести в таблицу 2.
5. Экспериментальная часть работы
5.1. Исследование электрической цепи с одним источником электрической энергии
5.1.1. Собрать схему, приведенную на рисунке 1.
5.1.2. Измерить токи во всех ветвях и напряжения на указанных участках цепи при пяти положениях переключателя резистора R5k, начиная с первого. Измерения выполнять в порядке, указанном в табл. 1, т.е. при одном и том же положении переключателя резистора R5k сначала измеряется ток I, I1, I2 и так далее, заканчивая исследование этого режима работы цепи измерением напряжений Uac, Uab, Ubc. Прежде, чем переходить ко второму режиму работы цепи, т.е. при втором положении переключателя, необходимо проверить правильность произведенных измерений токов и напряжений согласно законам Кирхгофа. При этом должны выполняться уравнения (см. п.4.1.4):
Такие проверки следует выполнять по окончании измерений на каждом режиме работы цепи.
5.1.3. Результаты измерений занести в табл. 1 и сравнить их с результатами, полученными при расчете в п.4.1.2. В случае значительного расхождения результатов, найти ошибки и исправить их.
Таблица 1 – Сравнение результатов расчета и эксперимента по схеме на рисунке 1.
| Вид исследования |  |  |  |  |  |  |  |  |  |
| мА | мА | мА | мА | мА | В | В | В | Ом | |
| Расчет | 85,824 | 58,105 | 51,483 | 27,719 | 6,622 | 16,604 | 6,101 | 10,503 |  |
| 86,764 | 59,075 | 50,899 | 27,69 | 8,176 | 16,586 | 6,203 | 10,383 |  | |
| 88,287 | 60,645 | 49,952 | 27,643 | 10,693 | 16,558 | 6,368 | 10,19 |  | |
| 91,125 | 63,571 | 48,187 | 27,554 | 15,384 | 16,505 | 6,675 | 9,83 |  | |
| 98,608 | 71,286 | 43,534 | 27,322 | 27,753 | 16,366 | 7,485 | 8,881 |  | |
| Эксперимент | 85,824 | 58,105 | 51,483 | 27,719 | 6,622 | 16,604 | 6,101 | 10,503 | |
| 86,764 | 59,075 | 50,899 | 27,69 | 8,176 | 16,586 | 6,203 | 10,383 | | |
| 88,287 | 60,645 | 49,952 | 27,643 | 10,693 | 16,558 | 6,368 | 10,19 | | |
| 91,125 | 63,571 | 48,187 | 27,554 | 15,384 | 16,505 | 6,675 | 9,83 | | |
| 98,608 | 71,286 | 43,534 | 27,322 | 27,753 | 16,366 | 7,485 | 8,881 | |
5.1.4. По результатам эксперимента (см. табл. 1) построить на одном чертеже с теоретическими зависимостями (см. п. 4.1.5) кривые зависимостей токов ветвей I, I1, I2, I4, I5 от величины сопротивления R5к.
Подписать все кривые, проанализировать их характер и сделать выводы.
Как видно из таблицы 1, расчетные результаты и экспериментальные данные (полученные в программе симуляции электрических цепей NL5), полностью совпали, что свидетельствует о том, что расчет и эксперимент были произведены правильно. Из графика видно, что при уменьшении сопротивления R5 уменьшаются токи I5, I1 и I (значительнее всех ток I5, так как изменяется сопротивление в этой ветви. Ток I2 увеличивается, так как ветвь с этим токов включена параллельно сопротивлению R5. Ток I4 практически не изменяется.
5.2. Экспериментальное исследование электрической цепи с двумя источниками электрической энергии
5.2.1. Собрать схему, приведенную на рисунке 2, предварительно выставив регулятором на втором источнике ЭДС Е2 = 30 В.
5.2.2. После проверки правильности сборки схемы включить еѐ под напряжение и измерить токи ветвей и напряжения Udc, Ude, Uda.
5.2.3. Отключить источники ЭДС Е1 и Е2. Источник ЭДС Е2 закоротить. Включить источник ЭДС Е1. Измерить токи от действия ЭДС Е1. Результаты измерений занести в табл. 2 и сравнить их с результатами, полученными при расчете в п. 4.2.1 и 4.2.2. В случае значительного расхождения результатов, найти ошибки и исправить их.
Таблица 2 – Сравнение результатов расчета и эксперимента по схеме на рисунке 2.
| Вид исследования | Действует ЭДС | | |  |  |  |  |
| мА | мА | мА | В | В | В | ||
| Расчет |  и  | 38,781 | 65,907 | 27,13 | -4,072 | -16,251 | 13,445 |
| | 66,065 | 49,51 | 16,552 | -6,937 | 9,915 | 10,1 | |
| | 27,284 | 16,397 | 43,682 | 2,865 | -26,166 | 3,345 | |
| Эксперимент | и | 38,78 | 65,91 | 27,13 | -4,072 | -16,251 | 13,446 |
| | 66,065 | 49,512 | 16,553 | -6,937 | 9,915 | 10,1 | |
| | 27,285 | 16,398 | 43,682 | 2,865 | -26,166 | 3,345 |