Задание 1.

1. Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет.

1.1.Чему равна вероятность того, что, вынимая четыре буквы, ПОЛУЧИМ слово РЕКА?

1.2.Какова вероятность сложить слово КАРЕТА при вынимании всех букв?
Решение:
Введем следующие события:
A={получили слово РЕКА}, B={получили слово КАРЕТА}.
Букв Р - 1 шт

Букв А - 2 шт

Букв К - 1 шт

Букв Е - 1 шт

Букв Т - 1 шт
Используем теорему умножения вероятности, получим:


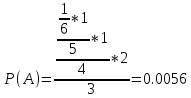
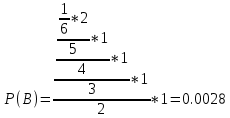
Ответ: 1) 0.0056; 2) 0.0028.

Задание 2.

Дискретная случайная величина ξ задана следующим законом распределения:

ξ	4	6	10	12
p	0,4	0,1	0,2	0,3

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение:
Найдем заданные числовые характеристики:



6.4+3.6+20+43.2=73.2- 60.84=12.36



Ответ:   7.8;   12.36;   3.516
Задание 3.

Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание 

---

 = 1.9, а также   = 7.3, найти вероятности   , которые соответствуют дискретным значениям случайной величины.
Решение:
Поскольку   , а   и   , то получим систему из трех уравнений:





Решим ее методом Гаусса:


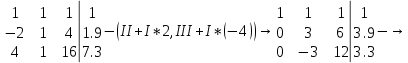
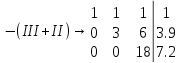
Ранг матрицы системы равен рангу расширенной матрицы, значит, система совместна. Тогда получим:
 тогда 

 тогда 

 тогда 
Ответ: 

Дискретная случайная величина ξ задана таблицей распределения
ξi -10 2 6
P(ξi) 0.25 0.45 0.3
Найдите M(ξ ) и D(ξ ).

---

Математическое ожидание = сумма произведений значений случайной ведичины на вероятности появления.

М=-10*0,25+2*0,45+6*0,3=-2,5+0,9+1,8=0,2

Дисперсия= математическое ожидание квадрата слуной величины - квадрат ее математического ожидания

D=(-10)^2*0,25+2^2*0,45+6^2*0,3 - 0,2^2=25+1,8+10,8-0,04=37,6-0,04=37,56

Задача 1. Закон распределения дискретной случайной величины X имеет вид: i x -2 -1 0 1 2 i p 0,2 0,1 0,2 4 p p5 Найти вероятности 4 p , p5 и дисперсию D(X) , если математическое ожидание M(X)  0,1

Решение: случайная величина X может принимать только пять значений, соответствующие события образуют полную группу, поэтому: p1  p2  p3  p4  p5 1 0,2  0,1 0,2  p4  p5 1 p4  p5  0,5

По определению математического ожидания: 1 1 2 2 3 3 4 4 5 5 M(X)  x p  x p  x p  x p  x p 2 4 2 5 0,1 20,2 10,1 00,  p  p p4  2p5  0,6 Вероятности 4 p и p5 найдем из решения системы: 0,5 0,5 0,1 0,4 0,1 2 0,6 0,5 4 5 5 4 5 1 5               p p p p p p p

Для нахождения дисперсии заполним вспомогательную расчетную таблицу: i x -2 -1 0 1 2 Суммы: i p 0,2 0,1 0,2 0,4 0,1 1 2 i x 4 1 0 1 4 i pi x 2 0,8 0,1 0 0,4 0,4 1,7 ( ) ( ) ( ( )) (0,1) 1,7 0,01 1,69 2 2 2 2 D X  M X  M X xi pi     Ответ: p4  0,4 , p5  0,1, D(X) 1,69

---

Смотрите также файлы

• Исследование конъюнктуры товарного рынка (на примере рынка конкретной товарной группы).docx

• Практическое задание к теме 2 Управление торговотехнологическим процессом розничной торговой организации (предприятия).docx

• Практическое задание 1 Pedagogy is a branch of science.doc

• Фармацевтический факультет Кафедра технологии лекарственных форм курсовая работа тема Вспомогательные вещества в технологии лекарственных форм аптечного изготовления по дисциплине Технология лекарственных форм аптечного изготовления.docx

• Правила подтверждения документов об образовании и о квалификации.doc