Лабораторная работа 2«Исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в однородном пласте»Цель: исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в однородном пласте.Задачи:

1. 
   изучение распределения давления, градиента давления и скорости фильтрации в залежи круговой формы при установившейся фильтрации несжимаемой жидкости по закону Дарси;
   
2. 
   определение дебита скважины, средневзвешенного по объему порового пространства пластового давления и времени движения частицы от контура питания до забоя скважины;
   
3. 
   изучение элементов гидродинамических исследований скважин на установившихся режимах фильтрации – построение индикаторных диаграмм и, на базе их обработки, определение и оценка фильтрационных свойств пласта (коэффициенты продуктивности, гидропроводности и проницаемости), при следующих исходных данных:
   

Таблица 1.Исходные данные

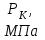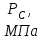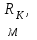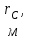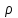				, кг/м3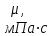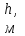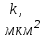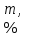
9,8	7,3	1200	0,12	995	1,5	9	0,9	19

где 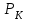– давление на контуре питания; 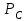– давление на забое скважины

---

;

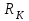– радиус контура питания;

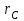– радиус скважины;

– плотность жидкости;

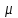– динамическая вязкость жидкости;

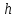– толщина пласта;

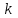– проницаемость;

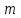– пористость.

Таблица 2.

Показатели работы скважины на различных режимах

РС1, МПа	Q1, т/сут	РС2, МПа	Q2, т/сут	РС3, МПа	Q3, т/сут	РС4, МПа	Q4, т/сут	РС5, МПа	Q5, т/сут
7,3	792	7,8	633	8,3	475	8,8	317	9,3	158

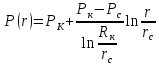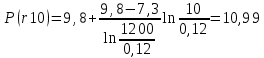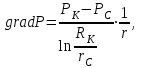
Рис. 1. Схема плоскорадиального потока Решение:1) Определение закона распределения давления в пласте: (1.1)Пример расчета: МПаРис. 2. График распределения давления по пласту в зависимости от текущего радиуса2) Определение градиента давления:Пример расчета

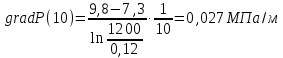
R,м	gradP,МПа/м
10	0,02714341
25	0,01085736
50	0,00542868
75	0,00361912
100	0,00271434
200	0,00135717

---

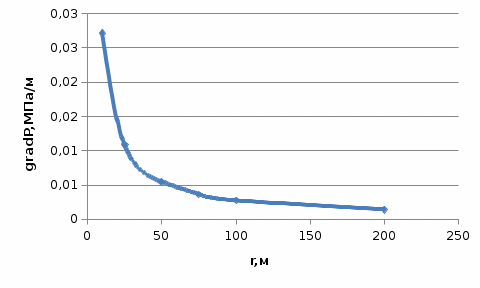
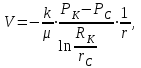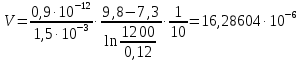Рис. 3. График распределения градиента давления по пласту в зависимости от текущего радиуса3) Определение скорости фильтрации: (1.3 м/с

	V 10-6,м/с
10	16,28604
25	6,514416
50	3,257208
75	2,171472
100	1,628604
200	0,814302

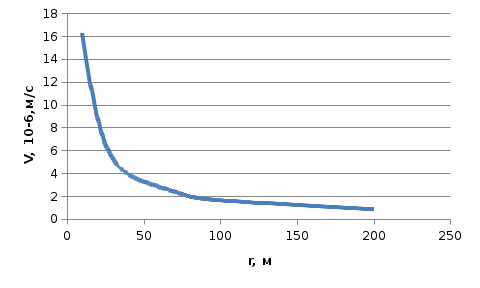
Рис. 4. График распределения скорости фильтрации по пласту в зависимости от текущего радиуса4) Определение дебита скважины (по формуле Дюпюи): 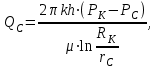(1.4)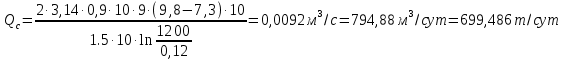5) Средневзвешенное по объему порового пространства пластовое давление: 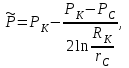(1.5) 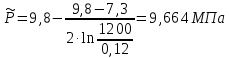6) Время движения частицы от контура питания радиуса 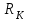до забоя скважины радиуса : 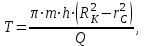(1.6)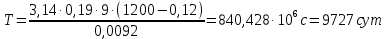Согласно варианта

Pс1, МПа	Q1, т/сут
7,3	792
7,8	633
8,3	475
8,8	317
9,3	158

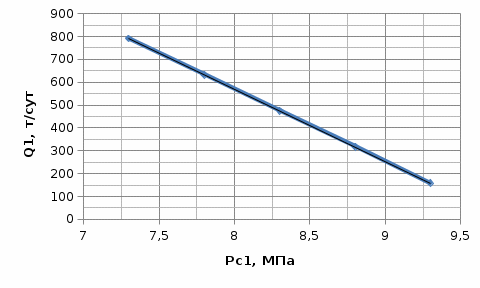
 Рис.5 Индикаторная диаграмма - зависимости 

---

«дебита  Q от забойного давления Р_с»Из данной диаграммы получаем давление на контуре питания Р_К=9,8МПа

Δpi, МПа	Q1, т/сут
7,3	792
7,8	633
8,3	475
8,	317
9,3	158
9,8	0

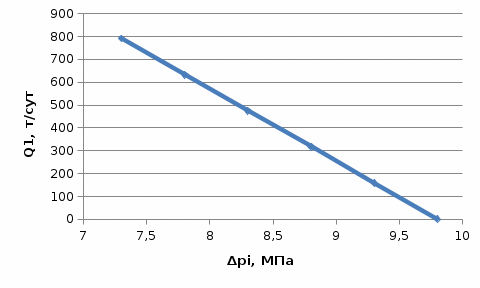
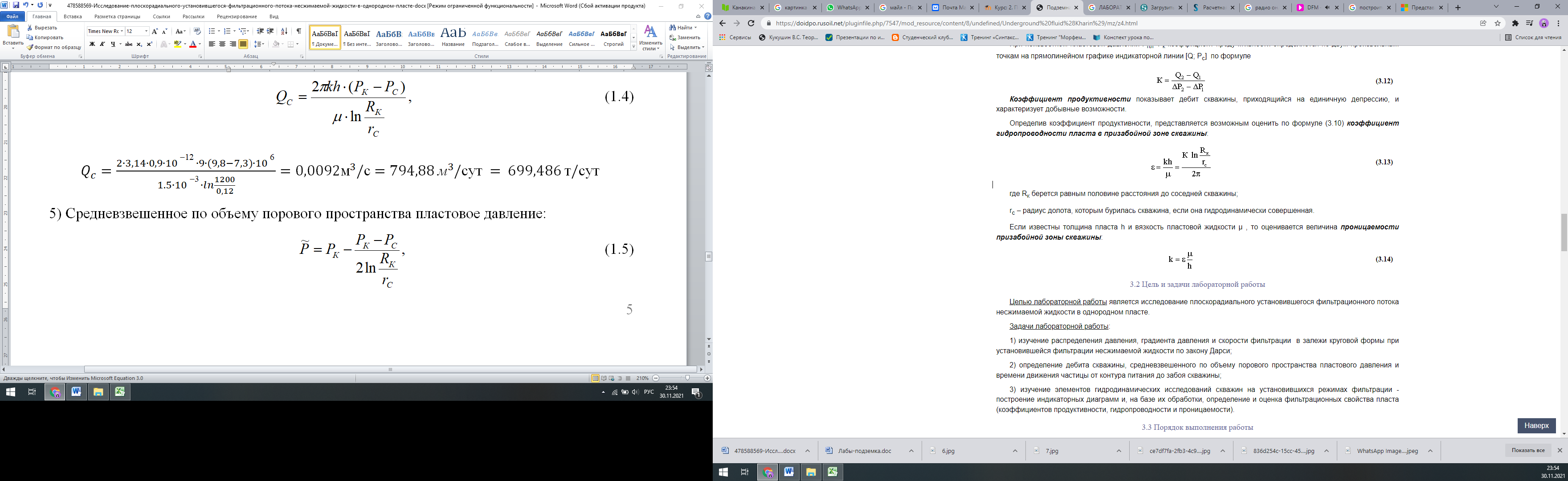
 Рис.6 Индикаторная диаграмма - зависимости «дебита  Q от забойного давления Δp»= 5,4*10^-9м³/Па*с=5,4мкм²*м/мПа*с=0,9мкм²=0,9*10^-12м²ВыводВ данной лабораторной работы были исследованы плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в однородном плате. Были расчитаны дебит скважины ( Т/сут), средневзвешенное по объему порового пространства пластовое давление (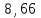 МПа) и время движения частицы от контура питания до забоя скважины ( 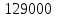сут) и построены следующие зависимости: распределения давления, градиента давления и скорости фильтрации по пласту в зависимости от текущего радиуса.В результате полученных графиков можно сказать, что давление увеличивается от скважины к контуру питания, а градиент давления и скорость фильтрации частиц уменьшаются от скважины к контуру питания.

---

Смотрите также файлы

• Для получения уравнения изоклин положим y'k. Получим Изоклинами являются гиперболы, при x0.doc

• Физиология как наука.docx

• Контрольная работа по дисциплине Огневая подготовка.docx

• Сказка о Бременских музыкантах, также созданная братьями Гримм, имеет совершенно другой тон. Это история о четырех животных осле, собаке, кошке и петухе, которые решили сбежать от своих хозяев, потому что те хотели зарезать их..docx

• Учет затрат на производство и методы калькулирования себестоимости продукцииБухгалтерский учет.pdf