Файл: Лабораторная работа 4 по дисциплине Вычислительные системы Многопоточное программирование Проверил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 50
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра вычислительной техники
ЛАБОРАТОРНАЯ РАБОТА № 4
по дисциплине «Вычислительные системы»
Многопоточное программирование
Выполнил: Проверил:
Студентки: Преподаватель: Перышкова Е.Н.
Алиева Н.И
Коломеец О.В
Группа: АММ2-22
Новосибирск
2023
Задание
1. Для программы умножения двух квадратных матриц DGEMM BLAS разработанной в лабораторной работе №3 на языке С/С++ реализовать многопоточные вычисления. В потоках необходимо реализовать инициализацию массивов случайными числами типа double и равномерно распределить вычислительную нагрузку. Обеспечить возможность задавать размерность матриц и количество потоков при запуске программы. Многопоточность реализовать несколькими способами.
1) С использованием библиотеки стандарта POSIX Threads.
2) С использованием библиотеки стандарта OpenMP.
3) *C использованием библиотеки Intel TBB.
4) **C использованием библиотеки стандарта MPI. Все матрицы помещаются в общей памяти одного вычислителя.
5) ***C использованием технологий многопоточности для графических сопроцессоров (GPU) - CUDA/OpenCL/OpenGL/OpenACC.
2. Для всех способов организации многопоточности построить график зависимости коэффициента ускорения многопоточной программы от числа потоков для заданной размерности матрицы, например, 5000, 10000 и 20000 элементов.
3. Определить оптимальное число потоков для вашего оборудования.
4. Подготовить отчет отражающий суть, этапы и результаты проделанной работы.
Ход работы
В ходе выполнения работы была написана программа на С. Многопоточность реализована с использованием библиотек стандарта POSIX Threads, OpenMP.
Были построены графики зависимости коэффициента ускорения (дефолтное время выполнения/ускоренное время выполнения) от числа потоков для заданных размерностей матрицы (128, 256, 512, 1024).
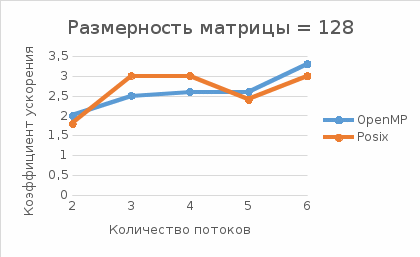
Рис.1 - Зависимость коэффициента ускорения от числа потоков для размерности матрицы = 128
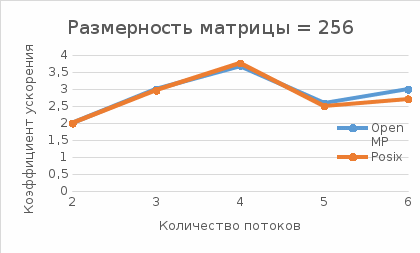
Рис.2 - Зависимость коэффициента ускорения от числа потоков для размерности матрицы = 256
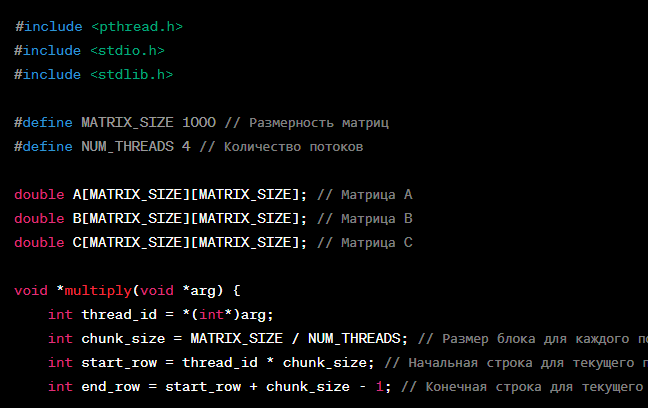
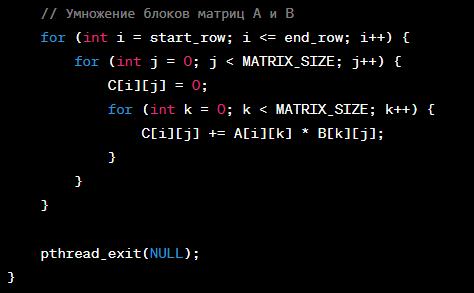
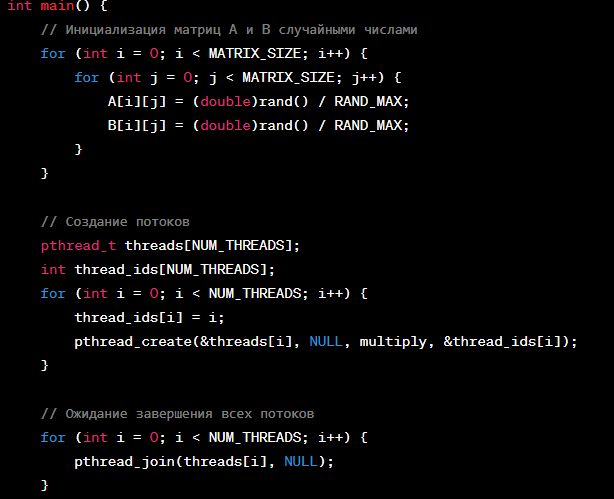
Здесь используется функция pthread_create для создания потоков, которые выполняют функцию multiply, производящую умножение блоков матриц. Каждый поток получает свой идентификатор thread_id, а также вычисляет начальную и конечную строку, для которых он отвечает.
Для синхронизации доступа к общей матрице C здесь не используется никаких мьютексов или семафоров, так как каждый поток работает с разными строками и не пересекается с другими потоками.

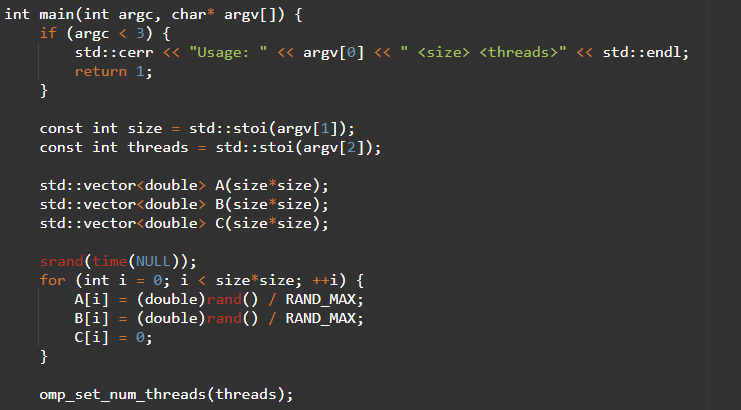
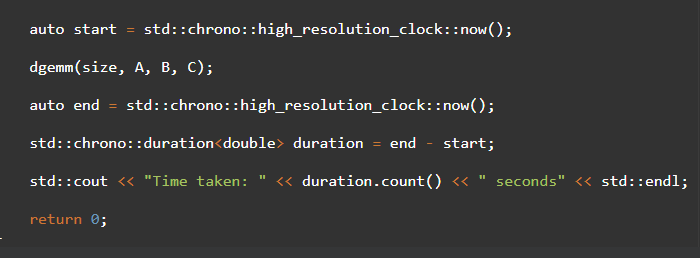
Тут мы используем директиву #pragma omp parallel for, чтобы распараллелить внешний цикл в функции dgemm(). Затем мы вызываем omp_set_num_threads() для установки количества потоков, которые мы хотим использовать.
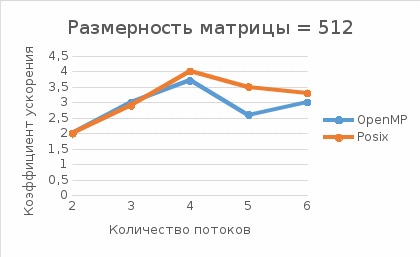
Рис.3 - Зависимость коэффициента ускорения от числа потоков для размерности матрицы = 512
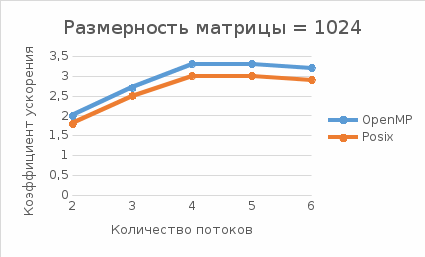
Рис.4 - Зависимость коэффициента ускорения от числа потоков для размерности матрицы = 1024
Оптимальным числом потоком для данного оборудования можно назвать 4. Оно совпадает с количеством ядер оборудования.
Вывод
В ходе выполнения лабораторной работы были изучены библиотеки для параллельных вычислений, что позволило снизить время вычислений.
Для выполнения задания использовались библиотеки OpenMP и POSIX.
В ходе работы было выявлено оптимальное число потоков (=4).
Листинг
#include
#include
#include
#define MATRIX_SIZE 1000 // Размерность матриц
#define NUM_THREADS 4 // Количество потоков
double A[MATRIX_SIZE][MATRIX_SIZE]; // Матрица A
double B[MATRIX_SIZE][MATRIX_SIZE]; // Матрица B
double C[MATRIX_SIZE][MATRIX_SIZE]; // Матрица C
void *multiply(void *arg) {
int thread_id = *(int*)arg;
int chunk_size = MATRIX_SIZE / NUM_THREADS; // Размер блока для каждого потока
int start_row = thread_id * chunk_size; // Начальная строка для текущего потока
int end_row = start_row + chunk_size - 1; // Конечная строка для текущего потока
// Умножение блоков матриц A и B
for (int i = start_row; i <= end_row; i++) {
for (int j = 0; j < MATRIX_SIZE; j++) {
C[i][j] = 0;
for (int k = 0; k < MATRIX_SIZE; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
pthread_exit(NULL);
}
int main() {
// Инициализация матриц A и B случайными числами
for (int i = 0; i < MATRIX_SIZE; i++) {
for (int j = 0; j < MATRIX_SIZE; j++) {
A[i][j] = (double)rand() / RAND_MAX;
B[i][j] = (double)rand() / RAND_MAX;
}
}
// Создание потоков
pthread_t threads[NUM_THREADS];
int thread_ids[NUM_THREADS];
for (int i = 0; i < NUM_THREADS; i++) {
thread_ids[i] = i;
pthread_create(&threads[i], NULL, multiply, &thread_ids[i]);
}
// Ожидание завершения всех потоков
for (int i = 0; i < NUM_THREADS; i++) {
pthread_join(threads[i], NULL);
}
return 0;
}
Библиотека OpenMp
#include
#include
#include
#include
void dgemm(int size, std::vector
#pragma omp parallel for
for (int i = 0; i < size; ++i) {
for (int j = 0; j < size; ++j) {
double cij = 0;
for (int k = 0; k < size; ++k) {
cij += A[i*size+k] * B[k*size+j];
}
C[i*size+j] = cij;
}
}
}
int main(int argc, char* argv[]) {
if (argc < 3) {
std::cerr << "Usage: " << argv[0] << "
return 1;
}
const int size = std::stoi(argv[1]);
const int threads = std::stoi(argv[2]);
std::vector
std::vector
std::vector
srand(time(NULL));
for (int i = 0; i < size*size; ++i) {
A[i] = (double)rand() / RAND_MAX;
B[i] = (double)rand() / RAND_MAX;
C[i] = 0;
}
omp_set_num_threads(threads);
auto start = std::chrono::high_resolution_clock::now();
dgemm(size, A, B, C);
auto end = std::chrono::high_resolution_clock::now();
std::chrono::duration
std::cout << "Time taken: " << duration.count() << " seconds" << std::endl;
return 0;
}