Практическая работа № 2 – Методы тестирования

В ходе выполнения практической работы необходимо:

• 
  разработать алгоритм решения задачи;
  
• 
  реализовать индивидуальный вариант задания на любом известном студенту языке программирования. Внести в программу несколько ошибок.
  
• 
  выполнить тестирование методами белого и черного ящика;
  
• 
  результаты тестирования представить в виде таблиц;
  
• 
  оформить отчет по лабораторной работе, включающий разделы: постановка задачи, блок-схема алгоритма решения задачи, тестовые варианты и результаты тестирования, скриншоты работы программы, код программы, выводы о достоинствах и недостатках каждой стратегии.
  

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Тестирование программного обеспечения включает в себя целый комплекс действий, аналогичных последовательности процессов разработки программного обеспечения. В него входят:

• 
  постановка задачи для теста;
  
• 
  проектирование теста;
  
• 
  написание тестов;
  
• 
  тестирование тестов;
  
• 
  выполнение тестов;
  
• 
  изучение результатов тестирования.
  

Наиболее важным является проектирование тестов. Существуют разные подходы к проектированию тестов.

Первый состоит в том, что тесты проектируются на основе внешних спецификаций программ и модулей либо спецификаций сопряжения модуля с другими модулями, программа при этом рассматривается как «черный ящик». Смысл теста заключается в том, чтобы проверить, соответствует ли программа внешним спецификациям. При этом содержание модуля не имеет

значения. Такой подход получил название — стратегия «черного ящика».

Второй подход — стратегия «белого ящика», основан на анализе логики программы. При таком подходе тестирование заключается в проверке каждого пути, каждой ветви алгоритма. При этом внешняя спецификация во внимание не принимается.

Ни один из этих подходов не является оптимальным. Реализация тестирования методом «черного ящика» сводится к проверке всех возможных комбинаций входных данных. Невозможно протестировать программу, подавая на вход бесконечное множество значений, поэтому ограничиваются определенным набором данных. При этом исходят из максимальной отдачи теста по сравнению с затратами на его создание. Она измеряется вероятностью того, что тест выявит ошибки, если они имеются в программе. Затраты измеряются временем и стоимостью подготовки, выполнения и проверки результатов теста.

---

Тестирование методом «белого ящика» также не дает 100%-ной гарантии того, что модуль не содержит ошибок. Даже если предположить, что выполнены тесты для всех ветвей алгоритма, нельзя с полной уверенностью утверждать, что программа соответствует ее спецификациям.

Например, если требовалось написать программу для вычисления кубического корня, а программа фактически вычисляет корень квадратный, то реализация будет совершенно неправильной, даже если проверить все пути.

Вторая проблема — отсутствующие пути. Если программа реализует спецификации не полностью (например, отсутствует такая специализированная функция, как проверка на отрицательное значение входных данных программы вычисления квадратного корня), никакое тестирование существующих путей не выявит такой ошибки. И наконец, проблема зависимости результатов тестирования от входных данных. Одни данные будут давать правильные результаты, а другие нет.

Таким образом, полное тестирование программы невозможно, т. е. никакое тестирование не гарантирует полное отсутствие ошибок в программе. Поэтому необходимо проектировать тесты таким образом, чтобы увеличить вероятность обнаружения ошибки в программе.
СТРАТЕГИЯ «БЕЛОГО ЯЩИКА»

Существуют следующие методы тестирования по принципу «белого ящика»:

• 
  покрытие операторов;
  
• 
  покрытие решений;
  
• 
  покрытие условий;
  
• 
  покрытие решений/условий;
  
• 
  комбинаторное покрытие условий.
  

Метод покрытия операторов

Целью этого метода тестирования является выполнение каждого оператора программы хотя бы один раз.

Тестовый пример

Исходный код программы для тестирования на языке Java	Код программы для тестирования на языке Java с ошибками
//Точка a If ((A > 1) && (B ==0)) X = X / A; //Точка c //Точка B If ((A == 2) || (X > 1)) X ++; //Точка e //Точка d	//Точка a If ((A > 1) || (B ==0)) X = X / A; //Точка c //Точка B If ((A == 2) || (X < 1)) X ++; //Точка e //Точка d

Если для тестирования задать значения переменных А = 2, В = 0, Х = 3, будет реализован путь

---

асе, т. е. каждый оператор программы выполнится один раз (рис. 1, а). Но если внести в алгоритм ошибки — заменить в первом условии and на or, а во втором Х > 1 на Х < 1 (рис. 1, б), ни одна ошибка не будет обнаружена (табл. 1). Кроме того, путь abd вообще не будет охвачен тестом, и, если в нем есть ошибка, она также не будет обнаружена. В таблице 1 ожидаемый результат определяется по блок-схеме на рис. 1 а), а фактический — по рис. 1 б). Как видно из этой таблицы, ни одна из внесенных в алгоритм ошибок не будет обнаружена.

а)	б)
Рисунок 1

Таблица 1 – результат тестирования методом покрытия операторов

Тест	Ожидаемый результат	Фактический результат	Результат тестирования
А = 2, В = 0	Х = 3	Х = 2.5	неуспешно

Метод покрытия решений (покрытия переходов)

Согласно методу покрытия решений каждое направление перехода должно быть реализовано, по крайней мере, один раз. Этот метод включает в себя критерий покрытия операторов, так как при выполнении всех направлений переходов выполнятся все операторы, находящиеся на этих направлениях.

Для программы из тестового примера покрытие решений может быть выполнено двумя тестами, покрывающими пути {ace, abd}, либо {aсd,abe}. Для этого выберем следующие исходные данные; {А = 3, В = 0, Х = 3} — в первом случае и {А = 2, В = 1, Х = 1} — во втором. Однако путь, где X не меняется, будет проверен с вероятностью 50 %: если во втором условии вместо условия Х> 1 записано Х < 1, то ошибка не будет обнаружена двумя тестами (табл. 2).

Таблица 2 – результат тестирования методом покрытия решений

Тест	Ожидаемый результат	Фактический результат	Результат тестирования
A=1, B=0	X=3	X=1	неуспешно
A=2, B=1	X=1	X=1	успешно

---

Метод покрытия условий

Этот метод может дать лучшие результаты по сравнению с предыдущими. В соответствии с методом покрытия условий записывается число тестов, достаточное для того, чтобы все возможные результаты каждого условия в решении выполнялись, по крайней мере, один раз.

В нашем тестовом примере имеем четыре условия: {А> 1, B = 0}, {А = 2, Х> 1}. Следовательно, требуется достаточное число тестов, такое, чтобы реализовать ситуации, где А > 1, А < 1, В = 0 и В <> 0 в точке а и А = 2, А <> 2, Х> 1 и Х< 1 в точке b. Тесты, удовлетворяющие критерию покрытия условий (табл. 3), и соответствующие им пути:

а) А = 2, B = 0, Х = 4 асе;

6) А = 1, В = 1, Х = 0 abd.

Таблица 3 – результаты тестирования методом покрытия условий

Тест	Ожидаемый результат	Фактический результат	Результат тестирования
A = 2, B = 0, Х = 4	X=3	X=3	неуспешно
А = 1, В = 1, Х = 0	X=0	Х=1	успешно

Критерий покрытия решений (условий)

Критерий покрытия решений/условий требует такого достаточного набора тестов, чтобы все возможные результаты каждого условия в решении выполнялись по крайней мере один раз, все результаты каждого решения выполнялись по крайней мере один раз и, кроме того, каждой точке входа передавалось управление по крайней мере один раз.

Тесты

A=2, B=0, X=4 ace;

A=1, B=1, X=0 abd.

отвечают и критерию покрытия решений/условий. Это является следствием того, что одни условия приведенных решений скрывают другие условия в этих решениях. Так, если условие А>1 будет ложным, транслятор может не проверять условия В=0, поскольку при любом результате условия В=0, результат решения ((А>1)&(В=0)) примет значение ложь. Следовательно, недостатком критерия покрытия решений/ условий является невозможность его применения для выполнения всех результатов всех условий.

Другая реализация рассматриваемого примера приведена на рисунке 2. Многоусловные решения исходной программы разбиты на отдельные решения и переходы. Наиболее полное покрытие тестами в этом случае выполняется так, чтобы выполнялись все возможные результаты каждого простого решения. Для этого нужно покрыть пути

---

HILP (тест А=2, В=0, Х=4), HIMKT (тест А=3, В=1, Х=0), HJKT (тест А=0, В=0, Х=0), HJKR (тест А=0, В=0, Х=2).

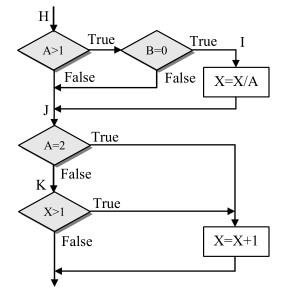Рисунок 2

Протестировав алгоритм на рисунке 2, нетрудно убедиться в том, что критерии покрытия условий и критерии покрытия решений/условий недостаточно чувствительны к ошибкам в логических выражениях.

Метод комбинаторного покрытия условий

Критерий комбинаторного покрытия условий удовлетворяет также и критериям покрытия решений, покрытия условий и по­крытия решений/условий.

Этот метод требует создания такого числа тестов, чтобы все возможные комбинации результатов условия в каждом решении выполнялись по крайней мере один раз. По этому критерию в рассматриваемом примере должны быть покрыты тестами сле­дующие восемь комбинаций:

1. 
   A > 1, B = 0. 
   
2. 
   A > 1, B <> 0. 
   
3. 
   A < 1, B = 0. 
   
4. 
   A < 1, B <> 0.
   
5. 
   А = 2, Х > 1.
   
6. 
   А = 2, Х < 1.
   
7. 
   А <> 2, Х > 1.
   
8. 
   A <> 2, X < 1.
   

Для того чтобы протестировать эти комбинации, необяза­тельно использовать все 8 тестов. Фактически они могут быть покрыты четырьмя тестами (табл. 4):

• 
  А = 2,  B = 0,  Х = 4 {покрывает 1, 5};
  
• 
  А = 2, B = 1,  Х = 1 {покрывает 2, 6};
  
• 
  А = 0.5, B = 0,  Х = 2  {покрывает 3, 7};
  
• 
  A = 1, B = 0,  Х = 1 {покрывает 4, 8}.
  

Таблица 4 – результаты тестирования методом комбинаторного покрытия условий

Тест	Ожидаемый результат	Фактический результат	Результат тестирования
A = 2, В = 0, Х = 4	Х=3	Х=3	неуспешно
A = 2, В = 1, Х = 1	Х=2	Х= 1.5	успешно
A = 0.5, B = 0, X = 2	X=3	Х=4	успешно
A = 1, В = 0, Х = 1	X=1	X=1	неуспешно

Таким образом, для программ, содержащих только одно условие на каждое решение, минимальным является критерий, набор тестов которого:

---

Смотрите также файлы

• мір, лім жне адам міріні маынасы бл.docx

• Негосударственное образовательное частное учреждение высшего образования московский финансовопромышленный университет синергия.doc

• Социальная структура общества.ppt

• Задание к Лабораторной 3.docx

• Курсовая работа по дисциплине Конституционное право.docx