Конспект урока по теме

«Решение комбинаторных задач»

МБОУ СОШ № 20 п. Железнодорожный

учитель 1 математики квалификационной

категории Суворова Л.В.

Класс: 6

Предмет: математика.

Продолжительность: 40 минут

Тип урока: объяснение нового материала

Цели:

Образовательные:

- создать представление о комбинаторике как разделе математики;

- формировать умение решать комбинаторные задачи путем перебора возможных вариантов с помощью дерева вариантов или путем перестановки закодированных элементов;

- познакомить учащихся с решением комбинаторных задач и с использованием правила умножения;

- показать применение знаний, полученных на уроках математики, на практике.

Развивающие:

- развивать логическое мышление, устную математическую речь, внимание, память и воображение через интеллектуальные задания;

- развивать умение решать комбинаторные задачи по правилу умножения;

- развивать творческий потенциал и самооценку через творческие задания.

Воспитательные:

- продолжить воспитание познавательного интереса к предмету и повышение мотивации к учению по средствам ИКТ;

- способствовать воспитанию самостоятельности и умению работать в парах.

Учебники и дидактические материалы:

- Виленкин Н.Я. и др. «Математика 6 класс» - М.: Мнемозина, 2008

- Дорофеев и др. «Математика 6 кл.» - М.: Просвещение, 1996

- Макарычев Ю.Н. и др. «Элементы статистики и теории вероятностей. Алгебра 7-9 классы» - М.: Просвещение, 2008

- Мордкович А.Г. и др. «События. Вероятности. Статистическая обработка данных. 7-9 кл.» - М.: Мнемозина, 2003

- Ткачева М.В., Федорова Н.Е. «Элементы статистики и вероятность. 7-9 кл.» - М.: Просвещение, 2006
ХОД УРОКА:

Организационный момент.

СЛАЙД 1.
СЛАЙД 2.

Сегодня на уроки мы повторим понятие стохастической линии. А как она называется вы узнаете, отгадав ребус на слайде (Комбинаторика). Мы вспомним из математики 5 класса решение комбинаторных задач путем перебора вариантов и построения дерева возможных вариантов и познакомимся с новым способом – правилом умножения.
СЛАЙД 3.

Нам часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов как это действие осуществить. Разные пути или варианты, которые приходится выбирать человеку, складываются в самые разнообразные комбинации.

---

Комбинаторика – это раздел математики, посвященный решению задач на перебор различных вариантов, удовлетворяющих каким-либо условиям. Здесь изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Латинское слово combinare означает «соединять, сочетать».

В комбинаторных задачах обычный вопрос: сколькими способами, сколько вариантов… Рождение комбинаторики как раздела математики связано с трудами великих французских математиков XVII века Блеза Паскаля и Пьера Ферма.

Существует очень много задач, в которых рассматриваются различные ситуации выбора. Однако, несмотря на все разнообразие комбинаторных задач, можно выделить среди них группы однотипных. В этих задачах речь идет о разных предметах, приводятся разные ситуации, но ход их решения одинаков, и именно поэтому такие задачи можно объединить в отдельные группы. С такими задачами мы встречались с вами в 5 классе.
СЛАЙД 4.

Например: Сколько трехзначных чисел можно составить из цифр 0, 2, 4, если цифры в записи числа не повторяются?

Составим схему рассуждений.

П ервая цифра 2 4
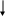
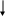
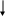
В 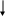торая цифра 0 4 0 2
Третья цифра 4 0 2 0
Решение: 204, 240, 402,420 – 4 числа.
Способы решения таких задач перебором возможных вариантов используются при наличии нескольких решений. При записи возможных вариантов, их схемы изображаются, как дерево с разветвленными ветвями, которое так и называется «дерево возможных вариантов».

Решим эту задачу другим способом.

На первом месте может быть только две цифры (2 или 4), на втором – две из оставшихся, а на третьем – одна. Таким образом, 2 ∙ 2 ∙ 1 = 4

---

Рассмотрим другие задачи.
СЛАЙД 5.

Задача 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 7?

	0	2	4
1	10	12	14
2	20	22	24
4	40	42	44
5	50	52	54
7	70	72	74

Решение.

Первые цифры искомых чисел: 1, 2, 4, 5, 7, так как в двузначном числе на первом месте может стоять любая цифра, кроме 0. Так как нужно составить четные двузначные числа, то второй цифрой искомых чисел могут быть: 0, 2, 4.

Составим таблицу: 5 строк (цифры 1, 2, 4, 5, 7) и 3 столбца (цифры 0, 2, 4) соответственно.

Заполняем клетки: первая цифра числа равна метке строки, а вторая цифра – метке столбца. По строкам и столбцам мы перечисляем все возможные варианты, значим, искомых чисел будет столько же, сколько клеток в таблице, то есть Ответ'>3 ∙ 5 = 15.

Ответ: из цифр 0, 1, 2, 4, 5, 7 можно составить 15 четных двузначных чисел.

Учитель: В этой задаче мы осуществили полный перебор всех возможных вариантов (комбинаций). Поэтому подобные задачи называются комбинаторными.
СЛАЙД 6.

Задача 2. На завтрак в школьной столовой любой ученик может выбрать булочку, ватрушку, кекс или сочник, а запить их он может соком, чаем или компотом. Сколько вариантов завтрака предлагается в школьной столовой?

Решение. Собираем все варианты в таблицу.

	Булочка (Б)	Ватрушка (В)	Пирожок (П)
Сок (С)	С Б	С В	С П
Чай (Ч)	Ч Б	Ч В	Ч П

В таблице 2 строки и 3 столбца, которые образуют 6 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоит один из возможных вариантов завтрака. Значит, всего вариантов столько, сколько клеток в таблице, то есть 6. Напиток можно выбрать двумя способами (сок или чай), а еду тремя способам.

---

Ответ: 2 ∙ 3 = 6 столовая предлагает 6 вариантов завтрака.
СЛАЙД 7.

З 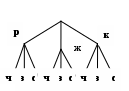адача 3. У Тани есть розовая, желтая, красная кофта и черная, зеленая, синяя юбки. Сколько различных нарядов можно составить из них?
Решение:Составим дерево возможных вариантов.

При этом возможные варианты, объекты в нем записываются

кодом. При записи объектов кодом используются буквы или

цифры. Сколько ветвей у дерева в схеме, столько решений

у задачи.

РЧ, РЗ, РС; ЖЧ, ЖЗ, ЖС; КЧ, КЗ, КС.

Кофту можно выбрать тремя способами и юбку тремя способам.

3 · 3 = 9 (нарядов)

Учитель: Что вы заметили при решении этих задач?

(Задачи разные, но решения совершенно одинаковые).

- Совершенно верно. А основаны они на общем правиле умножения
СЛАЙД 8.

Задача 4. Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой?
СЛАЙД 9.

Правило умножения:

Если объект a можно выбрать m способами, а объект b можно выбрать k

способами, то выбор пары (a, b) можно осуществить m · k способами.

СЛАЙД 10.

Примеры задач:

1. Мастер должен обшить 12 стульев обшивкой красного, коричневого и зеленого цвета. Сколькими способами он может это сделать? (12 стульев и 3 цвета, значит 12 ∙ 3 = 36)

2. Сколькими способами можно выбрать гласную и согласную буквы из слова «правило»?

(3 гласных и 4 согласных, значит 3 ∙ 4 = 12)

3. На первой полке стоит 5 книг, а на второй 10. Сколькими способами можно выбрать одну книгу с первой полки и одну со второй? (5 ∙ 10 = 50)

4. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Решение: В таких числах последняя цифра будет такая же, как и первая, а

---

предпоследняя – как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z любые цифры, а X – не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9 ∙ 10 ∙ 10 = 900 вариантов.
СЛАЙД 11.

Закрепление:

№ 53 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 720 способов; 2 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 240 способов

№ 410 10 ∙ 9 ∙ 8 ∙ 7 = 1540 номеров

№ 517 25 ∙ 24 = 600 способов

№ 915 27; 57; 87; 387; 357; 537; 837
СЛАЙД 12.

Итоги урока:

Вопросы ученикам:

• 
  Какие задачи называют комбинаторными?
  
• 
  Какие задачи называют задачами на перестановки?
  
• 
  В чем состоит правило умножения при решении комбинаторных задач?
  

Продолжите предложение по нашей теме

- Мы знаем … (как решать комбинаторные задачи по правилу умножения)

- Мы умеем … (проводить анализировать и делать выводы)

- Мы можем применить … (правило умножения при решении комбинаторных задач)

Рефлексия: А теперь оцените результаты своей деятельности на уроке.

Какое впечатление у вас об уроке? Что вам понравилось, а что нет?

Что было интересного и что еще нужно изменить? Что у вас получилось, и что нет?

Над чем еще вам нужно поработать и что повторить?
СЛАЙД 13.

Домашнее задание: № 24, № 262, № 355, № 462

Спасибо за урок.

---

Смотрите также файлы

• Медицина всегда была на переднем крае прогресса. Многие технические достижения внедрялись впервые в медицине.docx

• Играем против буллинга!.docx

• I игоровые технологии как условие создания мотивационной основы обучения иностранному языку.docx

• Меморандум конфиденциальности.doc

• Самостоятельная работа 15 по теме Сложение и вычитание рациональных чисел. I.docx