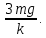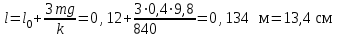Файл: Первое высшее техническое учебное заведение россии министерство науки и высшего образования российской федерации федеральное государственное бюджетное образовательное учреждение высшего образования санктпетербургский горный университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 42
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей и технической физики
Расчетно-графическое задание
По дисциплине: Физика
Вариант №8
Выполнил: студент гр. НГС-20-2 Легков А.Н.
(шифр группы) (подпись) (Ф.И.О)
Оценка:
Дата:
Проверил: Мацкевич Е.Е
(должность) (подпись) (Ф.И.О)
Санкт-Петербург
2021
Задание 1. Колеса радиуса 12 см вращается с угловым ускорением =3 рад/с .Найти для точек на ободе колеса к концу 1-ой секунды после начала движения: угловую и линейную скорости, тангенциальное, нормальное и полное ускорения, угол, составляемый вектором полного ускорения с радиусом колеса.
| Дано: R=0,12 м =3 рад/с | Решение:
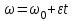 В условии сказано, что 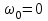 ,тогда при t=1c, ,тогда при t=1c, 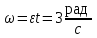
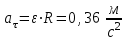
 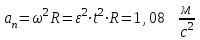
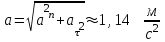
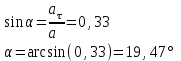 Ответ: 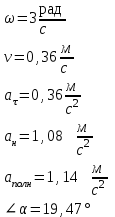 |
| Найти: 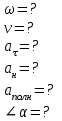 |
Задание 2. Зависимость пройденного телом пути от времени дается уравнением: S(t) = At + Bt2 +Ct3, где A, B, C – некоторые постоянные. Найти зависимость скорости и ускорения от времени; расстояние, пройденное телом, скорость и ускорение тела через время 3 с после начала движения.
| Дано: A = 4 B = 2 C = 3 t = 4 c Найти: 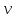 (t)-? (t)-?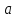 (t) - ? (t) - ?S -? 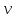 - ? - ?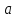 - ? - ? | Решение:
Ответ: 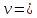 2 + 4t +9t2; 2 + 4t +9t2; 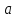 = 4 +18t; S = 240 (м); = 4 +18t; S = 240 (м); 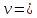 162 (м/с); 162 (м/с); 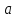 = 76 (м/с2) = 76 (м/с2) |
Задание 3. Груз массой m, привязанный к резиновому шнуру длиной l0 , отклоняют на угол 90 градусов и отпускают. Найти длину резинового шнура l в момент прохождения грузом положения равновесия. Жесткость шнура k.
| Дано: 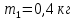 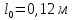 k=840 Н/м g = 9,8 м/c2 α=90 | Решение: 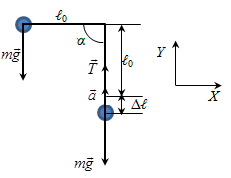
T = k Δl.
T – mg = man(1), где 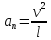 . .
Т = mg + 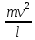 . .
Т = 3mg.
Ответ: l= 13,4 (см) |
| Найти: 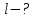 |
Задание 4. Карандаш длины l, поставленный вертикально, падает на стол. Какую угловую и линейную скорости будет иметь середина и верхний конец карандаша в момент падения?
| Дано: l = 21 см g = 9,8 м/c2 | Решение: 1 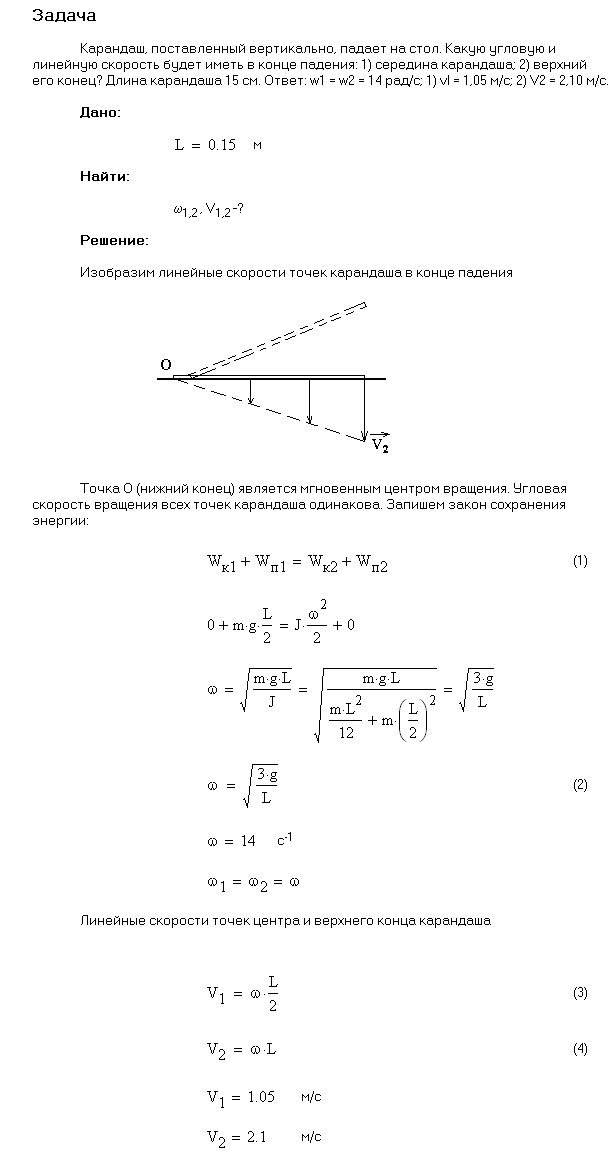 . Центр тяжести карандаша первоначально находится на высоте . Центр тяжести карандаша первоначально находится на высоте h( 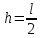 ) и имеет потенциальную энергию: ) и имеет потенциальную энергию: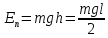 . .
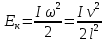
О-точка вращения 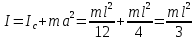 . .
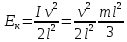 = = 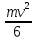
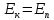 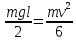 . .
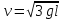 = 2,48 (м/с). = 2,48 (м/с).
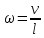 = 11,83 (рад/с). = 11,83 (рад/с).
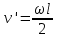 = 1,24 (м/с). = 1,24 (м/с).Ответ: 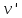 = 1,24 (м/с); = 1,24 (м/с);  = 2,48 (м/с); = 2,48 (м/с); 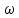 = 11,83 (рад/с) = 11,83 (рад/с) |
| Найти: 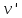 - ? - ? - ? - ?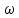 - ? - ? |
Задание 5. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузы массой m1 и m2 ( m1 > m2 ). Масса блока m, ускорение грузов a.
| Дано: 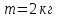 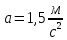 m2 = 3 кг | Решение: 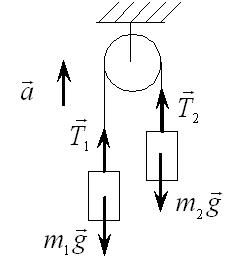 Грузы создают относительно оси блока моменты сил 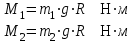 R - радиус блока, g=10 м/с² - ускорение свободного падения . По второму закону динамики для вращательного движения: 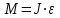 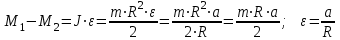 Отсюда следует: 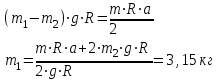 Ответ: 3,15 кг |
| Найти: 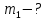 |
Задание 6. На краю платформы массы 140 кг, имеющей форму диска, вращающейся вокруг вертикальной оси с частотой1, стоит человек массой 75 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой 2с-1=0,3с-1. Момент инерции человека рассчитывается как момент инерции материальной точки.
| Дано: М =150 кг m = 75 кг 2=0,3 с-1 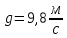 | Решение: Воспользуемся законом сохранения момента импульса: 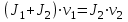 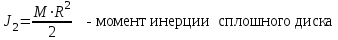 R – радиус диска, М – масса диска, 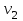 – частота вращения после перехода в центр, – частота вращения после перехода в центр, 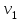 – начальная частота вращения человека с диском, – начальная частота вращения человека с диском, 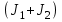 – суммарный момент инерции диска и человека, находящегося на краю диска – суммарный момент инерции диска и человека, находящегося на краю дискаМомент инерции человека, когда он стоит на краю диска: 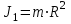 Тогда найдем частоту вращения человека и диска, когда человек стоит в центре диска 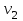 : : 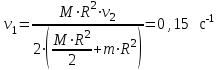 Ответ: 0,15 c-1 |
| Найти: 1 - ? |
Задание 7. Идеальная тепловая машина работает по циклу Карно. Воздух при давлении 700 и температуре 420 К занимает объем 3 л . После изотермического расширения воздух занял объем 6 л , после адиабатического расширения объем возрос до 9 л . Найти: параметры пересечения изотерм и адиабат; работу, совершаемую на каждом участке цикла; полную работу за цикл; КПД цикла; количество теплоты, полученное в цикле от нагревателя, и количество теплоты, отданное холодильнику.
| Дано: p1 =700 кПа Т1=420 К V1=3 л V2=6 л V3=9 л | Решение:
Из уравнения Бойля-Мариотта для изотермического процесса 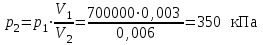
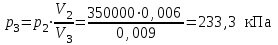
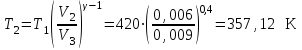
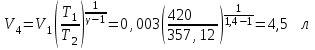
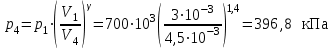
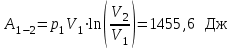
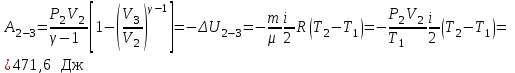
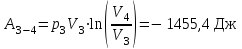
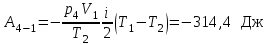
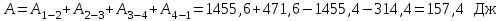
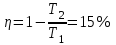
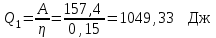
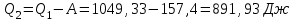 |
| Найти: А -? Аполн -? Qн -? Qх -? |
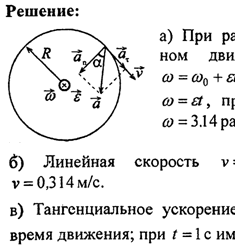 вижение в данном случае является вращательным и равнопеременным. Тогда угловая скорость:
вижение в данном случае является вращательным и равнопеременным. Тогда угловая скорость: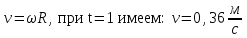
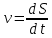 ,
, 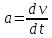 =2B +6Ct;
=2B +6Ct; 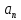 :
: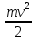 = mgl, откуда
= mgl, откуда 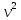 = 2gl, получаем:Т = mg +
= 2gl, получаем:Т = mg +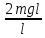 =3mg.
=3mg.