Файл: Российской федерации новосибирский государственный университет экономики и управления нинх.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 27
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЭКОНОМИКИ И УПРАВЛЕНИЯ «НИНХ»
Институт______заочного обучения__________________________
Кафедра___________ высшей математики __________________
КОНТРОЛЬНАЯ РАБОТА
Учебная дисциплина : Теория вероятностей и математическая статистика
Номер варианта контрольной работы: 1_____________________________
Наименование направления (специальности, профиля подготовки): __ _________ Экономика - Экономика предприятий и организаций
Ф.И.О студента:___ Никулина Ксения Сергеевна __________________________
Номер группы:_____________ 3ЭП51Д __________________________________
Номер зачетной книжки___________ 152471 ______________________________
Дата регистрации контрольной работы кафедрой
Проверил:_________________________________________
(Ф.И.О.)
Оценочное заключение:
Новосибирск 2016
Вариант № 1
Ситуационная (практическая) задача № 1
Между двумя населенными пунктами, отстоящими друг от друга на расстоянии 10 км, курсирует автобус с остановками по требованию в любом месте. Расстояние g (в км.), которое проезжает некий пассажир, севший в автобус в начале маршрута, является случайным с плотностью распределения
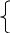 Сх(10-х), если х ε [0; 10]
Сх(10-х), если х ε [0; 10]р(х) =
0, иначе
Установить неизвестную постоянную С и построить график функции p(x)
Найти функцию распределения случайной величин ξ и построить ее график
Вычислить математическое ожидание (среднее значение), дисперсию и среднее квадратическое (стандартное) отклонение рассматриваемой случайной величины
Во сколько раз число автомашин, ожидающих заправку меньше среднего времени, превышает число автомашин, ожидающих заправку больше среднего времени?
Решение:
В силу характеристического свойства плотности распределения, имеем:
1
 =
= +
С =
Т
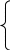 аким образом, плотность распределения имеет вид:
аким образом, плотность распределения имеет вид:Р(х) =
0, иначе
0, если х < 3
График плотности распределения изобразим на графике
Р(х)
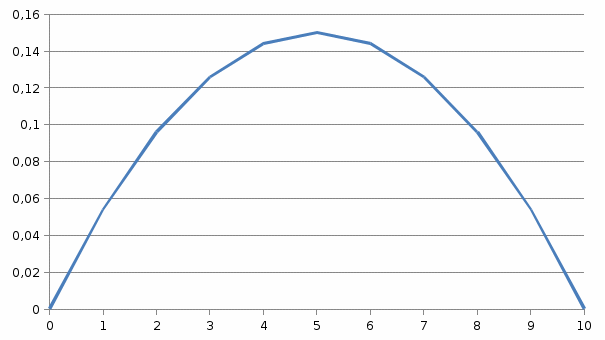
х
Функция распределения показательного закона будет иметь вид:
F
 (х) =
(х) = 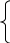 0 при х < 0
0 при х < 0F(х) = 1, если х > 10
График функции распределения
F(х)
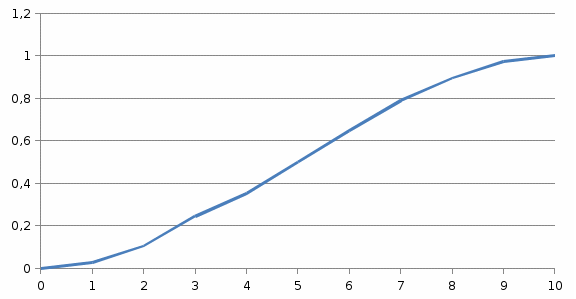
х
Вычислим:
- математическое ожидание:
Мξ =
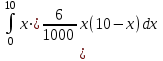
 =
= 100 = 5.
- дисперсию:
М
 (ξ2) =
(ξ2) = D ξ = 30 – 52 = 5
- среднее квадратическое отклонение:
σξ
 =
= Вычислим во сколько раз число автомашин, ожидающих заправку меньше среднего времени, превышает число автомашин, ожидающих заправку больше среднего времени.
Вероятность ожидания заправки больше среднего времени найдем, используя функцию распределения:
Вероятность получения результата меньше среднего значения:
Тогда число автомашин, ожидающих заправку меньше среднего времени, превышает число автомашин, ожидающих заправку больше среднего времени в:
0,625 : 0,375 = 1,67 раз.
Ситуационная (практическая) задача № 2
Из 10 телевизоров, среди которых 2 неисправных, наугад выбирают 3 телевизора. Составить ряд и функцию распределения числа неисправных телевизоров в выборке и представить их графически.
Решение:
Случайная величина принимает значения 0, 1, 2, 3. «Успехом испытания» принимаем выбор неисправного телевизора. По условию задачи число испытания n = 3, вероятность «успеха» р = 0,2. Следовательно, по формуле Бернулли можно вычислить вероятности:
Pk = Ck3 pk q3-k, k = 0, 1, 2, 3; q = 1 – р = 1 – 0,2 = 0,8.
P3 = C33 p3 q3-3
= 0,23 = 0,008;
P2 = C23 p2 q3-2 = 3 × 0,22 × 0,8 = 0,096;
P1 = C13 p1 q3-1 = 3 × 0,2 × 0,82 = 0,384;
P0 = C03 p0 q3-0 = 0,83 = 0,512.
Ряд и функция распределения имеют вид
| хk | 0 | 1 | 2 | 3 |
| pk | 0,512 | 0,384 | 0,096 | 0,008 |
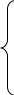
0, если х ≤ 0;
0,512, если 0 < х ≤ 1;
F (x) = 0,896, если 1 < х ≤ 2;
0,992, если 2 < х ≤ 3;
1, если х > 3.
На рис. 2.1 и 2.2 представлены многоугольник и график функции распределения.
pk
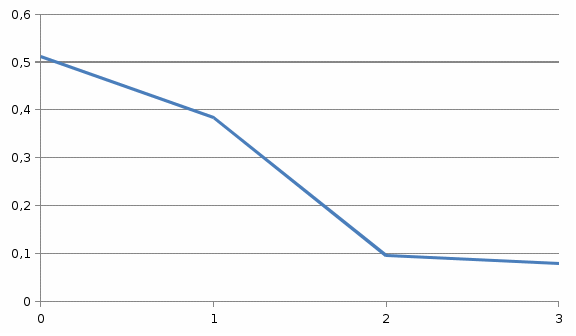
хk
Рис. 2.1. Многоугольник распределения
F
 (x
(x
)1
0
 ,992
,9920
 ,896
,8960
 ,512
,512
1 2 3 х
Рис. 2.2. Функция распределения
Тестовые задания
Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.
1. В коробке смешаны электролампы одинакового размера и формы: по 150 Вт – 6 штук и по 100 Вт – 12. Вынуты из коробки наугад три лампы. Найти вероятность того, что среди них две лампы по 150 Вт
А. 0,221
Б. 0,225
В. 0,018
Г. 0,125.
2. Рабочий обслуживает три станка. В течение смены первый станок работает бесперебойно в среднем 90% всего времени, второй – 80%, третий – 85%. Найти вероятность того, что среди этих станков в течение смены хотя бы один будет работать бесперебойно.
А. 0,997
Б. 0,612
В. 0,003
Г. 0,388.
3. По самолету производится три независимых выстрела. Вероятность попадания при первом выстреле равна 0,2, при втором - 0,4, при третьем – 0,7. Для вывода самолета из строя достаточно трех попаданий. При двух попаданиях он выходит из строя с вероятностью 0,7, при одном попадании – с вероятностью 0,4. Найти вероятность того, что в результате трех выстрелов самолет будет выведен из строя.
А. 0,332
Б. 0,468
В. 0,056
Г. 0,476.
4. В группе из 25 студентов, пришедших сдавать экзамен, имеется 2 подготовленных отлично, 6 – хорошо, 12 – удовлетворительно, а остальные студенты подготовлены плохо. Отлично подготовленные студенты знают все 35 вопросов программы, подготовленные хорошо – 28, подготовленные удовлетворительно – 19 и подготовленные плохо знают лишь 8 вопросов программы из 35. На экзамене наугад вызванный студент ответил на один вопрос из трех заданных. Как вероятнее всего он подготовлен?
А. отлично
Б. плохо
В. удовлетворительно
Г. хорошо.
5. Согласно статистическим данным в городе N в среднем 15% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из 5 наугад выбранных новых предприятий к концу года деятельности останется ровно 3?
А. 0,976
Б. 0,138
В. 0,0024
Г. 0,024.
6. Из-за болезни на работу ежедневно не выходит в среднем 5% работников предприятия. Какова вероятность того, что из 5 работников, выбранных наудачу из списочного состава предприятия, на работе будет присутствовать не менее 3 сотрудников предприятия?
А. 0,0012
Б. 0,0226
В. 0,9774
Г. 0,9989.
7. По результатам проверок налоговыми инспекциями установлено, что в городе N в среднем 20% малых предприятий нарушают финансовую дисциплину. Какова вероятность того, что из ста малых предприятий города N нарушения финансовой дисциплины будут иметь не менее 15, но не более 30 малых предприятий?
А. 0,3944
Б. 0,8882
В. 0,4938
Г. 0,0994.
8. В результате проверки качества приготовленных для посева семян огурца установлено, что в среднем 85% семян всхожи. Сколько нужно посеять семян, чтобы с вероятностью 0,94 можно было утверждать, что доля взошедших семян среди них отклонится по абсолютной величине от вероятности взойти каждому семени не более, чем на 0,01?
А. 68
Б. 4507
В. 100
Г. 94.
9. Два бухгалтера независимо друг от друга заполняют одинаковые ведомости. Первый бухгалтер допускает ошибки в среднем в 5%, второй – в 10% всех документов. Количество заполненных ведомостей первым бухгалтером равно 2, вторым – 1. Найти математическое ожидание и дисперсию числа ведомостей, заполненных бухгалтерами без ошибок.