Добавлен: 06.12.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство цифрового развития, связи и массовых коммуникаций
Российской Федерации
Уральский технический институт связи и информатики (филиал) ФГБОУ ВО "Сибирский государственный университет телекоммуникаций и информатики" в г. Екатеринбурге (УрТИСИ СибГУТИ)
КАФЕДРА
ИТиМС
ОТЧЕТ
По дисциплине «Теория связи»
Лабораторная работа № 1
«Дискретизация и восстановление
Непрерывных сигналов»
| Выполнил: | студент гр. ТЕ-11б Морозов В.О. |
| Проверил: | преподаватель Потапов Н.С. |
Екатеринбург, 2023
1. Цель работы:
Изучение процессов временной дискретизации аналоговых сигналов и их последующего восстановления с помощью фильтра нижних частот (ФНЧ).
Задание :
1.1. Перед запуском компьютерной модели следует установить два временных параметра процесса моделирования. Для этого в команде главного меню Simulation (Моделирование) выбрать подкоманду Configuration Parameters (Параметры моделирования) и задать параметру Stop time (Конечное время) значение 0.002, а параметру Max step size (Максимальный шаг интегрирования) – значение 1e-6/10.24.
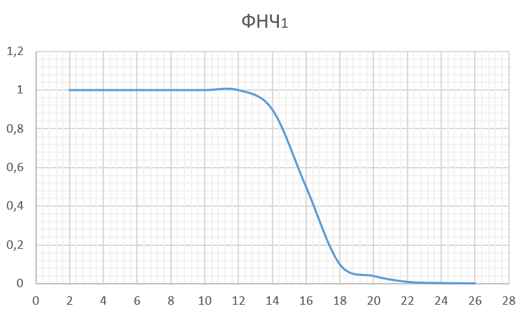
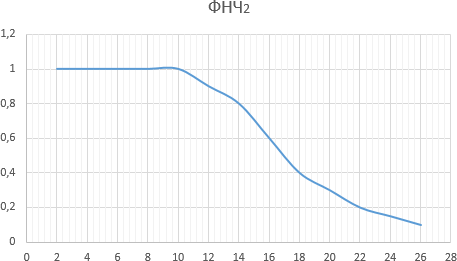
1.2. Снять АЧХ фильтров ФНЧ1 и ФНЧ2. Для этого дважды щёлкнуть мышкой по переключателю Switch2 и с выхода блока Sine Wave подать на входы фильтров гармонический сигнал амплитудой 1 В с частотой, меняющейся в пределах от 2 до 26 кГц с дискретом 2 кГц. Амплитуду выходного сигнала измерять с помощью осциллографов OutContSignal1 и OutContSignal2.
2 кГц

4 кГц

6 кГц

8 кГц

10 кГц

12 кГц

14 кГц

16 кГц

18 кГц

20 кГц

22 кГц

24 кГц

26 кГц

Построить графики АЧХ для каждого из фильтров, определить их частоты среза и оценить степень близости их АЧХ к АЧХ идеального ФНЧ.
1.3. Исследовать импульсные реакции ФНЧ1 и ФНЧ2, подав на входы ФНЧ последовательность коротких импульсов. Для этого сначала установить оба переключателя в нижнее положение, задать для генератора Pulse Generator период (параметр Period), равный 0.8е-3 с, а частоту дискретизации в блоке Discretizator равной 2е3, т.е. 2 кГц.
Зафиксировать графики импульсных реакций с экрана осциллографа в протоколе исследований, построить их в одинаковом масштабе, измерить задержку каждого из сигналов относительно момента подачи импульсов, оценить форму каждого из сигналов с точки зрении ее близости к форме импульсной реакции идеального ФНЧ.
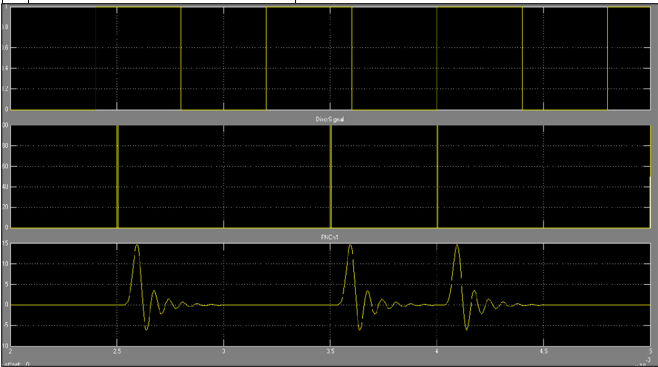
Импульсная реакция ФНЧ 1
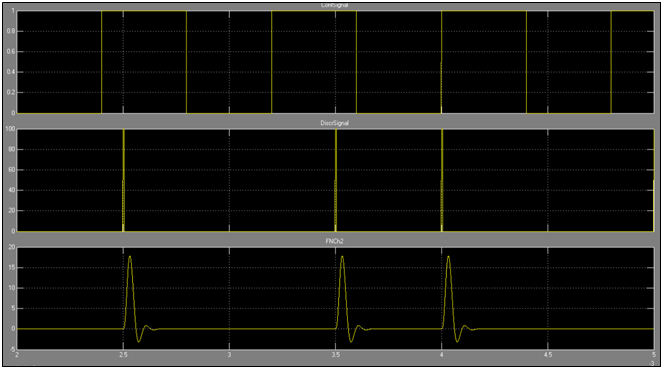
Импульсная реакция ФНЧ 2
На ФНЧ 2 задержка сигнала равна 0.1 мс
1.4. Исследовать процесс дискретизации и восстановления видеоимпульсов длительностью 0.8 мс (параметр Period блока Pulse Generator) на частотах дискретизации 10, 20, 40 и 80 кГц (параметр Frequency digitations блока Discretizator).
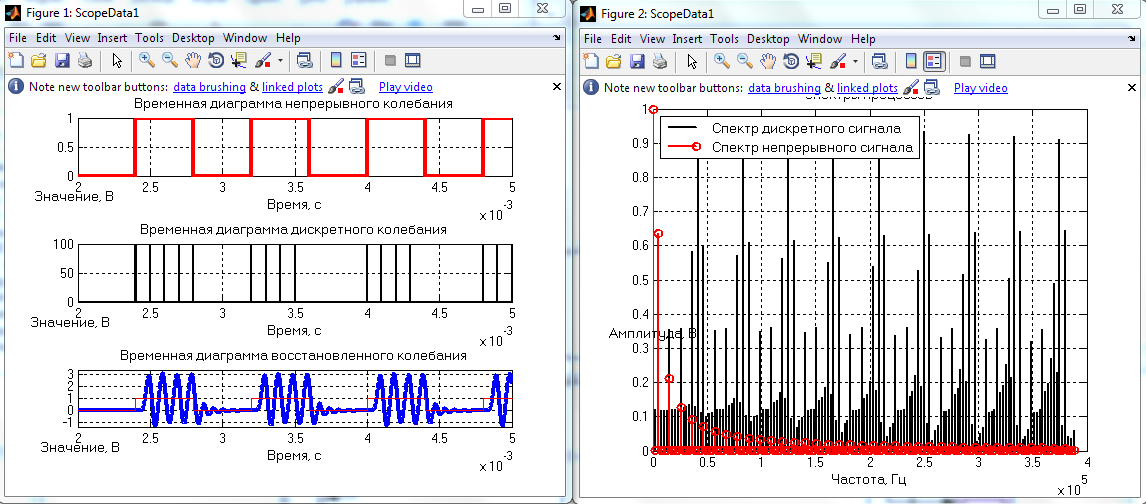
10 кГц Первый фильтр
10 кГц Второй фильтр
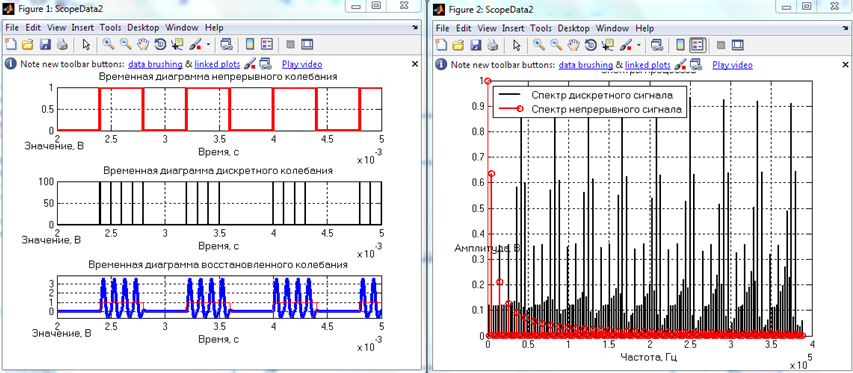
Измерения с 20кГц
 20 кГц Первый фильтр
20 кГц Первый фильтр20 кГц Второй фильтр
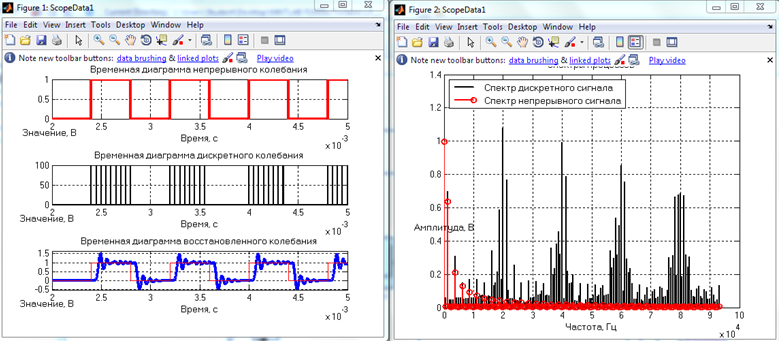
Измерения с 40 кГц
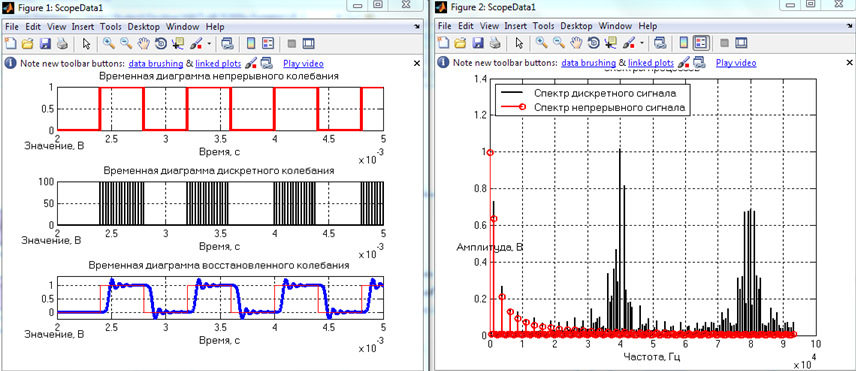
40 кГц Первый фильтр
40 кГц Второй фильтр
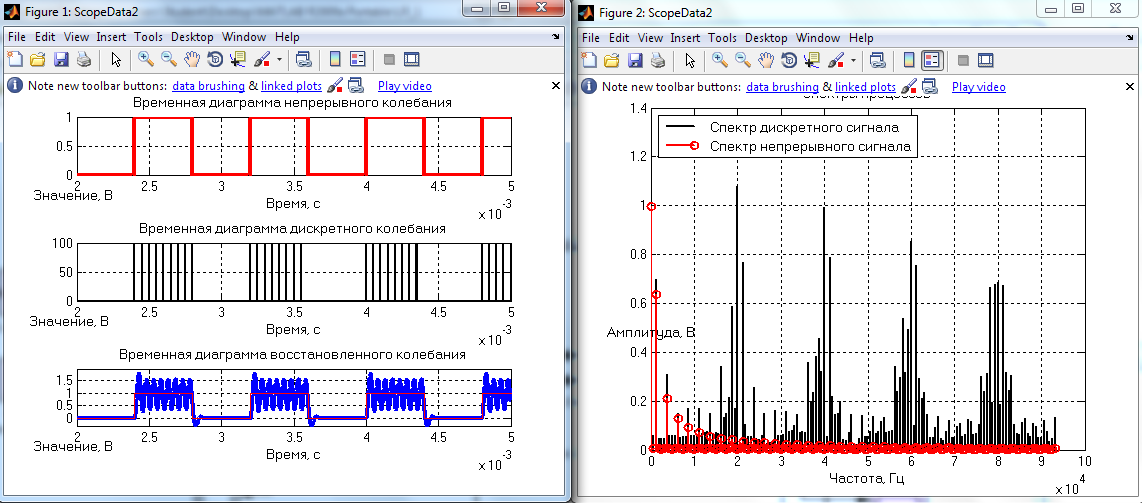
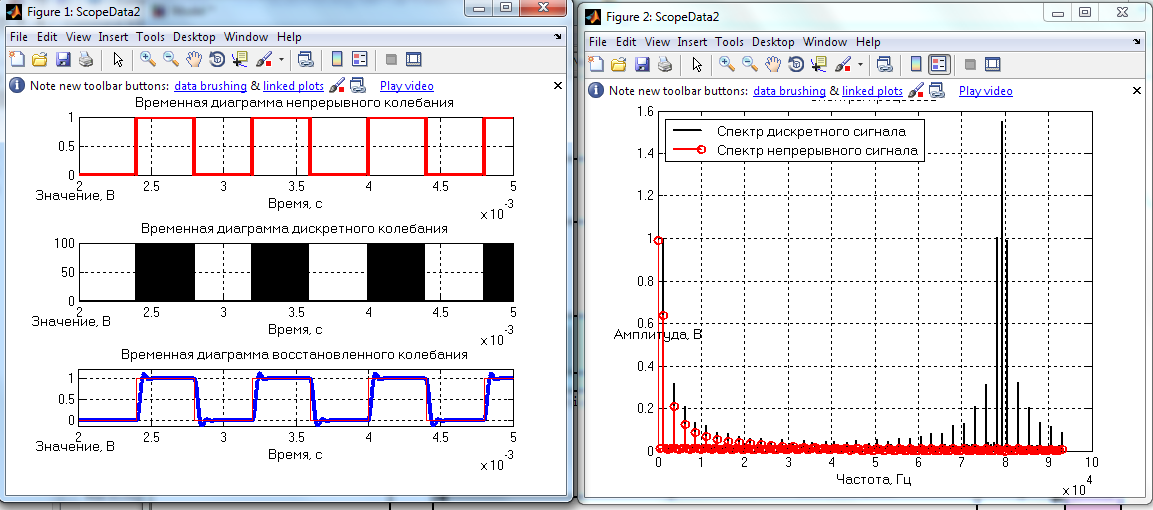
Измерения с 80 кГц
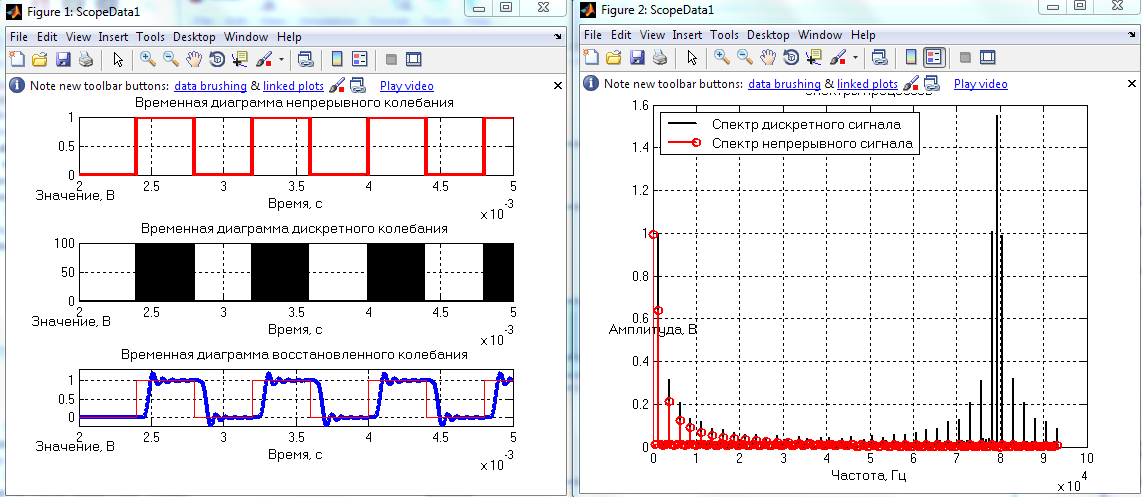
80 кГц Первый фильтр

80 кГц Второй фильтр
1.5.1 Исследовать процесс дискретизации и восстановления радиоимпульсов длительностью 0,8 мс с несущей частотой, равной 10 кГц (параметр Frequency Period блока Sine Wave).
исходный, дискретизированный и восстановленный сигналы при фазе 0, (ФНЧ1; ФНЧ2).
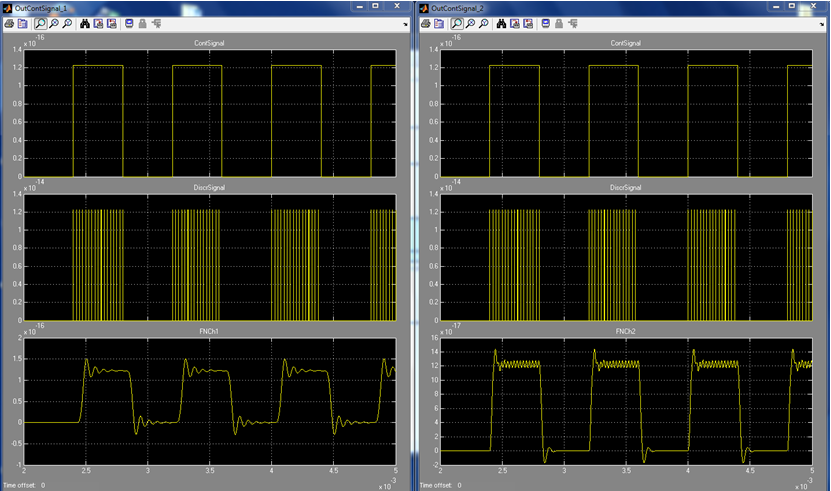
исходный, дискретизированный и восстановленный сигналы при фазе 90 гр., (ФНЧ1; ФНЧ2).
исходный, дискретизированный и восстановленный сигналы при фазе π, (ФНЧ1; ФНЧ2).
1.5.2 Исследовать процесс дискретизации и восстановления сформированного в п. 1.5.1. непрерывного сигнала при частоте дискретизации 20 кГц (параметр Frequency Period блока Sine Wave). Наблюдать изменение формы дискретизированного сигнала от сдвига фазы несущей.
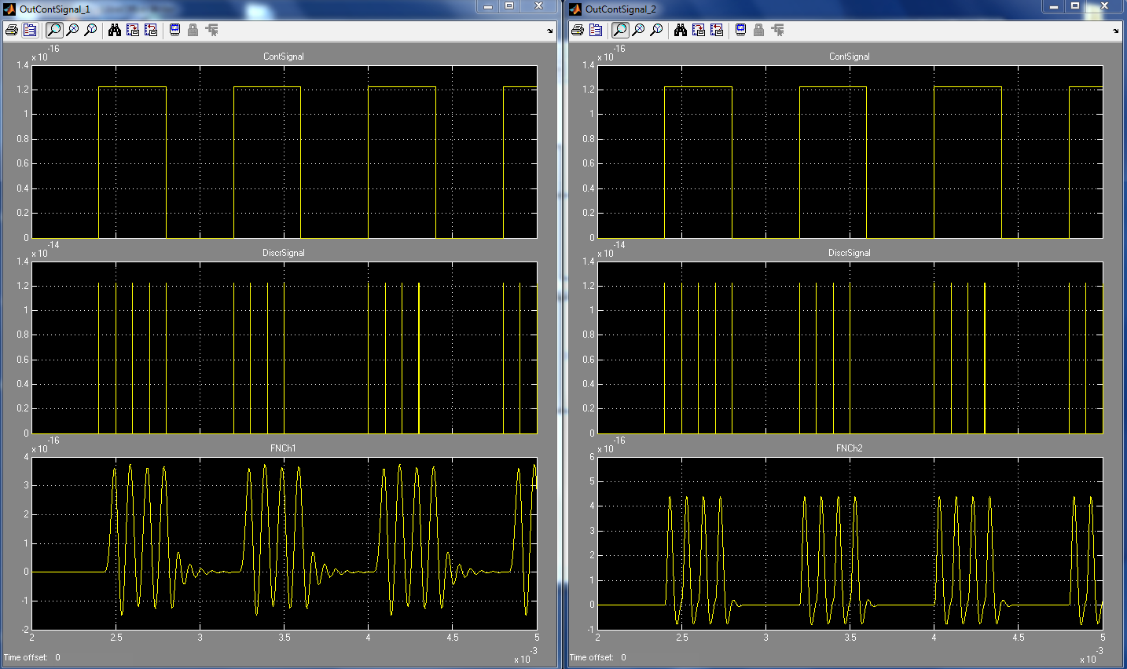
График исследования процесса дискретизации восстановления
радиоимпульсов fд = 20 кГц
1.5.3. Сформировать на выходе генератора импульс длительностью 0,8 мс (параметр Period блока Pulse Generator), установить фазу гармонического колебания равной 0 (параметр Phase блока Sine Wave), перевести переключатель Switch1 в верхнее положение. Установить частоту дискретизации 40 кГц.
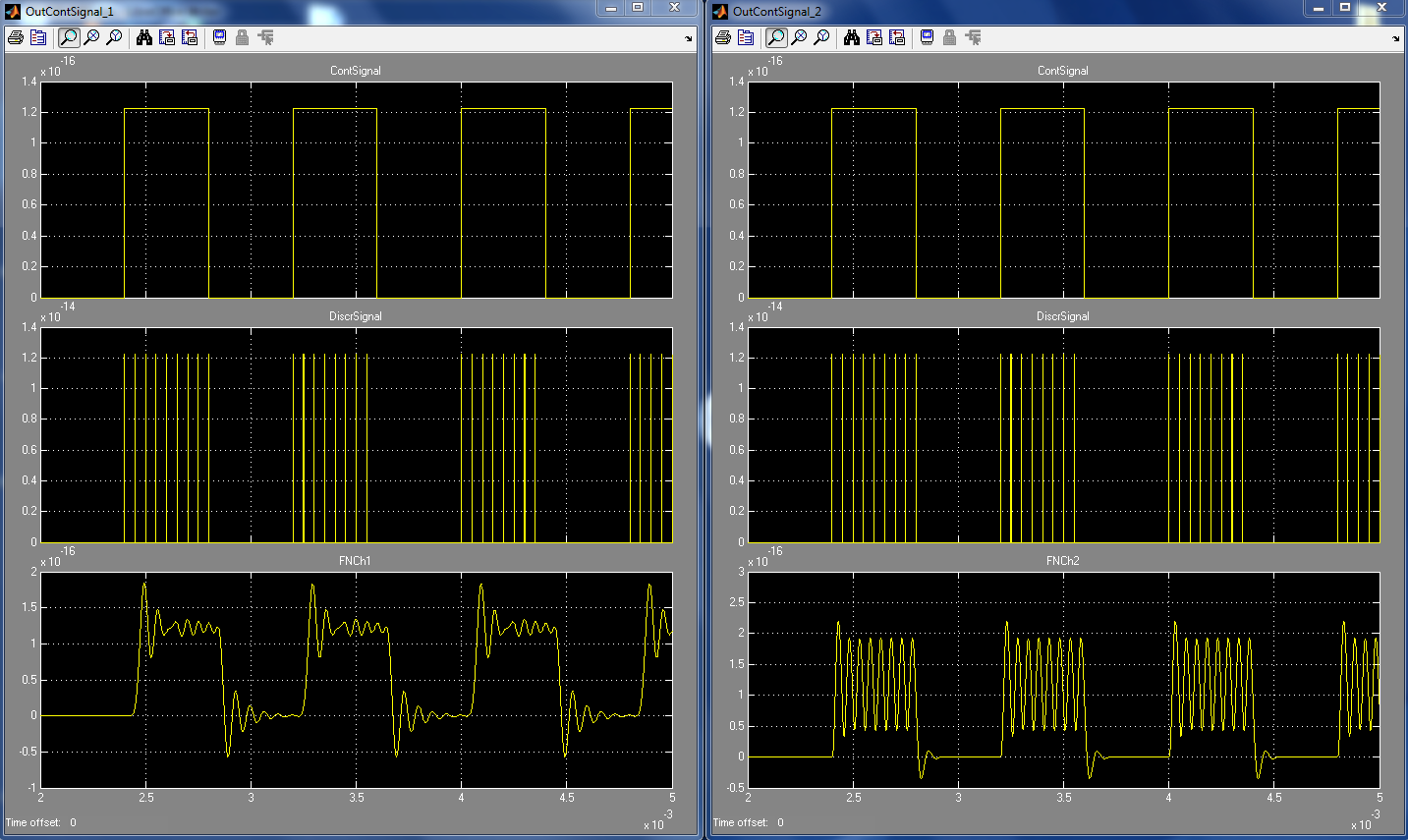
График исследования процесса дискретизации восстановления
радиоимпульсов fд = 40 кГц
1.6 Скачать любимую музыкальную композицию и открыть ее в программе audacity. Вырезать фрагмент песни длительностью 5 секунд. Разделить стереотрек в моно и задать частоту дискретизации 96 кГц (см. рисунок 5).
1,6.1 Удалить один из треков, чтобы остался один канал звучания (моно). Уве-личить масштаб сигнала, чтобы рассмотреть его вид .
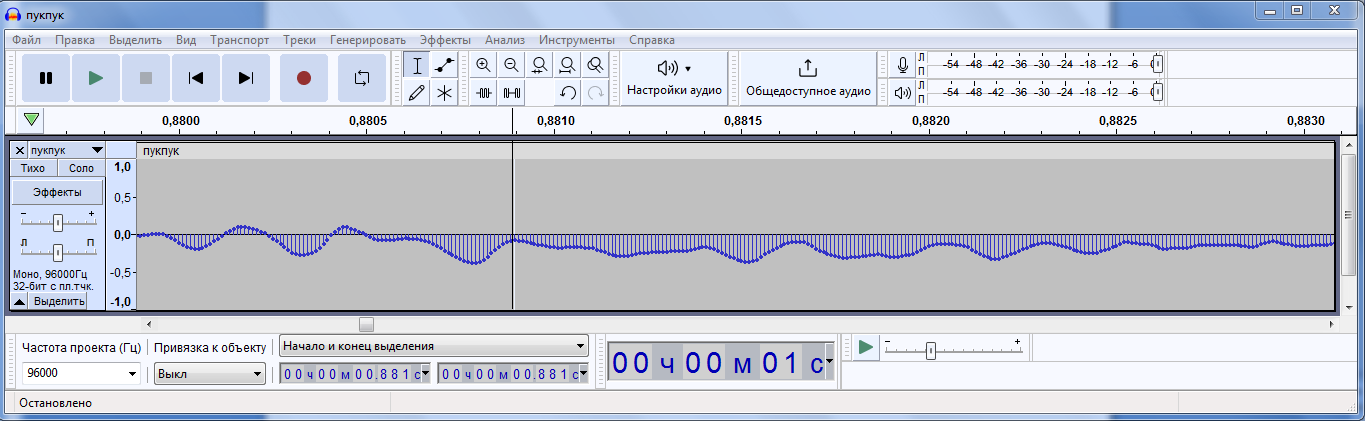
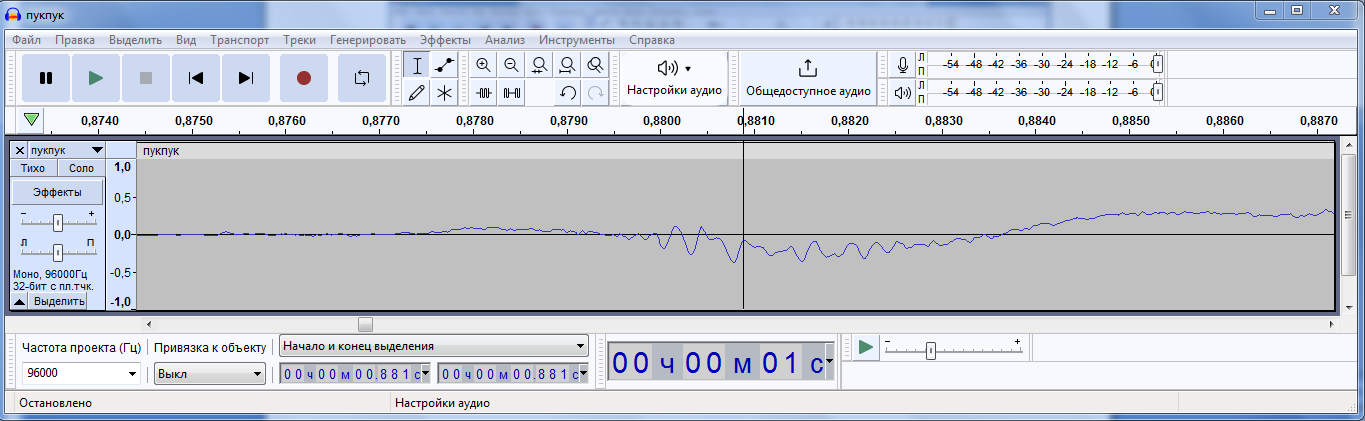
1.6.2 В командном окне ввести код, изменив в нем только название аудиофайла на свой
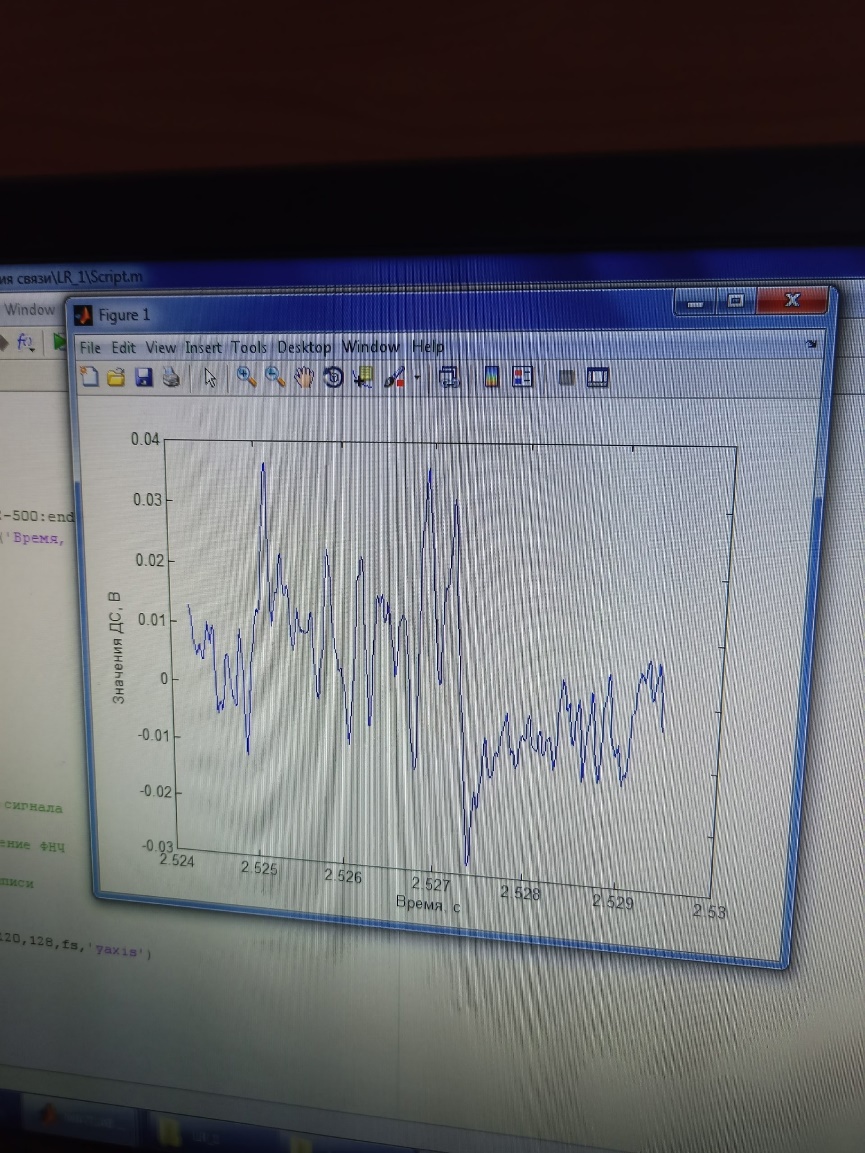
График сигнала
1.6.3 Открыть файл симулинка LR_1_2.slx. Аудио сигнал загружается из Workspace матлаба в Simulink с помощью блока From Workspace. Остальные блоки здесь точно такие же, как в предыдущем задании. Частота дискретизации условно задается в блоке Pulse Generator1 и должна быть равна = 48 кГц. Выставить частоту среза фильтра 2*pi*25e3 и после запуска симуляции на ос-циллографе Scope3 оценить форму исходного сигнала, результат дискретизации и результат восстановления сигнала с помощью фильтра Батерворта ФНЧ 4 по-рядка.
1.6.4 Изменять частоту дискретизации в блоке Pulse Generator1 в соот-ветствии со значениями в таблице. Оценить степень искажения сигнала из-за уменьшения частоты дискретизации визуально по осциллограммам в модели Simulink и на слух (используйте код ниже таблицы). Записать комментарии или оценки по качеству восстановленного сигнала в таблицу.
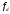 , кГц , кГц | 48 | 24 | 8 | 4 | 2 |
| Схожесть сигналов по графику | | | | | |
5.6.6 Построить спектрограмму сигнала
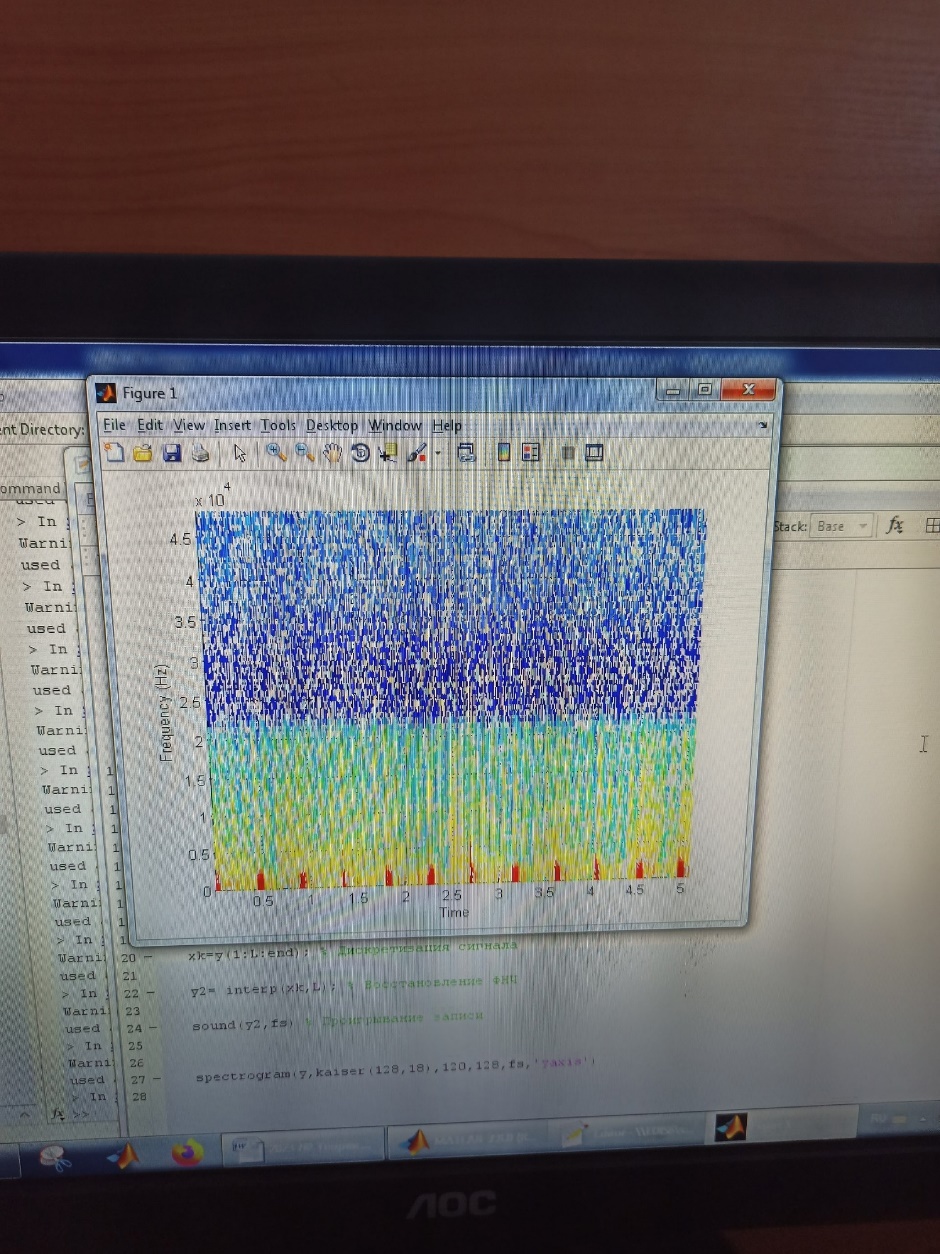
Спектрограмма сигнала
5.6.7 Сравнить спектрограмму сигнала с графиками спектра фрагментов сигнала и спектра сигнала всей длительности.
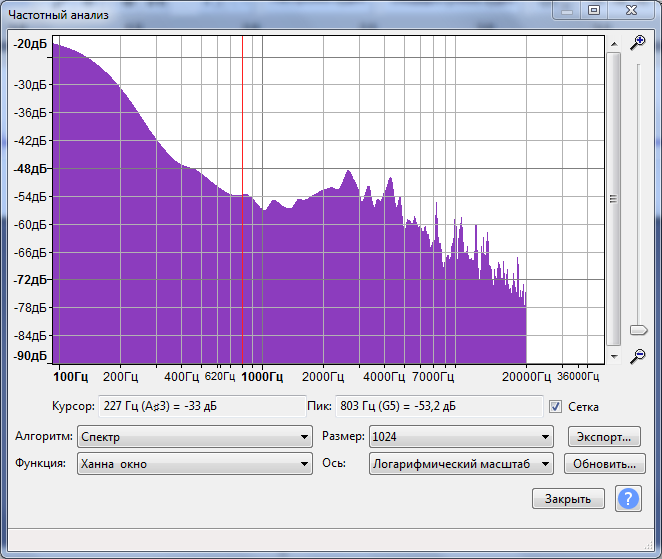
График спектр сигнала
Вывод: Были изучены процессы временной дискретизации аналоговых сигналов и их последующее восстановление с помощью фильтра нижних частот (ФНЧ).