ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Глава 4. Системы рациональных уравнений
Четвёртая глава посвящена изучению способов решения систем рациональных уравнений. Здесь используются понятия, изученные в 7 классе и применявшиеся ранее к системам линейных уравнений, что даёт возможность повторить изученное и научится действовать в новой ситуации. Это понятия: решения уравнения с двумя (тремя) неизвестными, системы уравнений с двумя (тремя) неизвестными, понятие равносильности уравнений, систем уравнений.
Цель изучения главы 4: усвоить перечисленные понятия, научиться решать системы рациональных уравнений и применять их к решению текстовых задач.
§ 9. Системы рациональных уравнений
Основная цель девятого параграфа заключается в том, чтобы, опираясь на известные понятия, связанные с уравнениями и системами линейных уравнений, научится решать системы рациональных уравнений, научиться применять их к решению текстовых задач.
9.1. Понятие системы рациональных уравнений
В данном пункте вводятся понятия рационального уравнения с двумя (тремя) неизвестными и его решения, определяется, что значит решить систему уравнений, приводятся утверждения о равносильности систем уравнений.
Основными заданиями данного пункта являются задания на установление того, что данная пара (тройка) чисел является решением системы. Дополнительное задание приучает учащихся к решению задач с параметрами.
Задание для повторения. При изучении данного пункта можно использовать задание 805–807.
Решения и комментарии
500. Является ли решением системы уравнений
пара чисел:а) (0; 3); б) (–3; 2).
Решение. а) Так как 0 + 5
3, то пара чисел (0; 3) не является решением второго уравнения системы, а значит, не является и решением системы уравнений.б) Так как –3 + 5 = 2, (–3)2 + (–3)2 – 3 = 0, то пара чисел (–3; 2) является решением системы уравнений.
501. Является ли решением системы уравнений
тройка чисел:а) (1; –1; 1); б) (1; 1; 1).
Решение. а) Так как 1 – 1 + 1
3, то тройка чисел (1; –1; 1) не является решением первого уравнения системы, а значит, не является и решением системы уравнений.б) Так как 1 + 1 + 1 = 3, 1 –1 – 1
–2, то тройка чисел (1; 1; 1) не является решением второго уравнения системы, а значит, не является решением системы уравнений.Дополнительное задание
1. При каком значении a пара чисел (2; –1) является решением системы уравнений
Решение. Пусть a — некоторое число, для которого пара чисел (2; –1) является решением системы уравнений, тогда верны два числовых равенства:
1) 2a2 + a = 21 и 2) 10 + a = a2 + 4,
которые можно рассматривать как уравнения относительно a. Уравнение 2) имеет два корня: a1 = 3 или a2 = –2. Число a1является корнем уравнения 1), а число a2 = –2 — нет, следовательно, при a = 3 пара чисел (2; –1) является решением системы уравнений. И других значений а, удовлетворяющих условию задачи, нет.
9.2. Способ подстановки решения систем рациональных уравнений
В данном пункте на трёх примерах показано, как можно решать способом подстановки рациональных уравнений, в которых имеется хотя бы одно уравнение первой.
Задание для повторения. При изучении данного пункта можно использовать задание 810.
Решения и комментарии
512. Решите систему уравнений:
г)
д) 
Решение. г) Выразив x через y из второго уравнения системы и подставив y + 1 вместо x в первое уравнение, перепишем систему в виде:
(1)Теперь, решив первое уравнение системы (1), найдём два его корня y1 = –4 и y2 = 3. Из второго уравнения системы (1) получим соответствующие им значения x: x1 = –3 и x2 = 4.
д) Выразив y через x из второго уравнения системы и подставив 3 – 3x вместо y в первое уравнение, перепишем систему в виде:
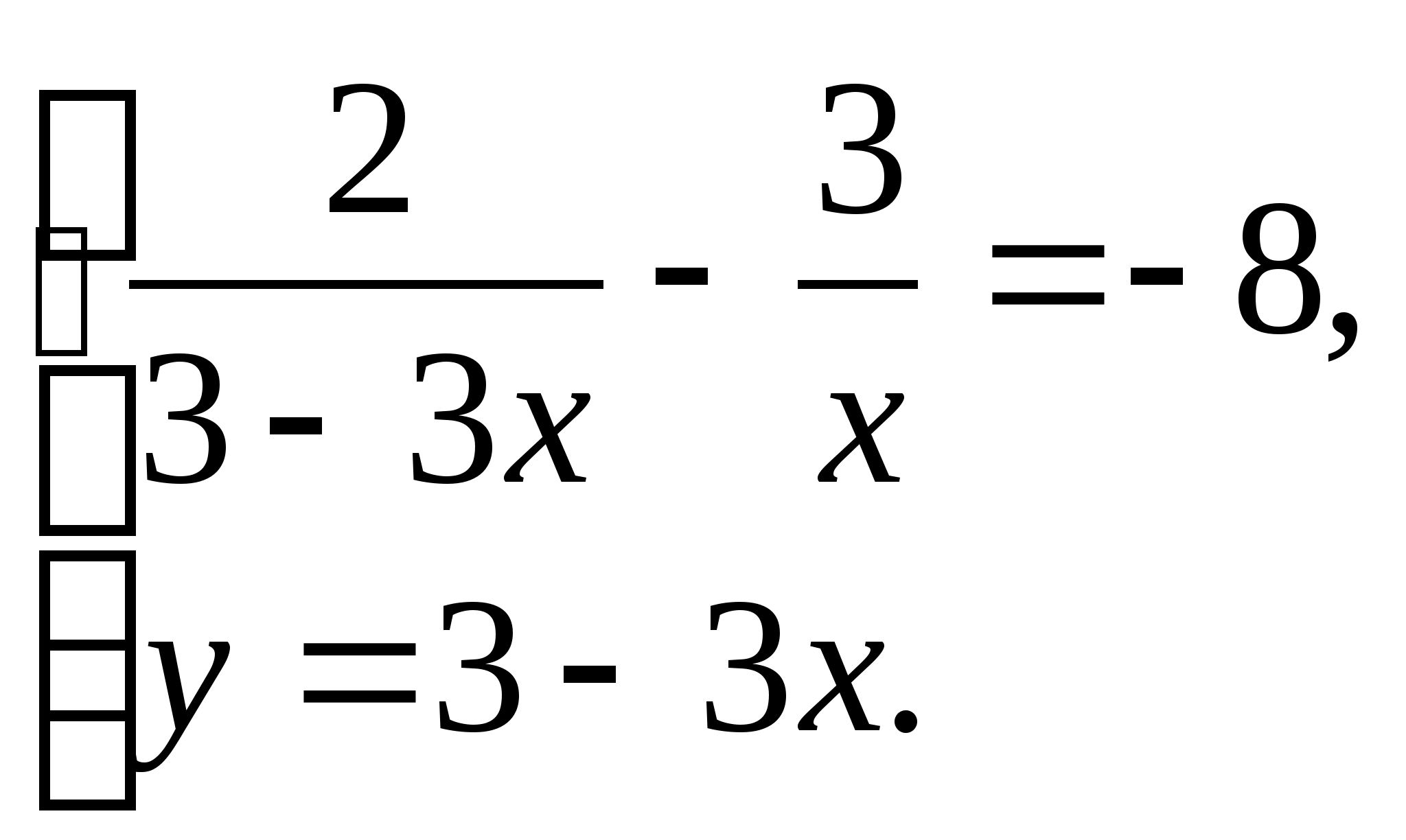(2)Теперь, решив первое уравнение системы (2), найдём два его корня x1 =
и x2 =
. Из второго уравнения системы (2) получим соответствующие им значения y: y1 = –
и y2 = 2.Ответ. г) (–3; –4), (4; 3); д) (
; – ), ( ; 2).Промежуточный контроль. С-21.
9.3. Другие способы решения систем рациональных уравнений
В данном пункте разобраны примеры решения систем рациональных уравнений — способом сложения уравнений, способом введения новых неизвестных, способом выделения полных квадратов, способом разложения на множители. При этом используются равносильные преобразования уравнений. Иногда решению системы помогает знание того, что сумма квадратов двух чисел равна нулю тогда и только тогда, когда эти числа нули.
Задание для повторения. При изучении данного пункта можно использовать задание
820.
Решения и комментарии
517. Решите систему уравнений:
в)
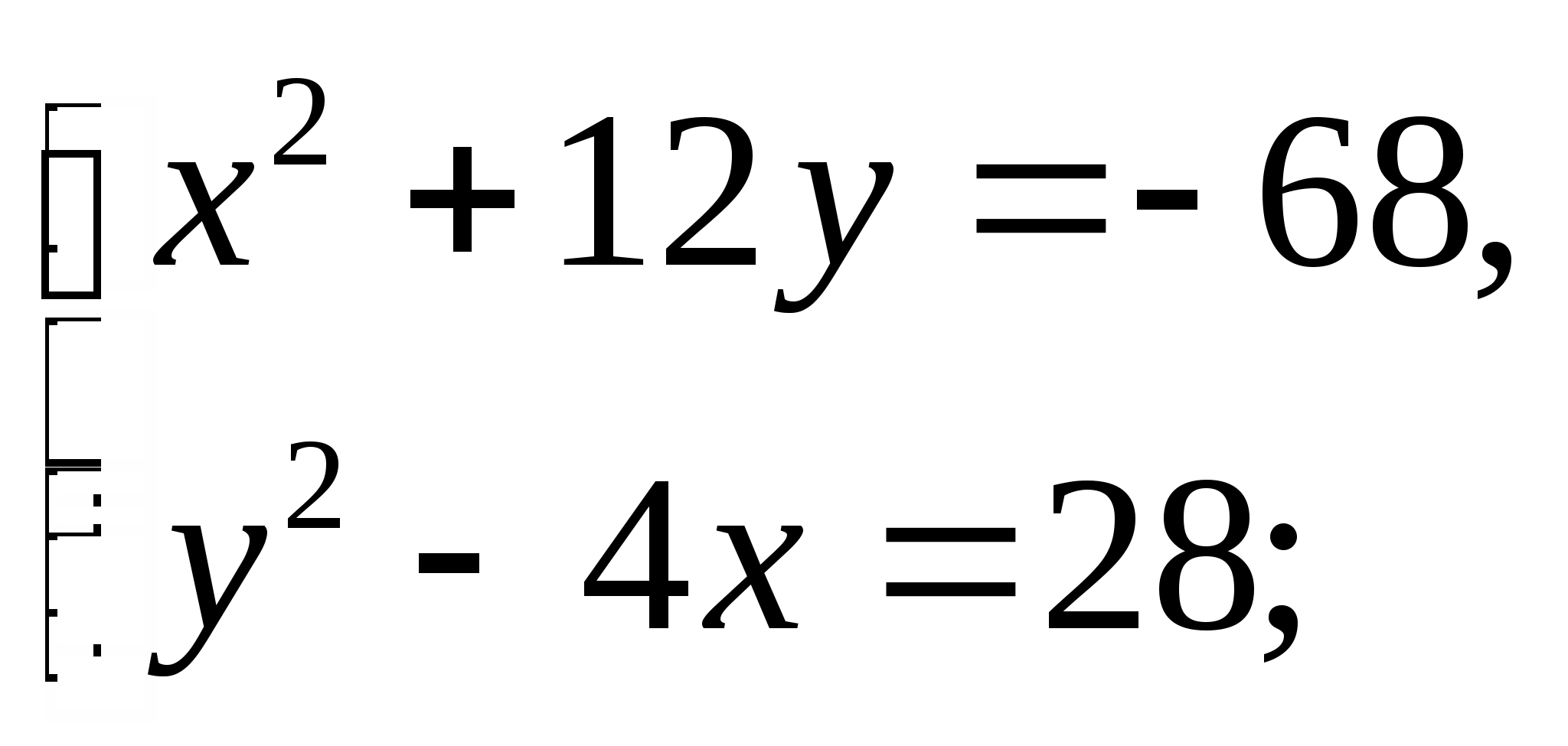д) 
Решение. в) Заменим в системе первое уравнение суммой двух уравнений этой системы. Получим систему, равносильную исходной системе:
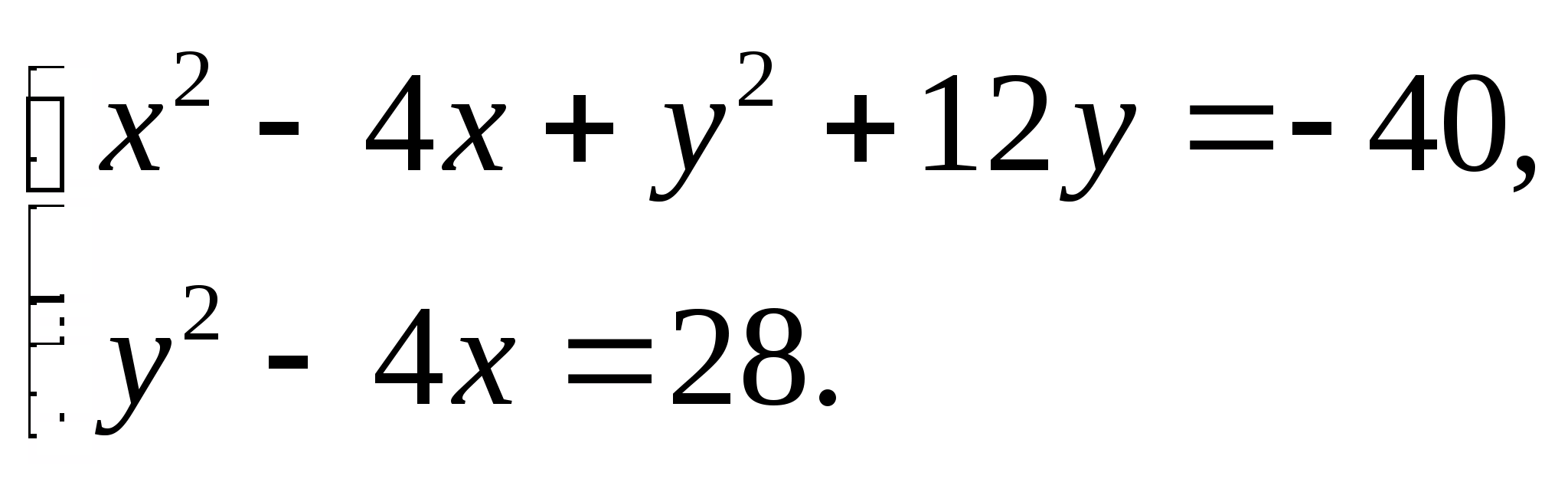(1)Теперь выделим полные квадраты в первом уравнении системы (1):
(2)Так как сумма квадратов двух чисел равна нулю тогда и только тогда, когда эти числа нули, то первое уравнение системы (2) имеет единственное решение (2; –6). Эта пара чисел является решением второго уравнения системы (2), следовательно, она является решением системы (2) и равносильной ей исходной системы.
д) Сделаем замену неизвестных: a =
и b = 
. Перепишем систему в виде:
(3)Система (3) имеет единственное решение: a1 = 1, b1 =
. Следовательно, система д) также имеет единственное решение: x1 = 1, y1 = 2.Ответ. в) (2; –6); д) (1; 2).
512. ж) Решите систему уравнений
Решение. Обычно решение такой системы записывают, заменяя данную систему равносильными ей системами:
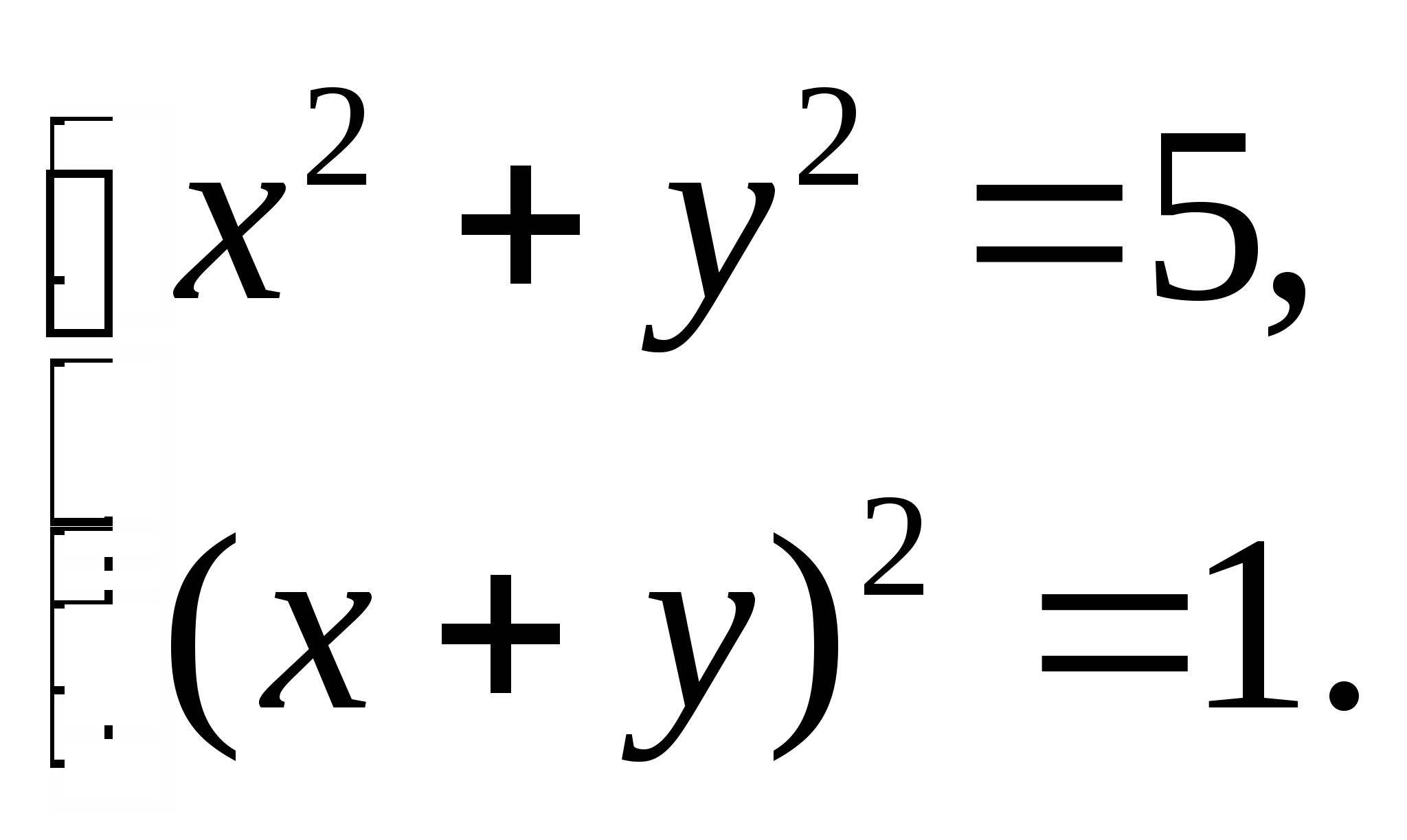(4)Знаки равносильности (
) поставлены для учителя, но в классе с углублённым изучением математики его вполне можно использовать.Решениями второго уравнения последней из систем (4) являются такие пары чисел (x; y), которые являются решениями хотя бы одного из уравнений:
1) x + y = 1 и 2) x + y = –1.
Поэтому все решения исходной системы есть объединение всех решений двух систем:
3)
и 4) 
Решив системы 3) и 4) получим все решения исходной системы: (–1; 2), (2; –1), (1; –2), (–2; 1).
Ответ. (–1; 2), (2; –1), (1; –2), (–2; 1).
518. Решите систему уравнений:
а)
в) 
ж) 
Решение. а) Введя новое неизвестное a = x2 – 4y, перепишем первое уравнение системы в виде:
. Оно имеет единственный корень a = 1. Это означает, что данная система равносильна системе
(5)Сложив уравнения системы (5) и заменив полученным уравнением первое уравнение системы, получим новую систему, равносильную системе (5), а значит, и исходной системе:
(6)Выделив в первом уравнении системы (6) полные квадраты, перепишем систему (6) в виде:
(7)Теперь очевидно, что первое уравнение системы (7) имеет единственное решение: x1