Файл: Сабаты таырыбы Квадратты функция оларды асиеттері мен графиктері Осы сабата ол жеткізілетін оу масаттары.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Тексерілді: | Мектеп: | |
| Күні: | Мұғалім: | |
| Сынып:8 | Қатысқандар саны: | Қатыспағандар саны : |
| Сабақтың тақырыбы: | Квадраттық функция. олардың қасиеттері мен графиктері | |
| Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасын сілтеме) | 8.4.1.2 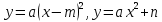 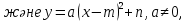 түрдегі квадраттық функциялардың қасиеттерін білу және графиктерін салу;8.4.1.4 аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу; | |
| Сабақ мақсаты: | Барлық оқушылар: Функциялар, олардың қасиеттері мен графиктері арқылы тақырыпты меңгереді және білімдерін бекітеді, оны есептер шығаруда пайдаланады Оқушылардың басым бөлігі: Квадраттық функция графигінің жалпы түрін және оның графигін салу алггоритмімен таныстыру. Белгілі графиктердің көмегімен және алгоритм бойынша квадраттық функцияның графигін салуды үйрету. Кейбір оқушылар: Квадраттық функция тарауы бойынша оқушылар білімдерін пысықтайды, жүйелейді, тиянақтайды және толықтырады. | |
Сабақтың барысы
| Сабақтың кезеңі | Педагогтың әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | ||||||
| Сабақтың басы | Сабағымызды бастамас бұрын өткенді қайталап алайық. . Жаңа сабаққа деген қызығушылықтары оянып,ерекше ынтамен кіріседі. Қайталау: «миға шабуыл» стратегиясы бойынша өткенді пысықтау. | «Сұхбаттасатын жұп» бойынша үй тапсырмалары тексеріледі. 1. Функция дегеніміз не? 2. Аргумент дегеніміз не? 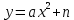 функциясының графигіну=ах2 функциясының графигінен қалайаламыз? . 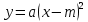 функциясының графигіну=ах2 функциясының графигінен қалайаламыз? 1-топ. Координаталық жазықтық ұғымы. Функция дегеніміз не? 2-топФункцияның графигі деген не?
| Оқушылардың белсенділіген байланысты бағаланады. | | ||||||
| Сабақтың ортасы | 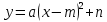 түріндегі квадраттық функцияның графигі«Ой қозғау»: 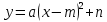функциясының графигін салу үшін қандай функциялардың графигін пайдалануға болады деп ойлайсыңдар?(Оқушылар жауабын тыңдау)(Жауап: у = аx2, у = аx2 + n, y = a (x – m)2 функцияларының графиктерін пайдалануға болады.) у=а(х-m)2+n функциясының графигін салу үшіну=ах2 функциясының графигін Ох осі бойымен m>0 болғанд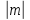а  бірлікке оңға; m<0 болғанд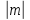а бірлікке солға; Оу осі бойымен n>0 болғанда 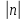 бірлікке жоғары n<0 болғанда 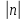бірлікке төмен жылжытамыз Парабола тармағы а>0 болғанда жоғары; а<0 болғанда төмен қарайды. Графигі төбесі (m;n) болатын парабола шығады. | у=х2 функциясының графигін координаталық оське параллель жылжытып, әрбір жағдай үшін берілген функцияны жазыңдар. а) 3 бірлік оңға және 2 бірлік жоғары; у=(х-3)2+2 ә) 1 бірлік солға және 3 бірлік жоғары; у=(х+1)2+3 б) 5 бірлік оңға және 4 бірлік төмен у=(х-5)2-4 Берілген графиктер бойынша формулаларды жазып,түсінік беру: Жауаптары: а) у=(х+3)2+2 ә) у=(х-2)2+1 б) у=(х+1)2-2 Берілген функцияның графигін у=х2 функциясының графигінен қалай алуға болады? а) у=(х-2)2+1 ә) у=(х+1)2-4 б) у=(х-3)2-4 Дескриптор
| Оқушылардың белсенділіген байланысты бағаланады. | | ||||||
| Сабақтың соңы | РАФТ» әдісін пайдаланып, оқушыларға сызықтық функция тақырыбына шығармашылық есептер құрастыру. /Топ бойынша құрастыру./ Мына кестеден берілген функциялардың графигін дұрыс анықтағанда, әр парабола төбесіндегі әріптерден қандай сөз шығады? Ол нені білдіреді? а) y = - x ²; ә) y = (x+5) ² б) y = -(x - 3) 2 +4; в) y =(x+4) 2 – 4 г) y = -(x + 2) 2 +3; д) y = -(x - 6) 2 е) y = x2 +2 | 1 - есеп: а - ның қандай мәндерінде у=ах2 - 16х+1 параболасының симметрия осі х=4 түзуі болады? Жауабы: а=2 2 - есеп: в - ның және с - ның қандай мәндерінде у=х2 - 6х+с параболасының төбесі (6; - 12) нүктесі болады? Жауабы: в=- 12, с=24 3 - есеп: у=ах2+вх - 18 функциясының графигі М(1; 2) және N(2; 10) нүктелері арқылы өтетіндей а - ның және в - ның мәндерін табыңдар. Жауабы: а=- 6, с=26. | Оқушылардың белсенділіген байланысты бағаланады. | |
0>0>0>