ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Этапы эконометрического моделирования Выделяют следующие этапы: постановочный; априорный; спецификация модели; информационный; идентификация модели; верификация модели; интерпретация результатов.
Причины наличия в регрессионной модели случайного отклонения. Среди таких причин можно выделить наиболее существенные: не включение в модель всех объясняющих переменных, неправильный выбор функциональной формы модели, агрегирование переменных, ошибки измерений, ограниченность статистических данных, непредсказуемость человеческого фактора.
Типы моделей и переменных, применяемых в эконометрике. Чем регрессионная модель отличается от функции регрессии?
Для моделирования эконометрических взаимосвязей между экономическими явлениями чаще всего применяется три типа моделей и три типа переменных.
Типы моделей:
1) Модели временных рядов - Модель представляет собой зависимость результативного признака от переменной времени или переменных, относящихся к другим моментам времени.
2) Модели регрессии - это уравнение, в котором объясняемая переменная представляется в виде функции от объясняющих переменных (например, модель спроса на некоторый товар в зависимости от его цены и дохода покупателей).
3) Системы одновременных уравнений - системы уравнений, состоящие из регрессионных уравнений и тождеств, в каждом из которых помимо объясняющих – независимых – переменных содержатся объясняемые переменные из других уравнений системы.
Типы переменных:
1) Экзогенные (внешние, независимые)- это внешние для модели переменные, управляемые из вне, влияющие на эндогенные переменные, но не зависящие от них. Х-обознач.
2) Эндогенные (внутренние, зависимые)- это внутренние, формируемые в модели переменные, зависимые от предопределенных переменных. Y-обоз.
3) Предопределенные (экзогенные и лаговые эндогенные)-называют экзогенные переменные
х и лаговые эндогенные переменные yt-l.
Регрессионная модель – это уравнение, в котором объясняемая переменная представляется в виде функции от объясняющих переменных.
Функция регрессии –функция f(x1,x2..)описывает зависимость условного среднего значения результативной переменной y от заданных объясняющих переменных.
Суть метода наименьших квадратов (мнк). Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данныха и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных. Вывод формул для нахождения коэффициентов. Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции по переменныма и b, приравниваем эти производные к нулю
Предпосылки МНК: 1 - случайный характер остатков; 2 - гомоскедастичность – дисперсия остатков одинакова для всех значений фактора; 3 - отсутствие автокорреляции остатков (то есть остатки распределены независимо друг от друга); 4 - остатки подчиняются нормальному закону распределения.
Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений)
Баланс для сумм квадратов отклонений результативного признака.
или Q = Qr + Qe, где Q – общая сумма квадратов отклонений зависимой переменной от средней, Qr и Qe – соответственно, сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтённых факторов.
Общая СКО равна факторной, когда прочие факторы не влияют на результат, y связан с x функционально, и остаточная СКО равна нулю.
, Нулевая гипотеза принимается, если . Проверка гипотез об общем статистическом
качестве модели множественной линейной регрессии. (1) Гипотеза о статистической незначимости коэффициента детерминации . , где – значение критической точки распределения Фишера при уровне значимости и значениях степеней свободы , . (2) Гипотеза о равенстве двух коэффициентов детерминации вложенных моделей. Пусть для выборке из n наблюдений получено уравнение регрессии вида. , (А). и коэффициент детерминации для этой модели равен . Исключим из рассмотрения k экзогенных переменных, предположив, не нарушая общности, что это переменные при последних k коэффициентах
Использование критерия Стьюдента для проверки значимости параметров регрессионной модели
Проверка статистической значимости параметров регрессионного уравнения (коэффициентов регрессии) выполняется по t-критерию Стьюдента, который рассчитывается по формуле:
где P - значение параметра;
Sp - стандартное отклонение параметра.
Рассчитанное значение критерия Стьюдента сравнивают с его табличным значением при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели Y=A*X+B подставляем k=1).
Если вычисленное значение tp выше, чем табличное, то коэффициент регрессии является значимым с данной доверительной вероятностью. В противном случае есть основания для исключения соответствующей переменной из регрессионной модели.
Величины параметров и их стандартные отклонения обычно рассчитываются в алгоритмах, реализующих метод наименьших квадратов.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. Согласно F-критерию Фишера, выдвигается «нулевая» гипотеза H0 о статистической незначимости уравнения
регрессии и показателя тесноты связи. Непосредственному расчету F-критерия предшествует анализ дисперсии. Наблюдаемые значения результативного признака yi можно представить в виде суммы двух составляющих ŷi и εi: yi = ŷi+ εi. Из данного уравнения следует следующее соотношение между дисперсиями наблюдаемых значений переменной D(y), ее расчетных значений D(ŷ) и остатков D(е) (остаточной дисперсией Dост = D(ε))
Статический смысд Коэффициент детерминации - это статистическое измерение, которое исследует, как различия в одной переменной могут быть объяснены различием во второй переменной при прогнозировании исхода данного события. Другими словами, этот коэффициент, более известный как r-квадрат (или r2), оценивает, насколько сильна линейная зависимость между двумя переменными, и на него в значительной степени полагаются инвесторы при проведении анализа тренда.
Какова связь между линейным коэффициентом корреляции и коэффициентом регрессии в линейной модели парной регрессии?
⇐ ПредыдущаяСтр 3 из 10
коэффициент детерминации рассчитывается как квадрат линейного коэффициента корреляции r 2. Он характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака:
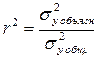
Величина коэффициента детерминации служит одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов, и, следовательно, линейная модель хорошо аппроксимирует исходные данные и ею можно воспользоваться для прогноза значений результативного признака
При линейной регрессии в качестве показателя тесноты связи выступает линейный коэффициент корреляции
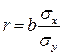. Коэффициент регрессии показывает, на сколько единиц в среднем изменится У, когда Х увеличивается на одну единицу. Однако он зависит от единиц измерения переменных. Как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой.
Имеется следующая гипотетическая структурная модель:
Y1 = b12Y2 + a11X1 + a12X2
Y2 = b21Y1 + b23Y3 + a22X2
Y3 = b32Y2 + a31X1 + a33X3
Приведенная форма модели имеет вид:
Y1 = 3X1 - 6X2 + 2X3
Y2 = 2X1 + 4X2 + 10X3
Y3 = -5X1 + 6X2 +5X3
Требуется проверить структурную форму модели на идентификацию проверить структурную форму модели на идентификацию.
Решение:
Для того чтобы система одновременных уравнений была идентифицируема, необходимо, чтобы каждое уравнение системы было идентифицируемо, т.е. выполнялись необходимое и достаточное условия идентификации.
Необходимое условие идентификации можно записать в виде следующего счетного правила:
* если D+1<Н, то уравнение неидентифицируемо;
* если D+1=Н, то уравнение идентифицируемо;
* если D+1>Н, то уравнение сверхидентифицируемо,
где Н - число эндогенных переменных в уравнении; D - число предопределенных переменных, которые содержатся в системе уравнений, но не входят в данное уравнение.
Достаточное условие идентификации для данного уравнения выполнено, если определитель полученной матрицы не равен нулю, а ранг матрицы не меньше, чем количество эндогенных переменных в системе без одного.
Проверим первое уравнение системы Y1 = b12Y2 + a11X1 + a12X2 на выполнение необходимого и достаточного условия идентификации.
В этом уравнении две эндогенные переменные Y1 и Y2 (Н=2). В нем отсутствуют эндогенная переменная Y3 и экзогенная переменная X3 (D=2). Уравнение сверхидентифицируемо, т.к. D+1>H; (3>2), а значит необходимое условие идентификации выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Y3 и X3, взятых в других уравнениях.
| | | |
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| У3 | Х3 | |
| 2 | b23 | 0 |
| 3 | -1 | a33 |