Файл: Этапы эконометрического моделирования.docx

Скачать файл (0,70Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.12.2023

Просмотров: 24

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Определитель полученной матрицы не равен нулю, т.к. b23*a33 - (-1)*0 = 0, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и первое уравнение идентифицируемо.

Проверим второе уравнение системы Y2 = b21Y1 + b23Y3 + a22X2 на выполнение необходимого и достаточного условия идентификации.

В этом уравнении три эндогенные переменные Y1, Y2 и Y3 (H=3). В нем отсутствуют две экзогенные переменные X1 и X3 (D=2). Уравнение идентифицируемо, т.к. D+1=H; (3=3), а значит необходимое условие идентификации выполнено.

, взятых в других уравнениях.


Уравнения, из которых взяты коэффициенты при переменных	Переменные
х1	х3
1	a11	0
3	a31	a33

Определитель полученной матрицы не равен нулю, т.к. a11*a33 - a31*0 = 0, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и второе уравнение идентифицируемо.

Проверим третье уравнение системы Y3 = b32Y2 + a31X1 + a33X3 на выполнение необходимого и достаточного условия идентификации.

В этом уравнении две эндогенные переменные Y2 и Y3 (H=2). В нем отсутствуют эндогенная переменная Y1 и экзогенная переменная X2 (D=2). Уравнение сверхидентифицируемо, т.к. D+1>H; (3>2), а значит необходимое условие идентификации выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Y1 и X2, взятых в других уравнениях.


Уравнения, из которых взяты коэффициенты при переменных	Переменные
У1	Х2
1	-1	a12
2	b21	a22

Задача 1.Зависимость объема продаж (Y) от расходов на рекламу (X) характеризуется по 12 предприятиям концерна следующим образом:

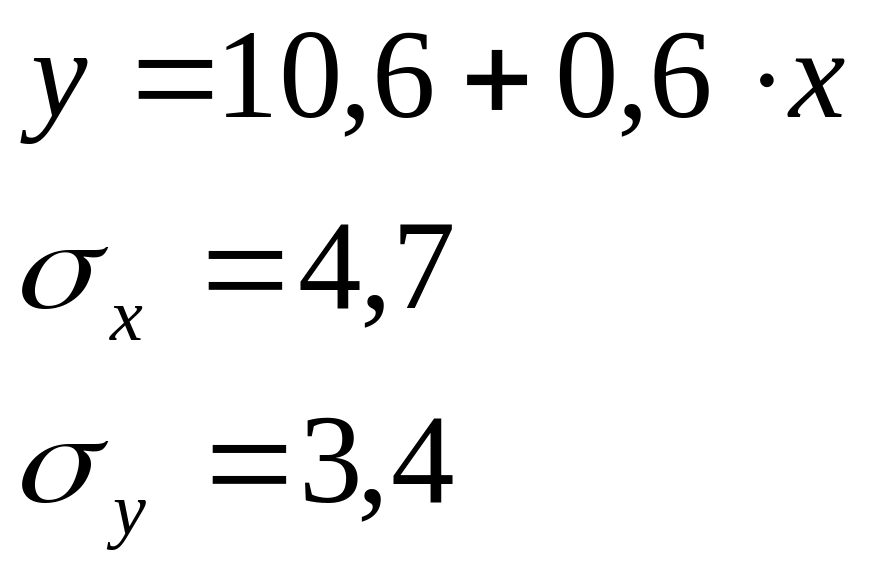
Задание: определите линейный коэффициент парной корреляции, регрессионную сумму квадратов отклонений, постройте таблицу дисперсионного анализа для оценки значимости уравнения в целом, определите F-статистику, t-статистику и доверительный интервал коэффициента регрессии.

Решение:

Для определения коэффициента корреляции применим формулу:

Значение коэффициента корреляции свидетельствует о тесной линейной взаимосвязи между объемом продаж и расходами на рекламу.

Коэффициент детерминации составит:

Определим регрессионную сумму квадратов отклонений:

Составим таблицу дисперсионного анализа и определим F-cтатистику Фишера.

Дисперсионный анализ результатов регрессии

Источники вариации	Число степеней свободы	Сумма квадратов отклонений	Дисперсия на одну степень свободы	F-статистика
				факт.	табл., α=0,05
Регрессионная (объясненная)	1	87,359	87,359	21,949	4,96
Остаточная	10	39,801	3,9801
Общая	11	127,16	11,56

Поскольку F_факт >F_табл, то признается статистическая значимость, надежность уравнения регрессии.

Связь между F-статистикой Фишера, t-статистикой Стьюдента для коэффициента регрессии, t-статистикой Стьюдента для коэффициента корреляции выражается равенством:

Значит,

. Табличное значение t-статистики для α=0,05, v=10 составляет 2,2281. Поскольку t_факт>t_табл, то коэффициент регрессии b статистически значимо отличен от нуля.

Экономическая интерпретация параметров линейной модели парной регрессии.

Экономический смысл свободного коэффициента Параметр а, или свободный коэффициент регрессионного уравнения, имеет экономический смысл: он показывает значение результативного признака y, если факторный x = 0.

b — коэффициент регрессии. Показывает, на какую величину в среднем изменится y при увеличении фактора х на 1 единицу.

8.Модели нелинейной регрессии, коэффициент эластичности

Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция:

Связано это с тем, что параметр bв ней имеет четкое экономическое истолкование, т. е. он являетсякоэффициентом эластичности. Это значит, что величина коэффициента bпоказывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %.

Например, если зависимость спроса от цен характеризуется уравнением вида

, то с увеличением цен на 1 % спрос снижается в среднем на 1,12 %.

В силу того, что коэффициент эластичности для нелинейной функции не является величиной постоянной, а зависит от соответствующего значения

х, то обычно рассчитывается средний показатель эластичностипо формуле:

Поскольку коэффициенты эластичности представляют экономический интерес, а виды моделей не ограничиваются только степенной функцией, приведем формулы расчета коэффициентов эластичности для наиболее распространенных типов уравнений регрессии.

Коэффициенты эластичности по разным видам регрессионных моделей.

1.Линейная