Файл: Задача Найти матрицу, обратную матрице . Решение. Находим определитель.doc
Добавлен: 06.12.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
Задача 1. Найти матрицу, обратную матрице
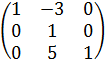 .
.Решение.
Находим определитель.
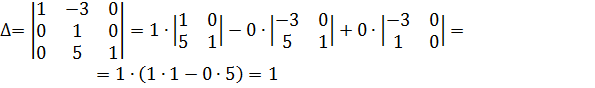
Определитель отличен от нуля, так что матрица А обратима.
Найдем матрицу из алгебраических дополнений:
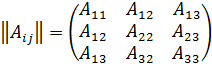
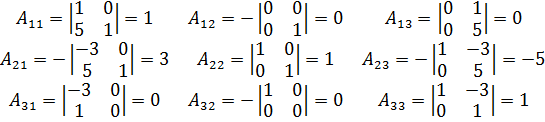
Поэтому:
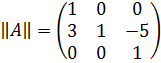
Выполним транспонирование матрицы из алгебраических дополнений:
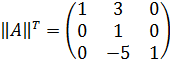
Теперь находим обратную матрицу:
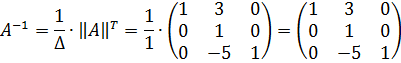
Задача 2. Решить СЛАУ
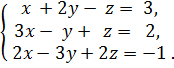
Решение.
Решим систему методом Гаусса. Для этого запишем расширенную матрицу системы, а затем вычтем первое уравнение из второго и третьего, и второе из третьего.
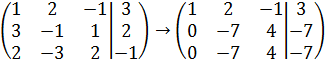
Так после преобразований второе и третье уравнения идентичны, то система сводится к двум уравнениям с тремя неизвестными. Найдем множество решений или докажем что их нет.
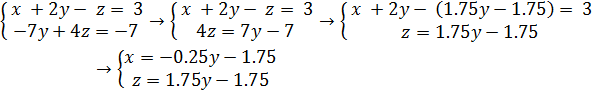
Неизвестная y может принимать любое числовое значение а. Таким образом множество решений системы:
Задача 3. Вероятность того, что в результате проверки изделию будет присвоен «Знак высшего качества», равна 0,2. На контроль поступило 9 изделий. Какова вероятность того, что знак высшего качества будет присвоен:
а) ровно 6-ти изделиям;
б) более чем 7-ми изделиям;
в) хотя бы одному изделию;
г) указать наивероятнейшее число изделий, получивших знак высшего качества, и найти соответствующую ему вероятность.
Решение.
Имеем схему Бернулли с параметрами p=0,2 (вероятность того, что изделию будет присвоен «Знак высшего качества»), n=9 (количество изделий на контроле), q=1 – p = 1 – 0.2 = 0.8 (противоположная вероятность). Будем использовать формулу Бернулли:
а) вероятность присвоения «Знак высшего качества» ровно 6-ти изделиям:
б) вероятность присвоения «Знак высшего качества» более чем 7-ми изделиям:
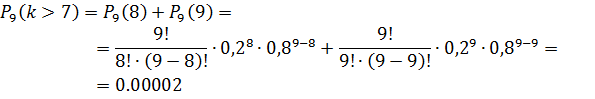
в) вероятность присвоения «Знак высшего качества» хотя бы одному изделию:
г) наивероятнейшее число изделий, получивших знак высшего качества, и соответствующая ему вероятность:
Отсюда следует, что наивероятнейшие количество изделий это 1 и 2, их вероятности равны:
Наивероятнейшие количество изделий - 2, вероятность этого 0,60398