Примеры. Пусть R – радиус шара, Р – любая точка на сфере, а во внутренней точке Р0 помещен единичный заряд1. Функция Грина для шараПусть R – радиус шара, Р – любая точка на сфере, а во внутренней точке Р₀ помещен единичный заряд. 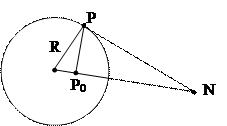 На проводящей сфере индуцируется заряд, потенциал которого равен потенциалу некоторого точечного заряда, помещенного в инверсионном образе N точки Р₀, относительно сферы так, что выполнено равенство:Треугольники ОРР₀ и ОРN подобны (общий угол и стороны пропорциональны).Поэтому   Пусть  Тогда  (10)Действительно,  Очевидно гармонична по Р в замкнутом шаре. 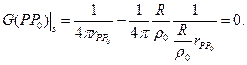Если же точка Р лежит на сфере, тоКак видно из (10) функция Грина для шара есть потенциал электростатического поля, созданный двумя точечными зарядами. 2. Функция Грина для полупространстваВ качестве области ω берем часть, где  Граница S имеет уравнение  В точке  помещаем единичный заряд, который создает поле с потенциалом  .

---

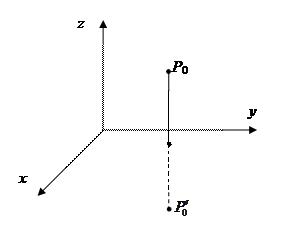
 Внесение проводящей поверхности  приводит к индуцированию зарядов, потенциал которых можно заменить потенциалом отрицательного единичного заряда, помещенного в точку 

Суммарный потенциал



Рассмотрим задачу Дирихле для полупространства  .

 

.

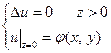Ее решение:









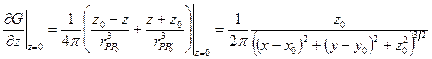
или



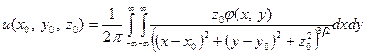
3) Функции Грина для полушара.



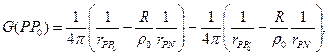
где

 



 

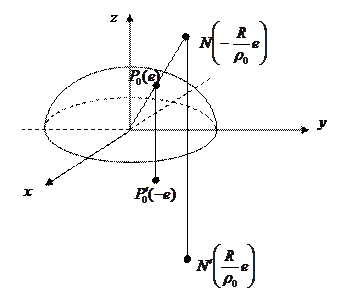
Тема 6. Метод Фурье.

 

Лекция 1. Разделение переменных.

Рассматриваемые вопросы.

1. Решение основных краевых задач методом Фурье.

2. Интеграл Пуассона.

3. Внешняя и внутренняя задачи Дирихле.

 

Пусть ω – круг радиуса R с центром в начале координат, а S – окружность (граница области ω.

Рассмотрим задачу Дирихле

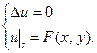 (1)

Перейдем к полярным координатам по формулам

---

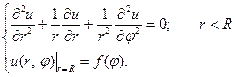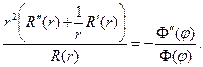
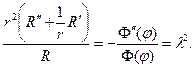
Оператор Лапласа в полярных координатахи задача (1) эквивалентна задаче  (2)Будем искать решение  в виде:Подставим в уравнение ЛапласаилиСледовательно, и левая и правая части этого равенства суть const (можно показать, что эта постоянная положительна)Угловая функция Ф(φ) должна быть периодической. Учитывая это, получим задачу Штурма-Лиувилля. 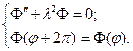 (3)Равенство (3) возможно лишь в случаеДля искомой функции R(r) получаем уравнениеБудем искать решение этого уравнения в виде  , тогдаЕсли же n=0, то  . Как нетрудно проверить имеет своими решениями  и lnr. Таким образом, мы получаем набор функций, гармонических в круге

---

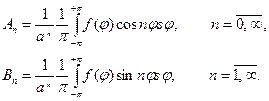
Если предположить, что ряд  (4)можно дифференцировать почленно, то его сумма  также будет гармонической функцией.Подберем коэффициенты этого ряда так, чтобыОтсюда с учетом формул для коэффициентов Фурье следует:Замечание. Ряд (4) очевидно дает общий вид гармонической функции для круга r Угловые функции  и  при этом не использовались, так как они при  разрывны. Вместе с тем, если рассматривать область r>a (внешняя сторона круга), то общий вид гармонической функции для этой области будет задаваться рядом:

 (5)

И, наконец, для кольца 

 (6)

Преобразуем теперь найденные решения к более удобному представлению



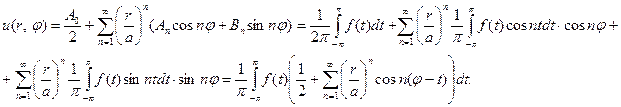
Перестановка операций суммирования и интегрирования законна, так как ряд



сходится равномерно по φ и t нутрии круга r Найдем сумму этого ряда



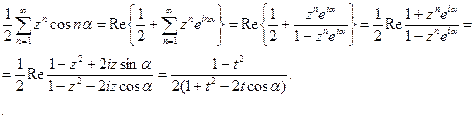
Поэтому

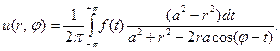 (7)

Представление (7) известно как интеграл Пуассона.

Замечание. Среди двумерных областей, для которых задача Дирихле для уравнений Лапласа решается эффективно методом разделения переменных в декартовых координатах, можно отметить прямоугольник со сторонами параллельными осям координат и в, частности, полуполосу.

 

 

Тема 7. Теория потенциала.

 

Лекция 1. Теория потенциала.

Рассматриваемые вопросы.

1.Объемный и логарифмический потенциалы.

2. Поверхностные потенциалы.

3. Решение основных краевых задач методом потенциала.

 

Некоторые сведения из теории потенциала.

1. Объемный потенциал и его свойства.

Предположим, что в области  распределен электрический заряд с плотностью  Для нахождения потенциала такого электростатического поля разобьем область ω на элементарные части  не имеющие общих внутренних точек. Допустим, что действие заряженной области  равносильно действию точечного заряда  Тогда потенциал электростатического поля в точке наблюдения  можно найти по формуле:



При  очевидно

 (1)

Функцию (1) называют объмным или ньютоновским потенциалом.

Свойство 1. Объемный потенциал есть гармоническая функция по координатам точки  во внешней области  .

Если  то (1) есть обычный тройной интеграл, функция  имеет непрерывные производные любого порядка, интеграл  поэтому производные по  можно вычислять дифференцированием под знаком интеграла. В частности



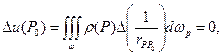
так как 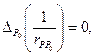 если 

Свойство 2. Объемный потенциал есть непрерывная функция по координатам точки  во всем пространстве 

Действительно, непрерывности в внешности  вытекает из ее гармоничности. Пусть теперь точка  а  есть шар радиуса  с центром в точке  такой, что 

Рассмотрим разность  где точка 



 





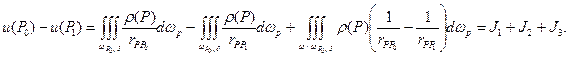
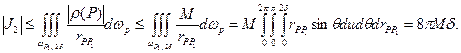
Для  аналогично получаем



Будем считать, что δ фиксировано так, что



Оценим теперь  Если  то выбирая Р₁ достаточно близко к Р₀ получим



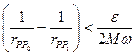
с помощью которого



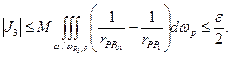
А значит



Непрерывность во внутренних точках области ω объемного потенциала доказана.

Пусть теперь точка  – границе области ω. Рассмотрим более широкую область  и положим 

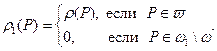
Тогда



и точка Р₀ будет внутренней по отношению к  Следовательно, потенциал в точке Р₀ непрерывен.

Свойство 3. Объемный потенциал имеет непрерывные производные первого порядка в  Доказательство аналогично доказательству свойства 2.

Свойство 4. Если плотность  имеет непрерывные производные первого порядка, то объемный потенциал имеет производные второго порядка в области ω и удовлетворяет уравнению Пуассона



(без доказательства).

Замечание 1. С помощью объемного потенциала решение задачи Дирихле для уравнения Пуассона может быть сведено к решению задачи Дирихле для уравнения Лапласа.

Замечание 2. В двумерном случае роль объемного потенциала играет так называемый логарифмический потенциал



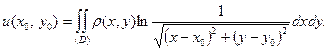
Поверхностные интегралы простого и двойного слоя.
Пусть на некоторой достаточно гладкой поверхности S распределен заряд с плотностью  Тогда потенциал электростатического поля в точке  представляется в виде:

 (2)

Функцию (2) называют потенциалом простого слоя. Перечислим некоторые свойства этого потенциала.

1). Потенциал простого слоя есть гармоническая вне S функция.

2). Потенциал простого слоя есть непрерывная во всем пространстве  функция.

3). Нормальная производная потенциала простого слоя терпит разрыв при переходе через поверхность S.

 

Потенциалом двойного слоя называется выражение



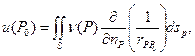
где ν(Р) – есть плотность распределения дипольного момента, а  – внутренняя нормаль к S.

4). Потенциал двойного слоя есть гармоническая вне S функция.

5). Потенциал двойного слоя терпит разрыв при переходе через поверхность S.

6). Потенциал двойного слоя может быть представлен в виде:



Аналогично могут быть введены криволинейные интегралы простого и двойного слоя с аналогичными свойствами.

Замечание. С помощью потенциала двойного слоя решение задачи Дирихле можно свести к решению уравнения Фредгольма второго рода относительно неизвестной функции 

---

Смотрите также файлы

• Дипломная работа функциональные уравнения на оси и полуоси содержание введение.rtf

• В каком году создано управление по надзору за соблюдением прав и свобод граждан в 2006 году в Генеральной прокуратуре рф создано управление по надзору за соблюдением прав и свобод граждан.docx

• Жизнь и творчество Константина Георгиевича Паустовского (18921968гг) Детство.pptx

• Загрузите результат Индивидуального практического задания, слушатель Сафиюллина Динара Наилевна Преподаватель Кусачева Марина Юрьевна.rtf

• Занятие 4 Преподаватель Пермь 2021.docx