Файл: Тема Построение таблиц истинности для логических выражений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
9 класс Информатика Дата ______
Тема:Построение таблиц истинности для логических выражений
Тип урока: комбинированный:
-
проверка знаний – устная работа; -
новый материал – лекция; -
закрепление – практические упражнения; -
проверка знаний – задания для самостоятельной работы.
Цель урока:
Введение понятия Таблица истинности.
Формирование у обучающихся навыков применения технологии построения таблиц истинностидля составных логических выражений.
Задачи урока:
Обучающие:
научить составлять логические выражения из высказываний ;
сформировать знание о таблицах истинности ;
выработать умение применять последовательность действий построения таблиц истинности ;
научить находить значение логических выражений посредством построения таблиц истинности .
Развивающие:
продолжить развитие умения анализировать;
продолжить развитие умения устанавливать причинно-следственные связи;
формировать умения работы с таблицами.
Воспитательные:
совершенствовать навыки общения;
вовлечь в активную деятельность.
План урока:
-
Организационный момент . -
Повторение материала предыдущего урока + проверка домашнего задания (устный опрос) . -
Объяснение нового материала. -
Закрепление
-
разбор примера; -
практические упражнение -
задания для самостоятельной работы .
Обобщение урока, домашнее задание .
Оборудование и программный материал:
-
медиапроектор; -
ПК; -
учебник: Информатика 8, Босова Л.Л. -
доска; -
раздаточный справочный материал “Таблицы истинности”; -
демонстрация презентации “Таблицы истинности”.
Применяемые технологии:
-
Проблемного обучения. -
Личностно-ориентированный подход. -
Здоровьесберегающая. -
ИКТ.
Ход урока
1. Организационный момент
2. Повторение материала предыдущего урока + проверка домашнего задания
Вопросы (Слайд №2)
-
Что такое высказывание? -
Какие бывают высказывания? -
Приведите пример простого высказывания. Сложного высказывания. -
Как обозначаются высказывания в Алгебре логики? -
Чему могут быть равны логические переменные?
(Слайд №3) Джордж Буль – создатель Алгебры Логики.
3. Объяснение нового материала
На предыдущем уроке вы познакомились с понятиями: высказывание, алгебра логики, логические переменные. А сегодня мы рассмотрим основные логические операции, определённые над высказываниями.
Итак, тема сегодняшнего урока: «Построение таблиц истинности для логических высказываний»
Кстати, что же такое таблица истинности? Как вы думаете? (Ученики высказывают свои варианты, учитель резюмирует): (Слайд №4)
Таблица истинности – это таблица, показывающая истинность сложного высказывания при всех возможных значениях входящих переменных.
Но для этого запишем в тетради основные логические операции и разберём таблицы истинности для них.
Послушайте высказывание: «Земля имеет форму шара, который из космоса кажется голубым». Сформулируйте его иначе. Из каких простых высказываний оно состоит?
Итак, у нас появился союз «и». Это связка между простыми высказываниями. Иначе она называется конъюнкция. (Слайд №5)
Конъюнкция – логическая операция, ставящая в соответствие двум высказываниям новое высказывание, которое является истинным тогда и только тогда, когда оба исходных высказывания истинны.
Для записи конъюнкции используются следующие знаки: И, ^, *, &.
Конъюнкцию можно описать в виде таблицы истинности: (см. справочный материал)
| А | В | A&B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Конъюнкцию ещё называют логическим умножением.
Существуют несколько связок между простыми высказываниями, но мы рассмотрим ещё две: (Слайд №6)
Дизъюнкция – логическая операция, которая двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Для записи дизъюнкции используются следующие знаки: ИЛИ, ˅, |, +.
Дизъюнкцию можно описать в виде таблицы истинности: (см. справочный материал)
| А | В | A˅B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Дизъюнкцию ещё называют логическим сложением.
(Слайд №7)
Инверсия – логическая операция, которая высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Для записи инверсии используются следующие знаки: НЕ, ,¬.
| А | В | ¬A | ¬В |
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 | |
Инверсию ещё называют логическим отрицанием.
Назовите логическое значение инверсии для высказывания В.
При построении таблиц истинности есть определенная последовательность действий. Давайте запишем: (Слайд №8)
1. Определить количество строк в таблице:
-
количество строк = 2n+1, где n – количество логических переменных.
2. Определить количество столбцов в таблице:
-
количество столбцов = количеству логических переменных + количество логических операций.
3. Построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов (¬, &, V);
-
приоритеты: ( ), ¬, &, V.
4. Заполнить столбцы входных переменных наборами значений.
5. Заполнить таблицу истинности, выполняя логические операции в соответствии с приоритетами действий.
Возьмем для примера логическую формулу: ¬(A&B)
и построим таблицу истинности для этого составного высказывания.
Количество строк: 22+1=5, количество столбцов: 2+2=4. Далее заполняем варианты исходных высказываний А В. Теперь заполняем другие столбцы по порядку логических операций.
| А | В | A&B | ¬( A&B) |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 |
-
Закрепление изученного материала
Разберем следующее упражнение вместе. (Слайд №10) и работа на доске и в тетради.
Учебник: стр. 39 №8 (1, 3)
-
В&(АVВ)
Количество логических переменных: 2. Логических операций: 2.
Значит, строк в таблице 22+1=5, столбцов 2+2=4.
| A | B | AVB | В&(АVВ) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
3) А&(A˅B˅C)
Количество логических переменных: 3. Логических операций: 3
Значит, строк в таблице 23+1=9, столбцов 3+3=6.
| А | В | С | A˅B | (A˅B)˅C | А&((A˅B)˅C) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Задание для самостоятельной работы на готовых карточках.(Слайд №11)
Вам надо заполнить таблицы истинности по столбцам
, выполняя логические операции в соответствии с установленной последовательностью.
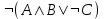
| А | В | С | | | | 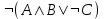 |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
Ответ: (Слайд №12)
| А | В | С | 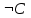 | 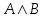 | 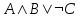 |  |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 |
-
Обобщение урока, домашнее задание (2 мин). (Слайд №12)
На этом уроке мы изучили понятие «таблицы истинности», познакомились с алгоритмом построения таблиц истинности, а также научились строить их для составных логических выражений, не вникая в смысл самого высказывания.
Д/З: учебник п.1.3.2, 1.3.3 стр. 24-30, №8(2, 4), стр. 39. Задание выполнить в тетради по аналогии с рассмотренными сегодня таблицами.
Прошу вас оценить урок, заполнив карточки.
Приложение 2
Выпишите пары соответствий в первом и втором столбцах:
| 1. Логика | 1. ИСТИНА и ЛОЖЬ |
| 2. Высказывание | 2. Наука о формах и способах мышления |
| 3. Алгебра логики | 3. Наука об операциях над высказываниями |
| 4. Значение логической переменной | 4. А |
| 5. Логическая переменная | 5. Повествовательное предложение, содержание которого однозначно может быть истинным или ложным |
1______, 2_______, 3______, 4_______, 5________.
Выполнил__________________________________________
Приложение 3
Задание для самостоятельной работы: Постройте таблицу истинности логического выражения

| А | В | С | | | |  |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |