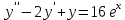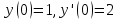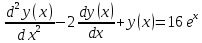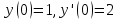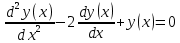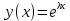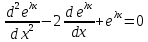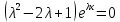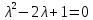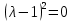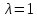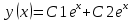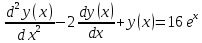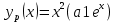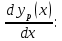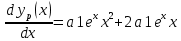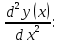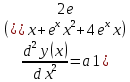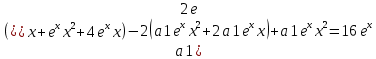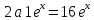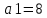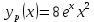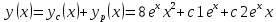Файл: Дифференциальное и интегральное исчисления функции одной переменной.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 43
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение
высшего образования
«Северный (Арктический) федеральный университет имени М.В. Ломоносова»
| Высшая школа энергетики, нефти и газа |
(наименование высшей школы / филиала / института / колледжа)
КОНТРОЛЬНАЯ РАБОТА
| По дисциплине/междисциплинарному курсу/модулю | Высшая математика | |
| | ||
| | ||
| На тему | Дифференциальное и интегральное исчисления функции одной переменной. | |
| Дифференциальные уравнения. | ||
| | ||
| | | ||||
| | | ||||
| | | ||||
| | | ||||
| | | ||||
| | | ||||
| | Руководитель: Попов Василий Николаевич | ||||
| | (Ф.И.О. руководителя, должность / уч. степень / звание) | ||||
| Отметка о зачете | | | | | |
| | | (отметка прописью) | | (дата) | |
| Руководитель | | | | В.Н.Попов | |
| | | (подпись руководителя) | | (инициалы, фамилия) | |
Архангельск 2022
Вариант 9
Задание 1
Найти производные
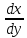 данных функций.
данных функций.а)
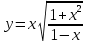 , б)
, б) 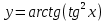 , в)
, в) 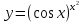
Решение:
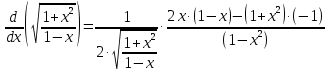
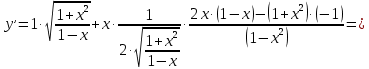
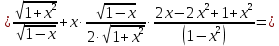
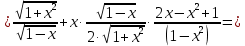
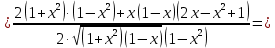
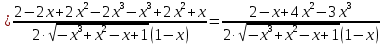
б)
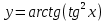 ,
,Решение:
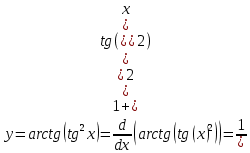
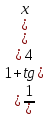
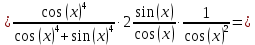
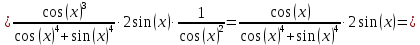
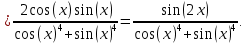
в)
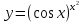
Решение:
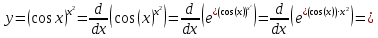
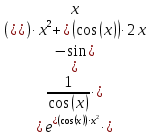
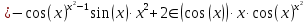
Задание 2
Исследовать методами дифференциального исчисления функцию и построить ее график, используя результаты исследования.
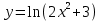
Решение
-
Найдем область определения функции.
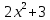 ,
, 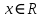 .
.-
Исследуем функцию на четность – нечетность
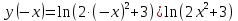 ,
,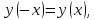 значит функция четная
значит функция четная
, а ее график симметричен относительно оси ординат.
-
Исследуем функцию на периодичность.
Данная функция не является периодической.
-
Найдем точки пересечения с осями координат.
Нет пересечения с осью Х.
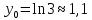 .
.-
Найдем экстремумы и интервалы монотонности функции.
Найдем производную заданной функции:
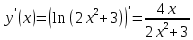
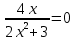
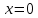




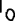
В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 - точка минимума.
-
Найдем интервалы выпуклости и вогнутости и точки перегиба.
Найдем вторую производную заданной функции:
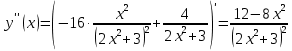 .
.Находим корни уравнения.
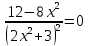
Находим точки перегиба:
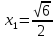
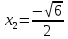
Функция выпукла
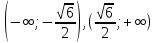 .
.Функция вогнута
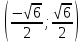
-
Найдем асимптоты
Исследуем поведение функции вблизи точек разрыва
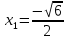 ,
, 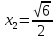 .
.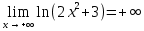 .
.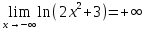 .
.Таким образом, нет горизонтальных асимптот.
Найдем наклонную асимптоту.
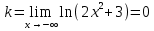
Таким образом, наклонных асимптот нет.
8. График функции изображен на рисунке 1.
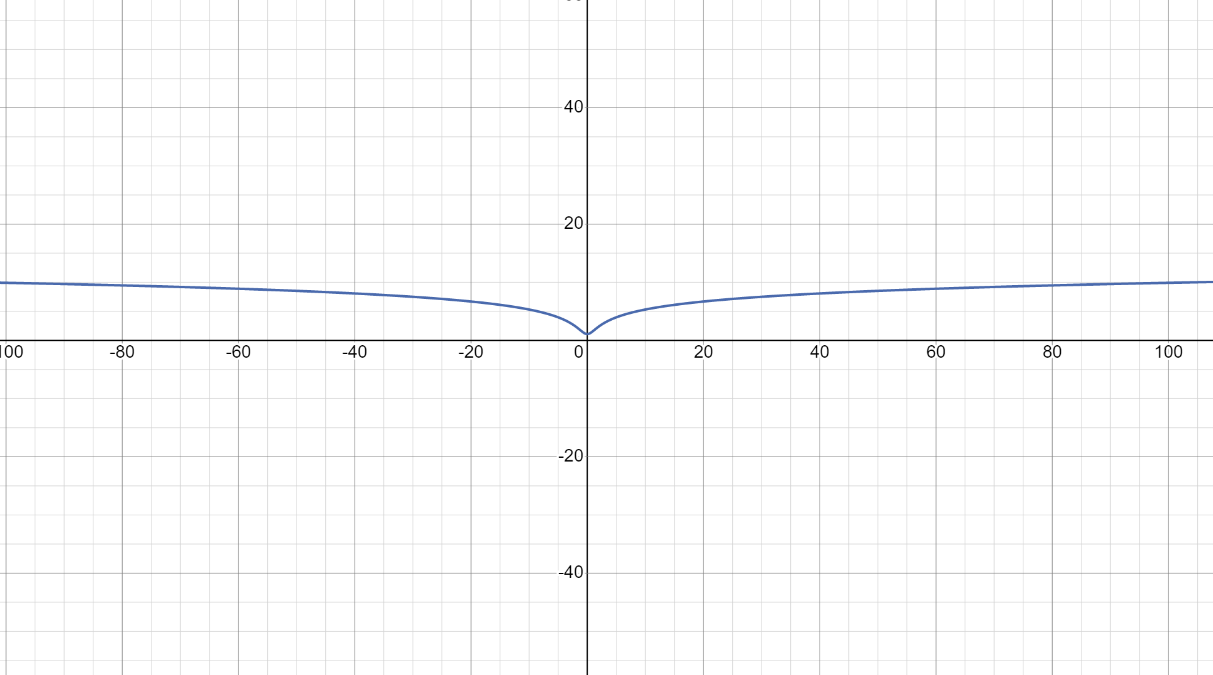
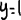
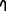
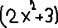
Задание 3
Найдите неопределенные интегралы. В п. а) и б) результаты проверить дифференцированием.
а)
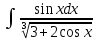 , б)
, б) 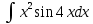 , в)
, в) 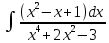 , г)
, г) 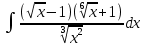
Решение:
а)
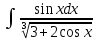
Используем подстановку
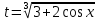 Следовательно, получим
Следовательно, получим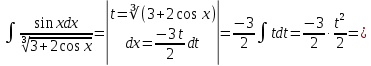
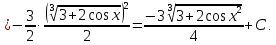
б)
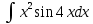
Используем подстановку
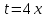 Следовательно, получим
Следовательно, получим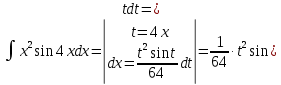
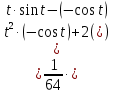
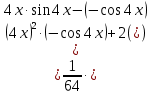
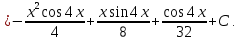
в)
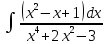
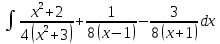
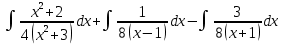
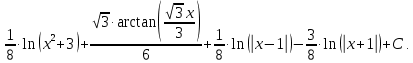
г)
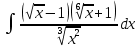
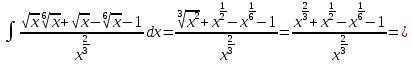
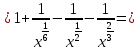
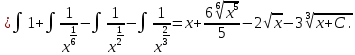
Задание 4
Вычислите определенные интегралы.
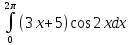
Решение:
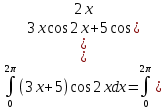
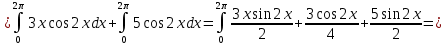
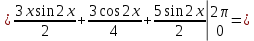
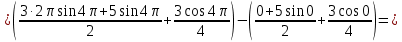
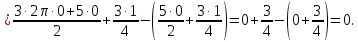
Задание 5
Найдите общее решение дифференциального уравнения.
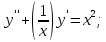
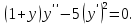
Решение:
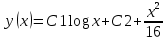
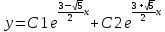
Задание 6
Решите задачу Коши