Добавлен: 06.12.2023
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант №3
Задача №1
Два точеных заряда
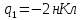 и
и 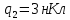 находятся на расстоянии
находятся на расстоянии 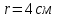 друг от друга. Найти напряженность и потенциал электростатического поля в точке, удаленной от первого заряда на расстояние
друг от друга. Найти напряженность и потенциал электростатического поля в точке, удаленной от первого заряда на расстояние 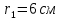 и от второго на
и от второго на 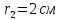 .
.Д
 ано: Решение
ано: Решение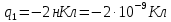
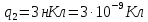
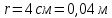
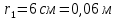
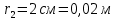
Найти:
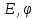
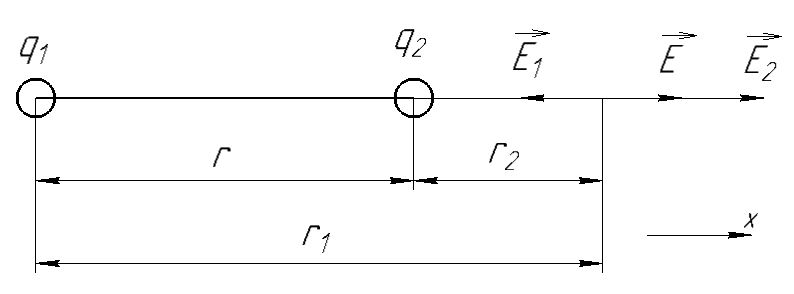
Из анализа числовых значений расстояний
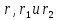 получим, что оба заряда и искомая точка лежат на одной прямой (см. рисунок). По определению суммарная напряженность в искомой точке будет равна векторной сумме напряженностей от первого и второго зарядов:
получим, что оба заряда и искомая точка лежат на одной прямой (см. рисунок). По определению суммарная напряженность в искомой точке будет равна векторной сумме напряженностей от первого и второго зарядов: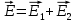
В проекции на ось Ох (см. рисунок) получим,
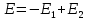
Найдем напряженности, создаваемые в искомой точке первым и вторым зарядами в отдельности. Напряженность, создаваемая точечным зарядом, определяется по формуле:
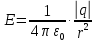
где
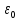 – диэлектрическая постоянная;
– диэлектрическая постоянная;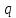 – величина точечного заряда;
– величина точечного заряда;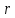 – расстояние от заряда до искомой точки.
– расстояние от заряда до искомой точки.
1-й заряд
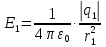
2-й заряд
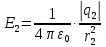
В итоге получим,
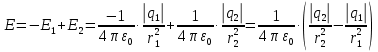
Суммарный потенциал, создаваемый в некоторой точке системой зарядов, определяется как алгебраическая сумма потенциалов, создаваемых в искомой точке каждым из зарядов в отдельности.
В данном случае получим,
Потенциал, создаваемый точечным зарядом, определяется по формуле:
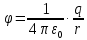
где
 – диэлектрическая постоянная;
– диэлектрическая постоянная; – величина точечного заряда;
– величина точечного заряда; – расстояние от заряда до искомой точки.
– расстояние от заряда до искомой точки.Тогда,
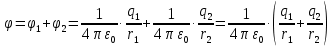
Подставим в полученные формулы числовые значения:
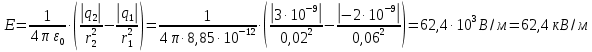
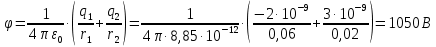
Ответ:
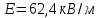 ,
, 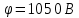 .
.Задача №2
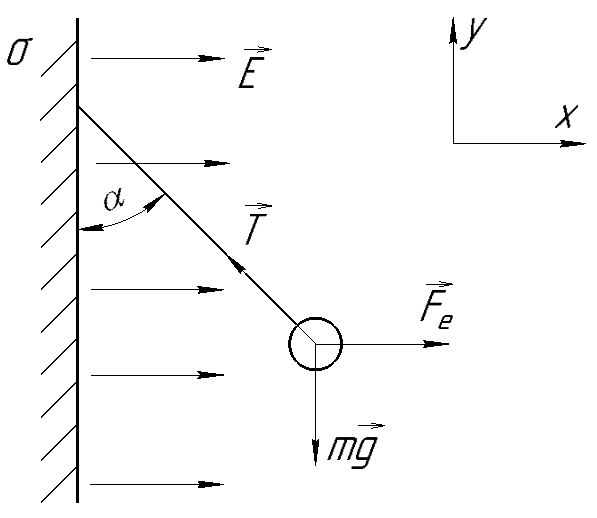
К бесконечно протяженной плоскости (поверхностная плотность заряда
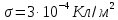 ) прикреплена нить, на которой висит шарик (масса
) прикреплена нить, на которой висит шарик (масса 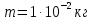 , заряд
, заряд 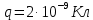 ), заряженный одноименно с плоскостью. Нить с шариком отклонена на угол
), заряженный одноименно с плоскостью. Нить с шариком отклонена на угол  . Определить угол отклонения нити
. Определить угол отклонения нити  .
.Д
 ано: Решение
ано: Решение 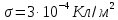
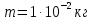
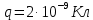
Найти:

На заряженный шарик действуют сила тяжести
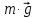 , сила натяжения нити
, сила натяжения нити 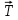 и сила
и сила 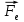 со стороны электрического поля, создаваемого заряженной плоскостью. Запишем для шарика второй закон Ньютона:
со стороны электрического поля, создаваемого заряженной плоскостью. Запишем для шарика второй закон Ньютона: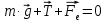
В проекции на оси Ох и Оу (см. рис.) получим:
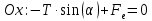
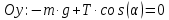
В итоге получим следующую систему уравнений.
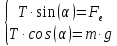
Разделим первое уравнение системы на второе:
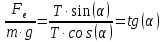
Сила, действующая со стороны электрического поля на электрический заряд, определяется по формуле:
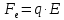
где
 – величина электрического заряда;
– величина электрического заряда;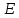 – напряженность электрического поля в точке, в которой расположен электрический заряд.
– напряженность электрического поля в точке, в которой расположен электрический заряд.Напряженность электрического поля, создаваемого бесконечной равномерно заряженной плоскостью, вычисляется по формуле:
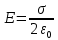
где
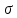 – поверхностная плотность заряда плоскости;
– поверхностная плотность заряда плоскости; – диэлектрическая постоянная.
– диэлектрическая постоянная.Подставим все полученные выше выражения в исходное.
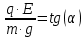
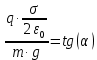
Выразим из полученного соотношения угол
 отклонения нити .
отклонения нити .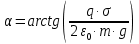
Подставим в полученную формулу числовые значения:
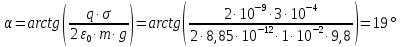
Ответ:
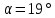 .
.Задача №3
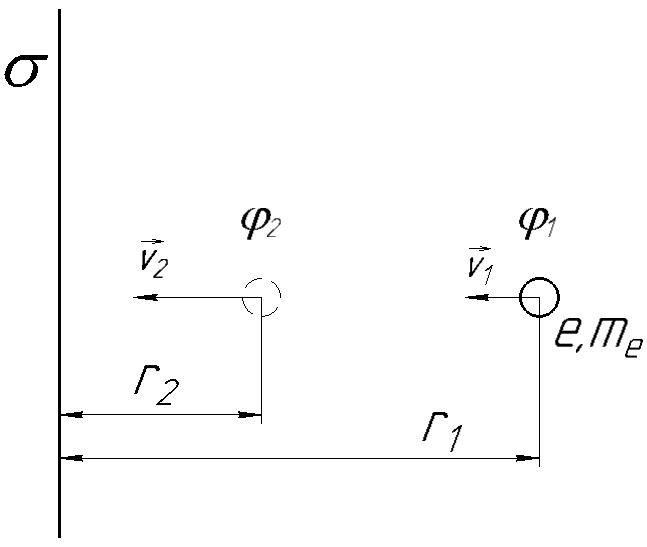
Электрическое поле образовано заряженной плоскостью, с поверхностной плотностью заряда
 . Электрон перемещается в поле от одной точки пространства (на расстоянии
. Электрон перемещается в поле от одной точки пространства (на расстоянии 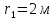 от плоскости) до другой (на расстоянии
от плоскости) до другой (на расстоянии 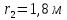 от плоскости), при этом ее скорость изменяется от
от плоскости), при этом ее скорость изменяется от 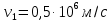 до
до 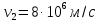 . Найти величину поверхностной плотности заряда
. Найти величину поверхностной плотности заряда  .
.Д
 ано: Решение
ано: Решение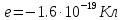
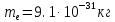
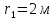
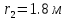
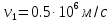
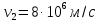
Найти:

Согласно закону сохранения энергии изменение кинетической энергии электрона равно работе сил электрического поля.
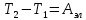
По определению работа сил, совершаемая при перемещении заряда в электрическом поле, вычисляется по формуле:
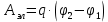
где
 – величина заряда;
– величина заряда;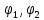 – потенциалы начальной и конечной точек, соответственно.
– потенциалы начальной и конечной точек, соответственно.Потенциал, создаваемый бесконечной равномерно заряженной плоскостью на расстоянии
 от плоскости, определяется по формуле:
от плоскости, определяется по формуле: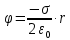
где
 – диэлектрическая постоянная;
– диэлектрическая постоянная; – поверхностная плотность заряда плоскости.
– поверхностная плотность заряда плоскости.По определению кинетическая энергия тела определяется по формуле:
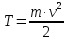
где
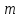 – масса тела;
– масса тела;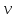 – скорость движения тела.
– скорость движения тела.Подставим все полученные выше формулы в исходную.
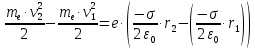
Выразим искомую величину поверхностной плотности заряда
 .
.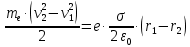
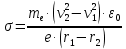
Подставим в полученную формулу числовые значения:
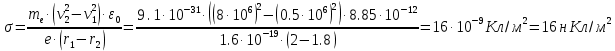
Ответ:
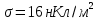 .
.Задача №4
Найти значение и направление тока через резистор
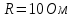 . Внутренние сопротивления бесконечно малы. Параметры цепи
. Внутренние сопротивления бесконечно малы. Параметры цепи 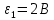 ,
, 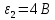 ,
, 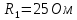 ,
, 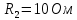 .
.Д
 ано: Решение
ано: Решение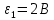
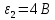
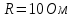
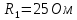
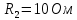
Найти:
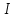
Для определения токов в ветвях цепи запишем первый и второй законы Кирхгофа.
Первый закон Кирхгофа (для правого узла схемы):