Добавлен: 06.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
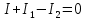
Второй закон Кирхгофа (для большого контура):
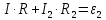
Второй закон Кирхгофа (для нижнего контура):
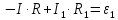
Получим итоговую систему трех уравнений:
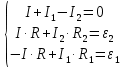
Решим данную систему относительно искомой силы тока
.
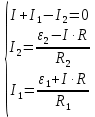
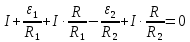
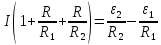
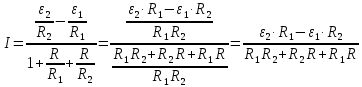
Подставим в полученную формулу числовые значения:
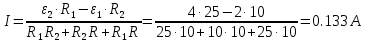
Поскольку вычисленное значение силы тока положительное, то направление силы тока соответствует направлению, указанному на рисунке.
Ответ:
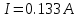.Задача №5
По двум прямолинейным бесконечно длинным проводникам текут токи
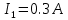и 
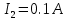в одном направлении. Проводники параллельны друг другу и расстояние между ними 
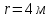. Найти значение вектора магнитной индукции в точке, находящейся на расстоянии 
от первого проводника и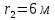 
от второго.Дано: Решение
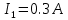
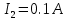
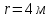
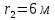
Найти:
По условию указано, что требуется найти величину вектора магнитной индукции в точке, удаленной на расстоянии
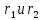от первого и второго проводников соответственно. Следовательно, на указанных трех точках (если рассматривать плоскость, перпендикулярную проводникам) можно построить треугольник со сторонами 
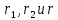. Для указанных по условию расстояний неравенство треугольника – длина любой стороны треугольника всегда меньше или равна сумме длин двух его других сторон – вырождается в равенство.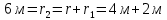
Следовательно, треугольник вырождается в прямую линию. На рисунке представлена схема для данных условий.
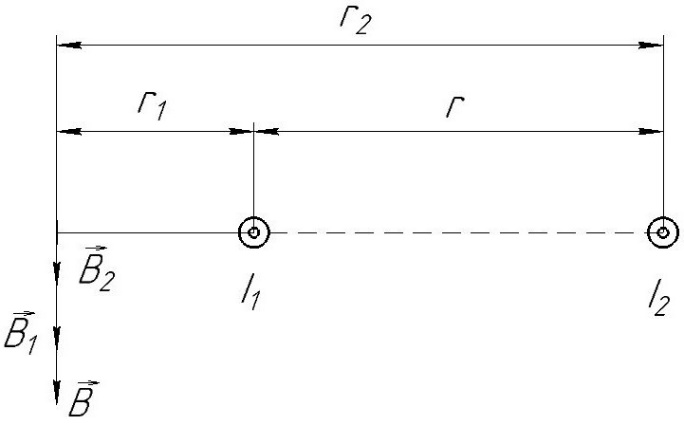
Согласно принципу суперпозиции, суммарная индукция в искомой точке будет равна векторной сумме магнитных индукций, создаваемых в данной точке первым и вторым проводниками с током.
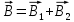
Длинный прямой проводник с током создает вокруг себя круговое магнитное поле. Величина индукции поля в некоторой точке, удаленной от проводника на расстояние
, определяется по формуле: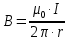
где
– величина тока в проводнике; – расстояние до точки, в которой определяется магнитная индукция;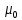
– магнитная постоянная.Тогда получим,
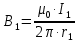
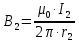
В данном случае вектора магнитных индукций первого и второго проводника сонаправлены (см. рис). Тогда величина вектора суммарной магнитной индукции будет равна:
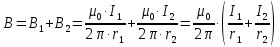
Подставим в полученную формулу числовые значения:
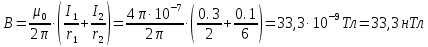
Ответ:
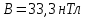.Задача №6
Электрон влетает в плоский горизонтальный конденсатор параллельно его пластинам со скоростью
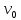. Длина конденсатора 
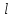. Напряженность электрического поля конденсатора 
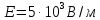. При вылете из конденсатора электрон попадает в магнитное поле с индукцией 
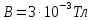, перпендикулярное электрическому и параллельное начальной скорости влета электрона в конденсатор. Электрон в магнитном поле начинает двигаться по винтовой линии радиусом 
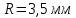и шагом 
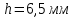. Определить 
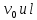.Дано: Решение
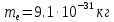
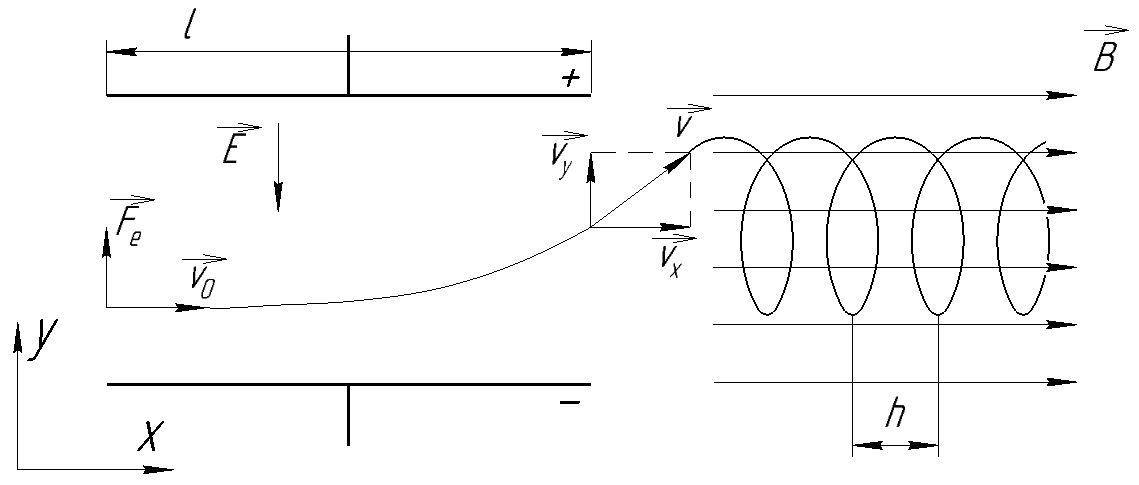
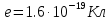
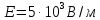
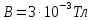
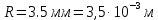
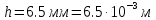
Найти:
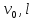
При пролете через конденсатор на электрон действует сила Кулона, которая отклоняет электрон от первоначального направления.
Запишем второй закон Ньютона:
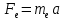
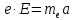
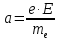
где
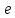– электрический заряд электрона;
– напряженность электрического поля в конденсаторе;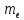
– масса электрона.В начальный момент времени электрон имел только продольную составляющую скорости (вдоль оси
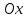). Следовательно, движение электрона вдоль оси
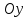– равноускоренное движение без начальной скорости. Тогда скорость электрона можно рассчитать по формуле: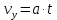
где
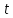– время пролета электрона через конденсатор;Время пролета электрона через конденсатор равно:
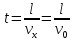
Тогда,
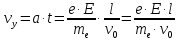
На электрон, движущийся в магнитном поле, действует сила Лоренца
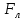, которая придает электрону центростремительное ускорение 
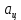. Запишем для электрона второй закон Ньютона: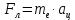
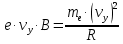
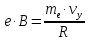
Тогда радиус винтовой линии будет равен.
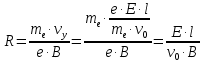
Период обращения электрона по винтовой линии равен:
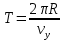
С другой стороны, за один период электрон проходит вдоль оси
расстояние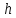 
:
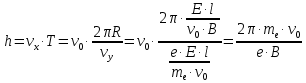
Выразим из полученных выше соотношений искомые величины начальной скорости электрона
и длины конденсатора 
.
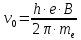
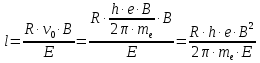
Подставим в полученные формулы числовые значения:
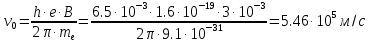
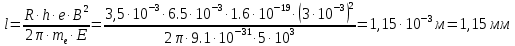
Ответ:
, 
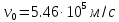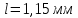.Задача №7
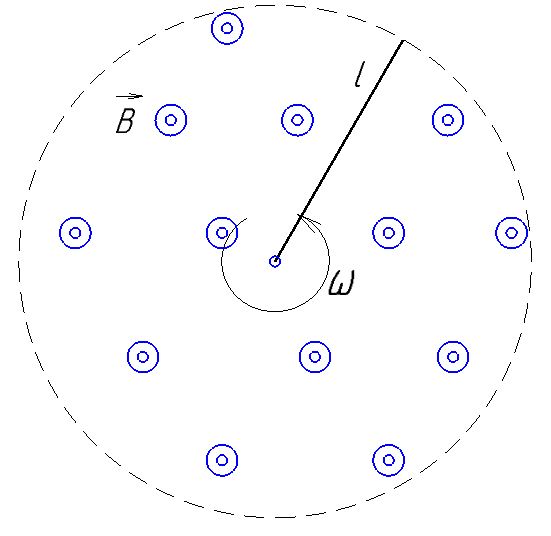
В магнитном поле, индукция которого
, вращается стержень длиной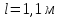 
с угловой скоростью 
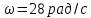. Ось вращения проходит через конец стержня и параллельна магнитному полю. При этом на концах стержня возникает ЭДС индукции 
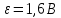. Найти индукцию магнитного поля .Д
ано: Решение
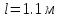
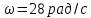
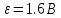
Найти:
Запишем закон электромагнитной индукции Фарадея:
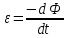
где
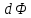– изменение магнитного потока через контур.В данном случае за один оборот стержень пересекает магнитный поток, равный:
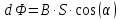
где
– величина индукции магнитного поля;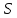
– площадь контура;
– угол между вектором индукции и нормалью к плоскости контура.В данном случае площадь контура – площадь круга, радиуса, равного длине стержня
:
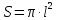
По условию указано, что плоскость вращения перпендикулярна силовым линиям поля. Тогда,
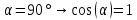
Поскольку рассчитывается изменение магнитного потока для одного оборота, то промежуток времени равен периоду вращения:
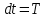
Угловая скорость вращения связана с периодом вращения соотношением: