65.5-45,5=20 млн. руб. абсолютный прирост за 2014год

65-45,5=19.5млн. руб. абсолютный прирост за 2015год

72-45,5=26,5 млн. руб. абсолютный прирост за 2016год

100-45,5=54,5 млн. руб. абсолютный прирост за 2017год

Темпы роста базисные и цепные

50/45,5*100=109,9% темп роста цепной 2013год

65.5/50*100=131 темп роста цепной за 2014год

65,5/65*100=100,76 темп роста цепной за 2015год

72/65*100= 110,7%темп роста цепной за 2016год

100/72*100=138,8% темп роста цепной за 2017год

50/45,5*100=109,9% темп роста базисный 2013год

65.5/45,5*100=143,95% темп роста базисный за 2014год

65/45,5*100=143,95% темп роста базисный за 2015год

72/45,5*100= 158,24%темп роста базисный за 2016год

100/45,5*100=219,78% темп роста базисный за 2017год

Темпы прироста цепные и базисные

4,5/50*100=9% темп прироста цепной в 2013 года к 2012года.

15.5/65,5*100=23,66% темп прироста цепной 2014 года к 2013года.

0,5/65*100=0,76% темп прироста цепной 2015 года к 2014года.

7/72*100=9,72% темп прироста цепной 2016 года к 2015года.

28/100*100=28% темп прироста цепной 2017 года к 2016года.

4,5/45*100=10% темп прироста базисный 2013 к 2012года.

20/45,5*100=43,95% темп прироста базисный 2014 к 2012года

19,5/45,5*100=42,85% темп прироста базисный 2015 к 2012года

26,5 /45,5*100= 58,24% темп прироста базисный 2016 к 2012года

54,5 /45,5*100=119,78% темп прироста базисный 2017 к 2012года.

(45,5+50+65)/3=53,5 млн.₽ скользящей средней с 2012-2014годы

(65+72+100)/3=79 млн.₽ скользящей средней с 2015-2017годы

(45,5+50+65,5+65+72+100)/5=79,6 млн.₽ средний уровень ряда

Задача 2.5.

Имеются данные по двум предприятиям (табл. 2.5)

Таблица 2.5

Предприятия	Базисный год		Отчетный год
	выработано продукции	отработано чел. – дней, тыс. ед.	выработано продукции, тыс. т.	отработано чел. – дней, тыс. ед.
№ 1 № 2	15000 2700	130 70	17000 2500	150 60
всего	17700	200	19500	210

Определить индексы динамики производительности труда по каждому предприятию и в целом по двум предприятиям переменного и фиксированного состава; индекс влияния структурных сдвигов на изменение среднего уровня производительности труда.

---

Решение

17000-15000/15000=0,13 индексы динамики производительности труда 1 предприятия

2500-2700/2700=-0,07 индексы динамики производительности труда 2 предприятия
15000/130=115,38 тыс.тон чел индексы динамики производительности труда по 1 предприятию за базисный год

17000/150=113,33 тыс.тон чел индексы динамики производительности труда по 1 предприятию за отчетный год

2700/70=38,57 тыс.тон чел индексы динамики производительности труда по 2 предприятию за базисный год.

2500/60=41,66 тыс.тон чел индексы динамики производительности труда по 2 предприятию за отчетный год.

19500/17700=1,1 Индекс производительности труда переменного состава.

19500/(17700*210/210)=1,1 Индекс производительности труда фиксированного состава

(17700*210/210)/(17700*200/200)=1 индекс влияния структурных сдвигов на изменение среднего уровня производительности труда
Задача 2.6.

Определите коэффициент корреляции на основе следующих данных о рабочем стаже и выполнении сменных норм выработки рабочими производственного участка.

Таблица 2.6

Стаж работы, лет	1	2	3	4	5	6	7	8	9	10
Среднее выполнение норм, %	97	100	101	104	106	108	110	112	115	118

Проанализируйте результаты.

Решение

Уравнение линейной регрессии с y на x имеет вид:

Уравнение линейной регрессии с x на y имеет вид:

Найдем необходимые числовые характеристики.
Выборочные средние:

x= (97*1 + 100*1 + 101*1 + 104*1 + 106*1 + 108*1 + 110*1 + 112*1 + 115*1 + 118*1)/10 = 107.1

y= (1*1 + 2*1 + 3*1 + 4*1 + 5*1 + 6*1 + 7*1 + 8*1 + 9*1 + 10*1)/10 = 5.5
Дисперсии:
σ²_x = (97²*1 + 100²

---

*1 + 101²*1 + 104²*1 + 106²*1 + 108²*1 + 110²*1 + 112²*1 + 115²*1 + 118²*1)/10 - 107.1² = 41.49
σ²_y = (1²*1 + 2²*1 + 3²*1 + 4²*1 + 5²*1 + 6²*1 + 7²*1 + 8²*1 + 9²*1 + 10²*1)/10 - 5.5² = 8.25
Откуда получаем среднеквадратические отклонения:
σ_x = 6.441 и σ_y = 2.872
и ковариация:
Cov(x,y) = (97*1*1 + 100*2*1 + 101*3*1 + 104*4*1 + 106*5*1 + 108*6*1 + 110*7*1 + 112*8*1 + 115*9*1 + 118*10*1)/10 - 107.1*5.5 = 18.45
Определим коэффициент корреляции:


Запишем уравнения линий регрессии y(x):

и вычисляя, получаем:
y_x = 0.44 x - 42.13
Запишем уравнения линий регрессии x(y):

и вычисляя, получаем:
x_y = 2.24 y + 94.8
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (107.1; 5.5) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.

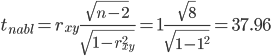
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10-m-1 = 8 находим t_крит:
t_крит (n-m-1;α/2) = (8;0.025) = 2.752
где m = 1 - количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - знаÑ

---

Смотрите также файлы

• Литература Практическое задание 2 слушатель Харалампова Ольга Владимировна Преподаватель.doc

• Лицо привлечено к уголовной ответственности за незаконную предпринимательскую деятельность при сдаче в аренду жилого помещения третьим лицам без регистрации в качестве индивидуального предпринимателя.docx

• Тематика курсовых проектов (работ).docx

• Классного руководства можно фантазировать вечно. Говорят, ничто не ценится так дешево, и не дается так дорого как Классное руководство.docx

• Супруги Платоновы нуждались в денежных средствах для завершения строительства загородного коттеджа.docx