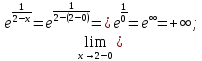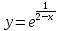
Вариант 10Задание 3. Провести полное исследование функций и построить их графики:б) Порядок исследования (согласно схеме исследования из тетради):

1. 
   Область определения и область значения
   

1. 
   Область определения:
   

2. 
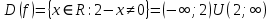
   Область значения: обычно не определяется в начале исследования, т.к. требуется нахождение асимптот и локальных экстремум с помощью первой производной. В разбираемом тобой примере я этого не нашёл. Но если требуется в начале, то для данной функции:
   
3. 
   E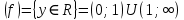
   

Рекомендую опустить данный пункт или написать в конце исследования после графика, т.к. после построения графика область значений будет видна на графике

2. 
   Точки разрыва, асимптоты
   

1. 
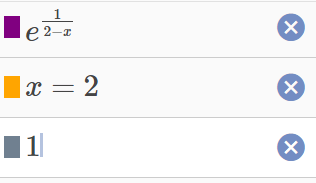
   Точки разрыва: x = 2
   
   1. 
      
      

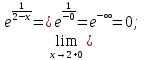
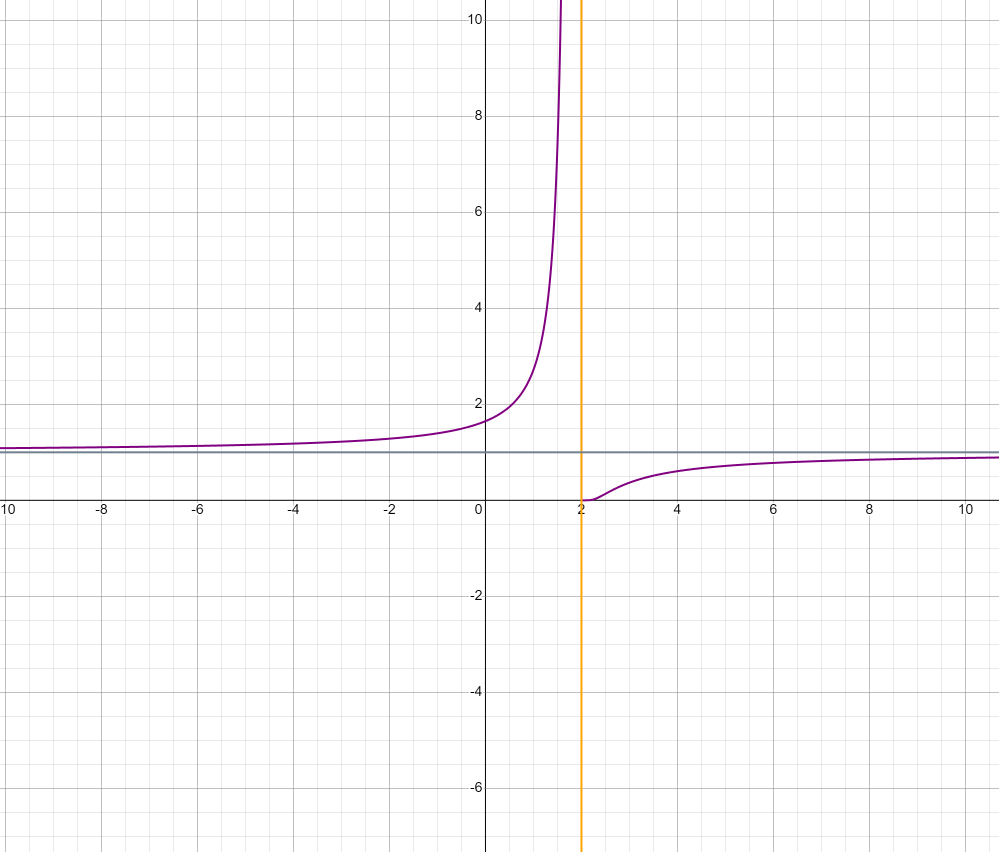
Точка x = 2 – разрыв II рода. Прямая x = 2 – вертикальная асимптота.

2. 
    
   

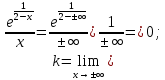
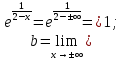
Отсюда прямая y = 1 – горизонтальная асимптота.

3. 
   Точки пересечения с осями координат
   

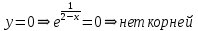
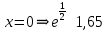
3.1. С ОХ: Нет корней, следовательно, нет точек пересечения с ОХ.3.2. С ОY: Точка пересечения с ОY имеет координаты (0;1,65)

4. 
   Чётность и периодичность
   

4.1. Чет/нечет:

---

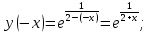
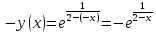
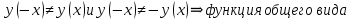
4.2. ПериодичностьФункция не является периодической. (Нет такого периода Т, чтобы для любого x выполнялось: F(x + T) = F(x)). Либо как у тебя в тетради, почерк не разобрал.

5. 
   Исследование с помощью первой производной
   

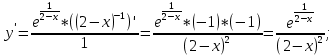
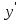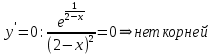
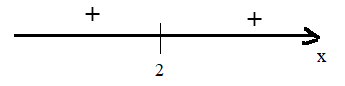
– не существует в т. х = 2 (Точка разрыва).Пояснение к рисунку: знак минус - функция убывает, знак плюс – функция возрастает.Функция не имеет критических точек.

6. 
   Исследование с помощью второй производной
   

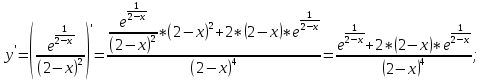
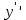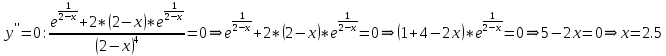
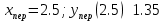
– не существует в т. х = 2 (Точки разрыва).Точка перегиба: (2.5; 1.35)

7. 
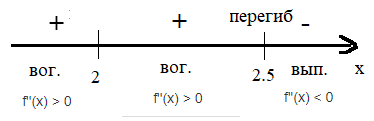
   Доп. точки – пункт для того, чтобы построить график в тетради. (по аналогии с вар10(а))
   

На графике отметь точку перегиба.

8. 
   Построение графика
   

---

Смотрите также файлы

• Особенности рассмотрения дел.docx

• Производственной практики пм. 03 Оказание доврачебной медицинской помощи при неотложных и экстремальных состояниях для специальности 34. 02. 01. Сестринское дело.docx

• День театра. Томский театр живых кукол 2Ку.docx

• 4тосан 2. Роботтар мен киборгтер лемі блімі бойынша жиынты баалау.docx

• Рабочая программа по биологии по программе основного общего образования, адаптированной для детей с нарушением интеллекта, для учащегося 8.docx