Файл: Решение Находим частную производную по аргументу х, считая, что у const (постоянная).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 51
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
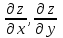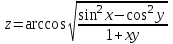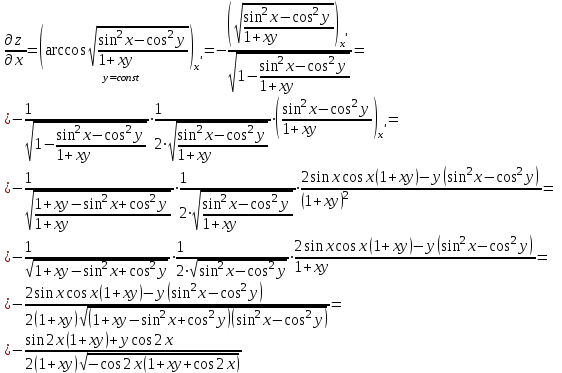
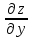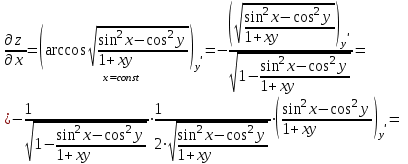
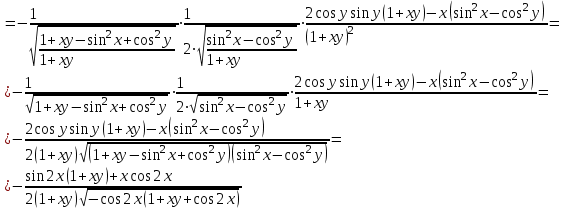
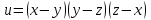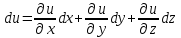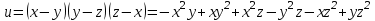
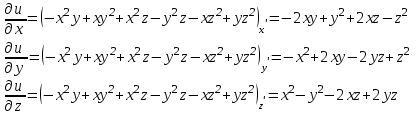
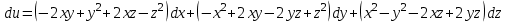
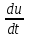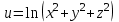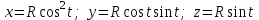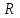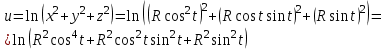
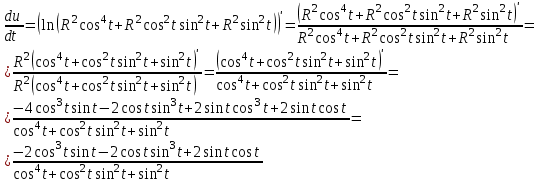
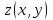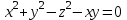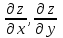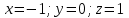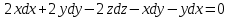
Задание 1.Найти частные производные функции .Решение:Находим частную производную по аргументу х, считая, что у = const (постоянная):Аналогично находим , считая, что х = const : Задание 2.Найти полный дифференциал функции .Решение:Полный дифференциал .Задание 3.Найти производную , если , где , ( – параметр).Решение:Задание 4.Функция задана уравнением . 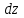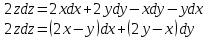Найти при .Решение:Дифференцируем обе части: Находим отсюда выражение для : 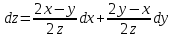– полный дифференциал 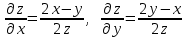– частные производные В точке
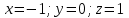
получим: 
.
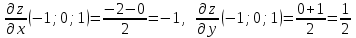Задание 5.
Составить уравнения касательной плоскости и нормали к поверхности 
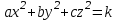в точке 
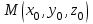на ней.
Решение:
1) Касательная плоскость к поверхности 
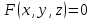в точке 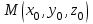представляется уравнением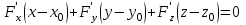
Тут 
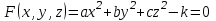
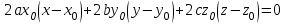, сократим на 2: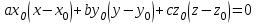
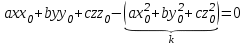
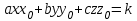– касательная плоскость.
2) Нормаль к поверхности 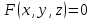в точке 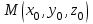представляется уравнением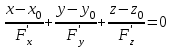
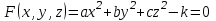
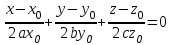, сократим на 1/2:
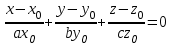– нормаль.