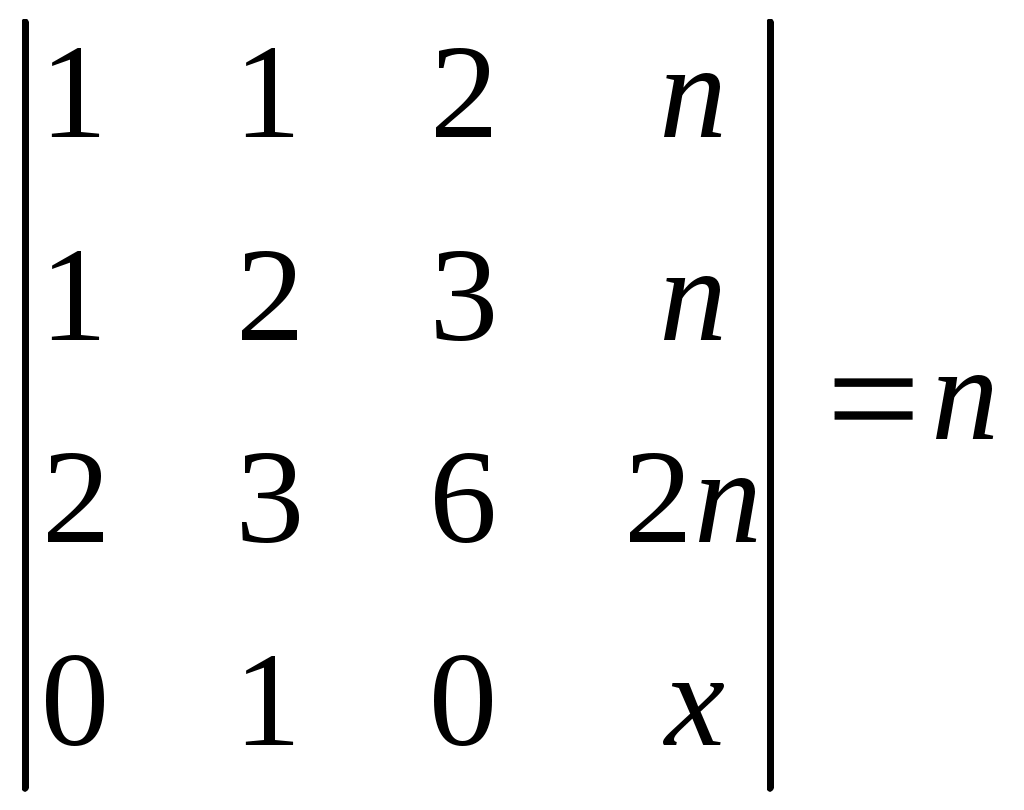
Контрольная работапо математикеВариант 3Задача 1. Решите уравнение: РешениеПрименим метод алгебраических дополнений. Получим нули в столбце 1. Из строки 2 вычтем почленно строку 1:

1	2	3	n
1	1	2	n
0	1	1	0

Затем из строки 3 вычтем строку 1, предварительно умножив строку 1 на 2.

2	3	6	2n
2	2	4	2n
0	1	2	0

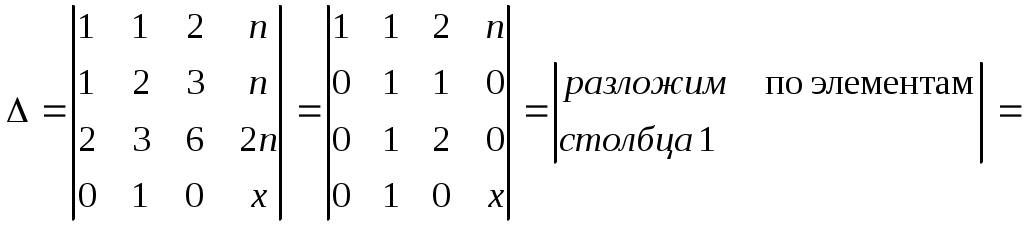
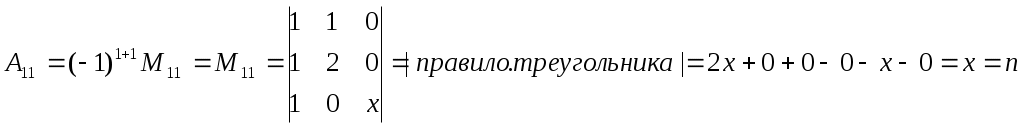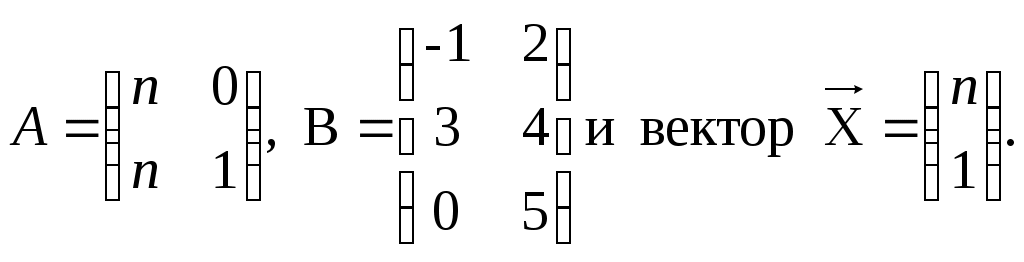
Строку 4 перепишем, так как в ней есть 0.В результате получим определитель, равный исходному:=Вычислив алгебраическое дополнение А₁₁:=3Ответ: х=3Задача 2. Даны матрицы Найдите: ВА, АХ, ХА, А^-1, А^T , rangА, D=n(А^T)^Т – АЕ.Решение =

---

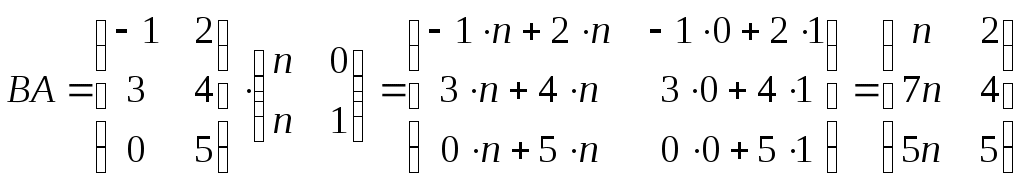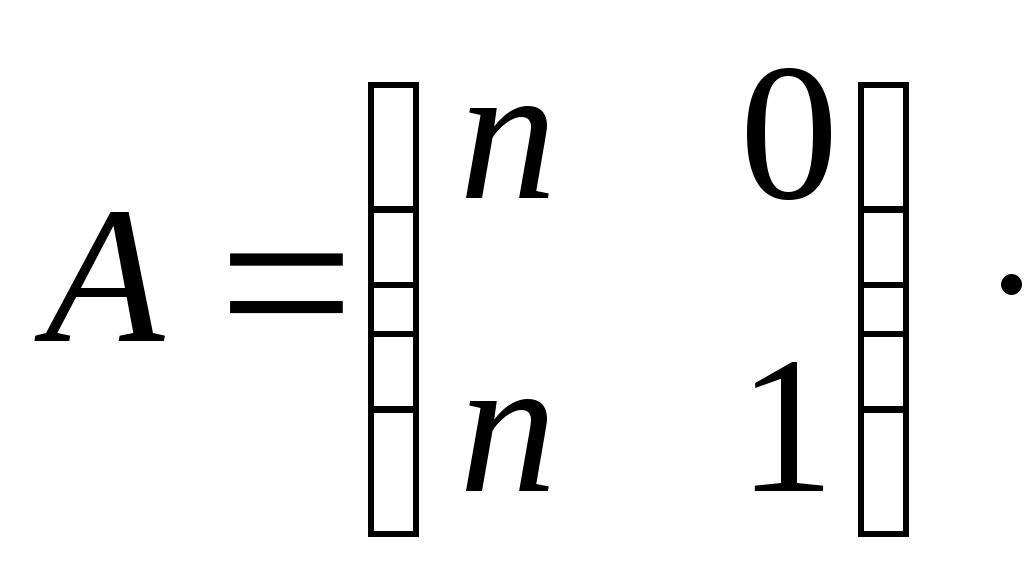
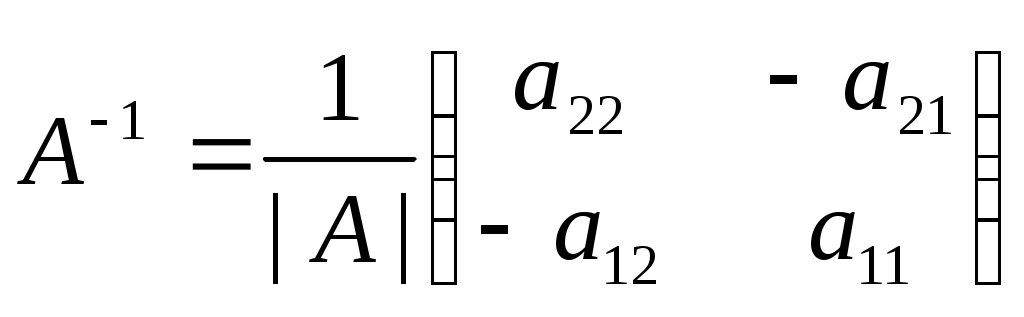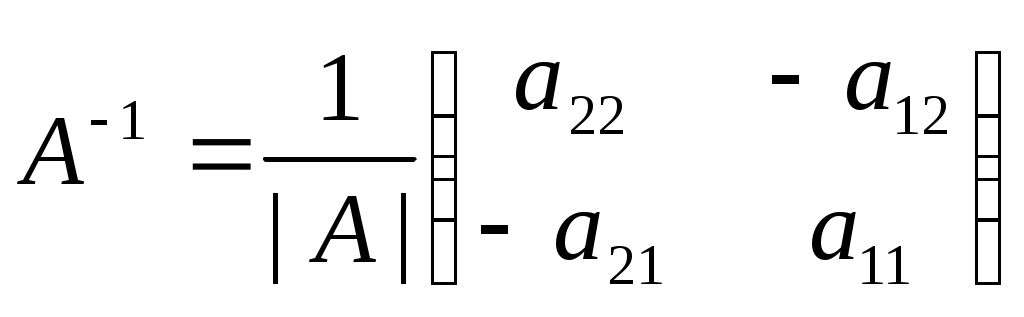
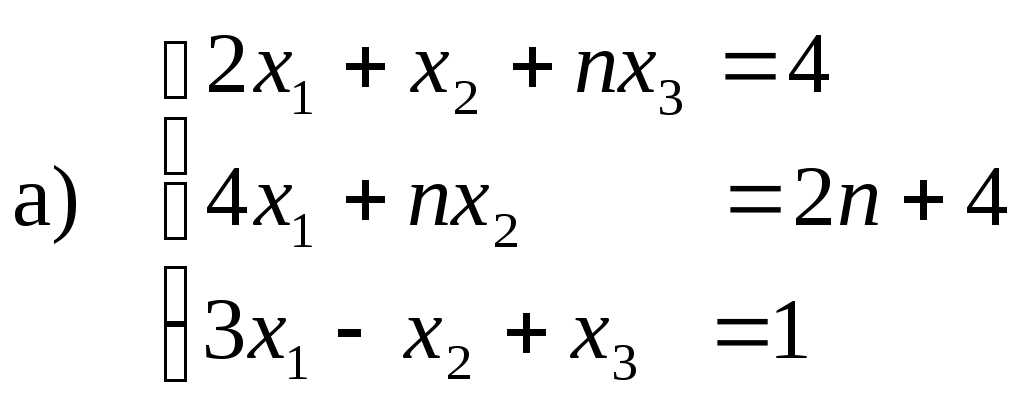
Произведение ХА не определено, так число столбцов в Х неравно числу строк А.Обратная матрица.Если , то Определитель матрицы =3.Тогда =Транспонирование матрицы: =Ранг А равен 2, так как Применим свойства матриц: D=n(А^T)^Т – АЕ= nА – А=(n-1)А ==(n-1) =2 =Задача 3. Исследуйте систему линейных уравнений с помощью определителей, решите методами Крамера, матричным, Гаусса.РешениеНайдем определитель системы: 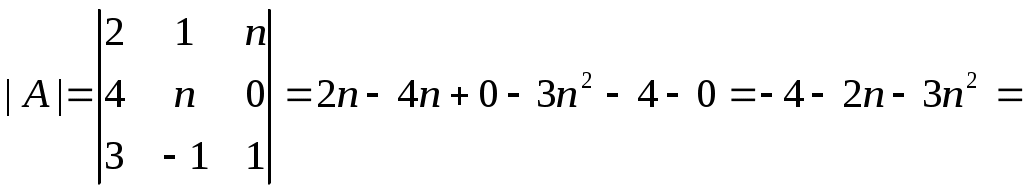-4-6-27= -370Система имеет единственное решение.1) Метод Крамера. 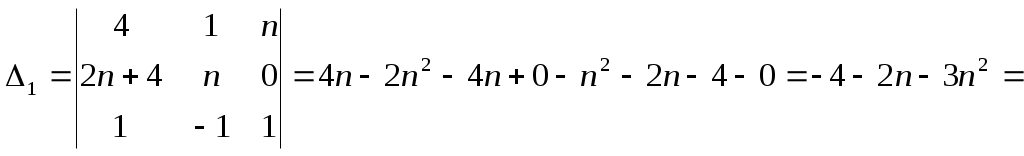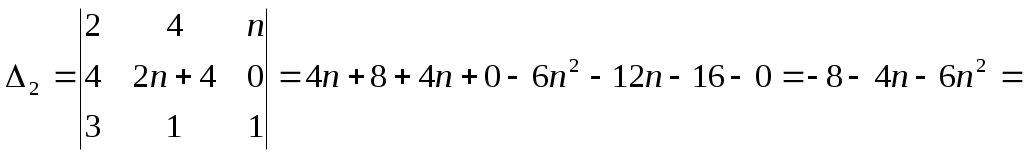,где Δ – определитель системы,Δ_{хj -} вспомогательные определители, каждый из которых получается из определителя Δ заменой столбца j столбцом свободных членов в_i.Найдем вспомогательные определители:-37-74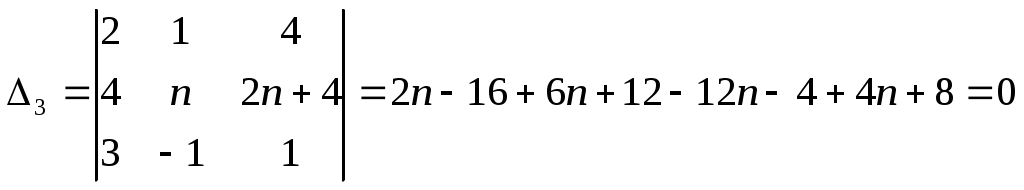Найдем значения неизвестных:

---

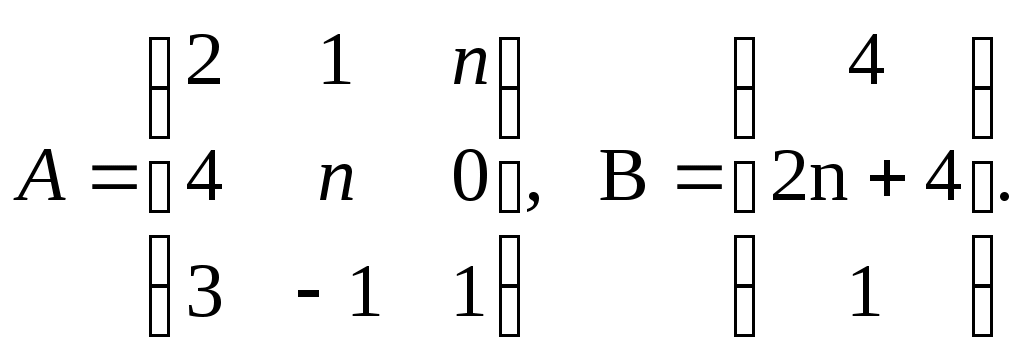
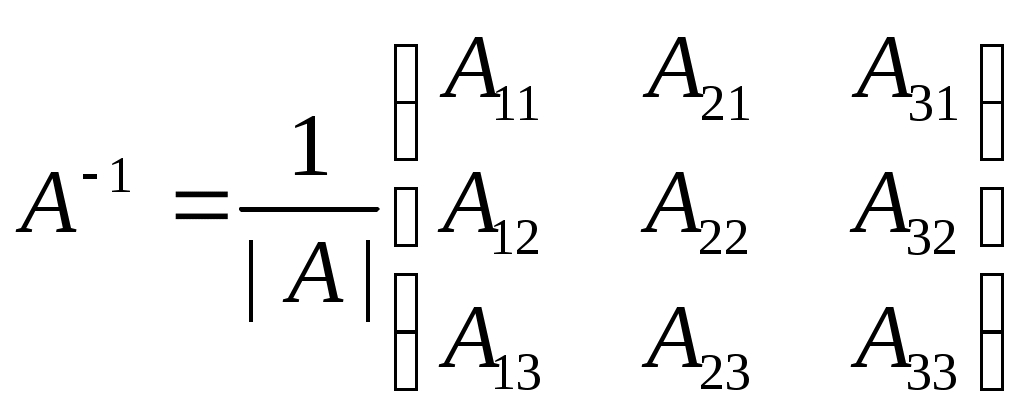
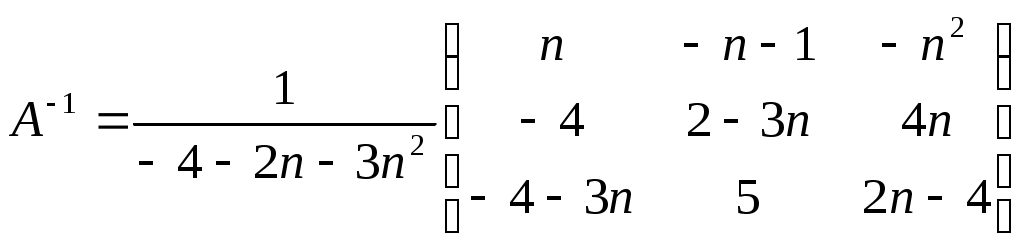
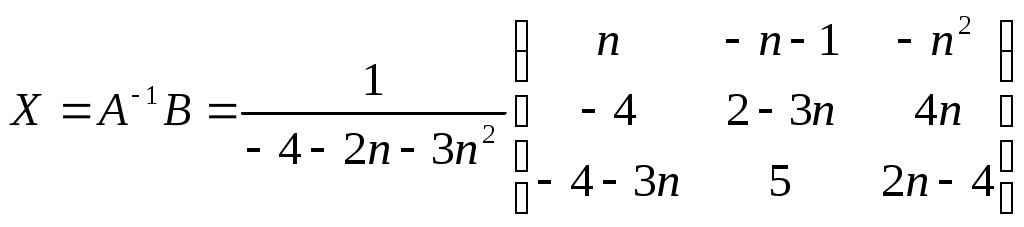
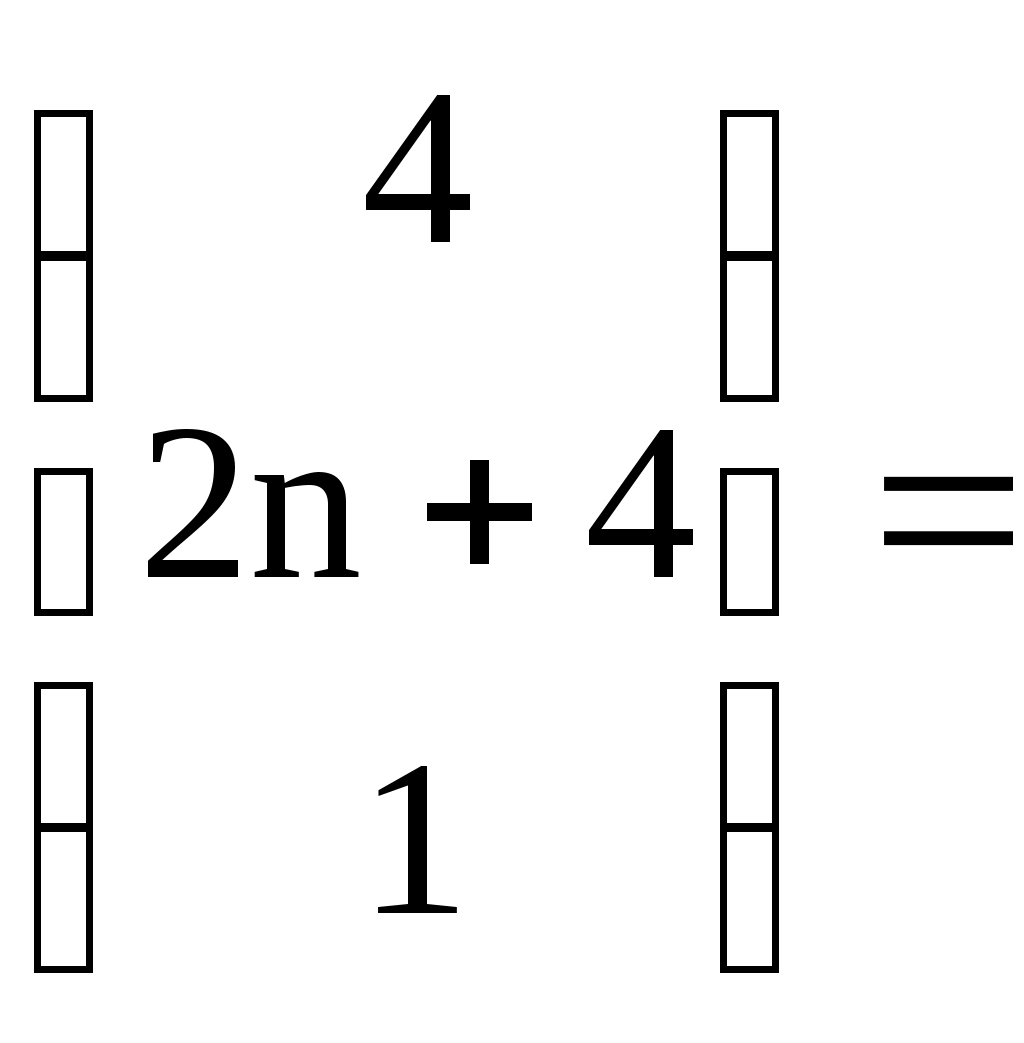
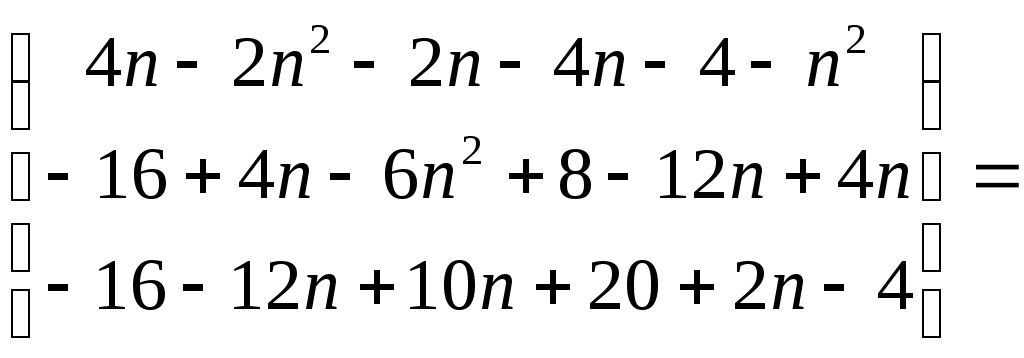
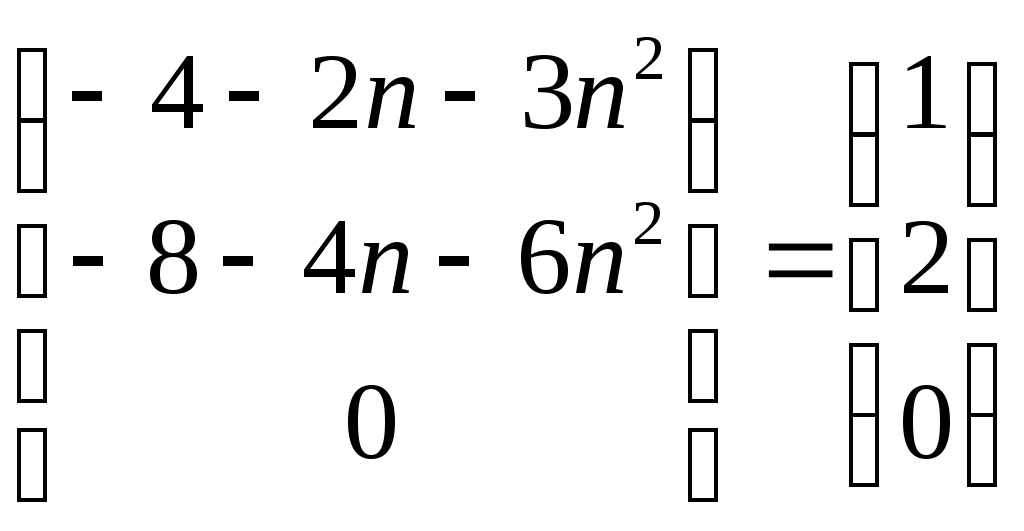
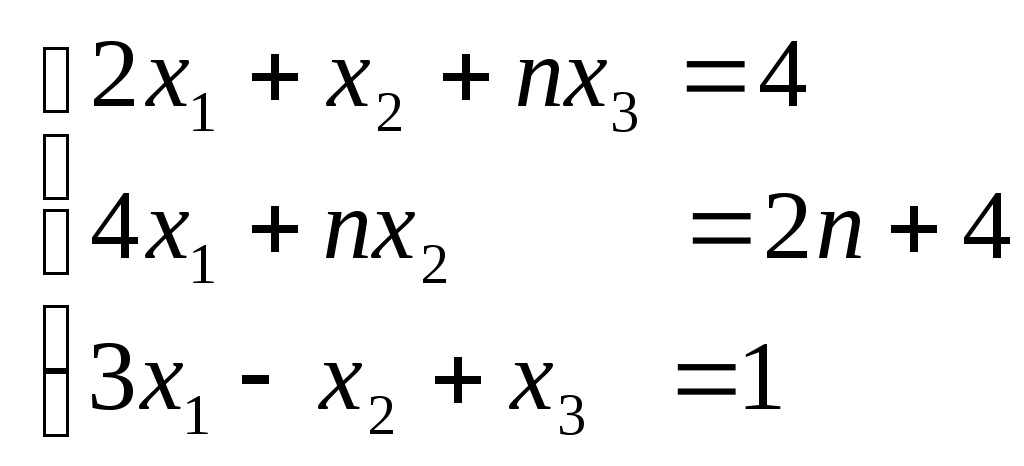
2) Матричный метод: X= А^-1В.Матрицы системы:Найдем обратную матрицу:Определитель системы: -37Найдем алгебраические дополнения: А_ij=(-1)^i+jM_ijА₁₁=(-1)¹⁺¹М₁₁=+М₁₁=А₂₁=(-1)²⁺¹М₂₁=-М₂₁= -Аналогично находим остальные дополнения.Получим: Найдем матрицу неизвестных: 3) Метод ГауссаПриведем систему с помощью элементарных преобразований к равносильной системе ступенчатого вида.Исключим неизвестную x₁Первое уравнение поделим на 2, получим: Из второго уравнения вычтем почленно новое первое уравнение, умноженное на 4:(n-2)x₂-2nx₃=2n-4Из третьего уравнения вычтем почленно новое первое уравнение, умноженное на 3:

---

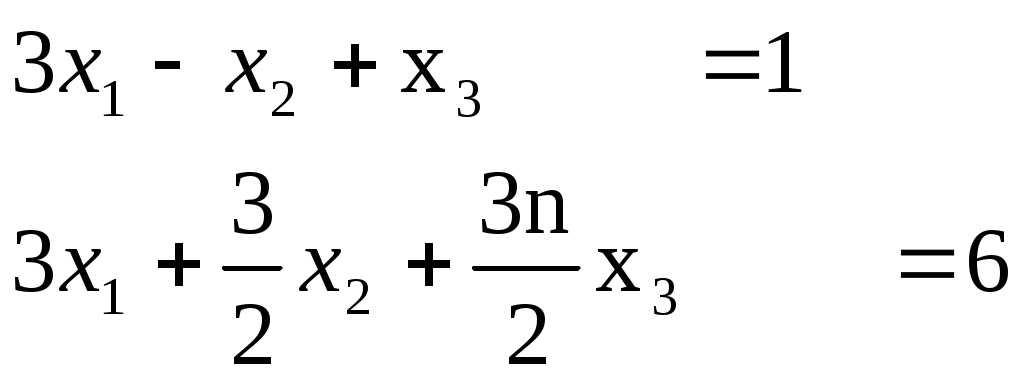
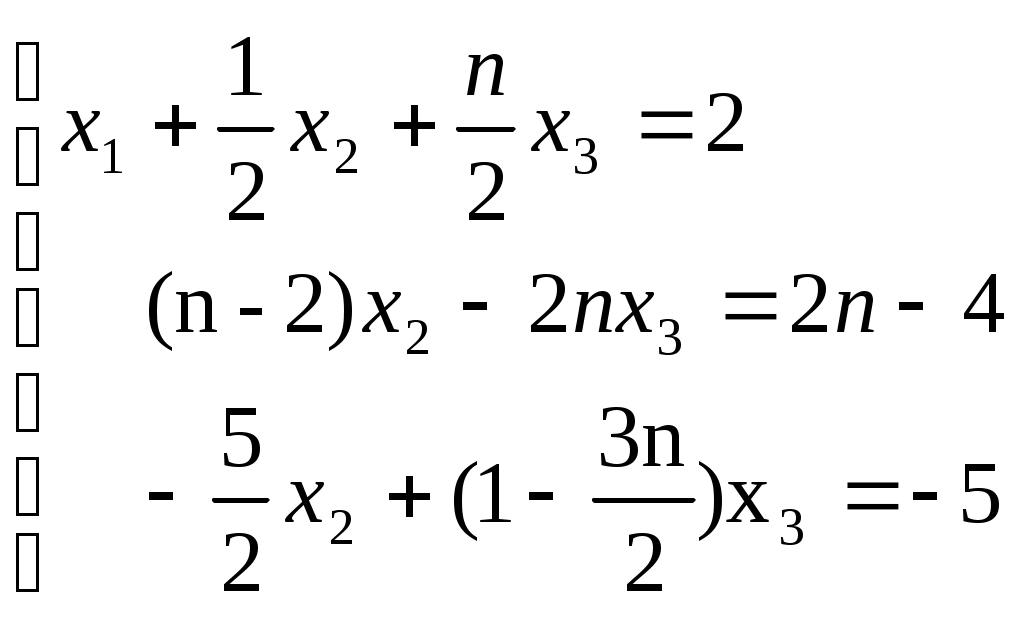
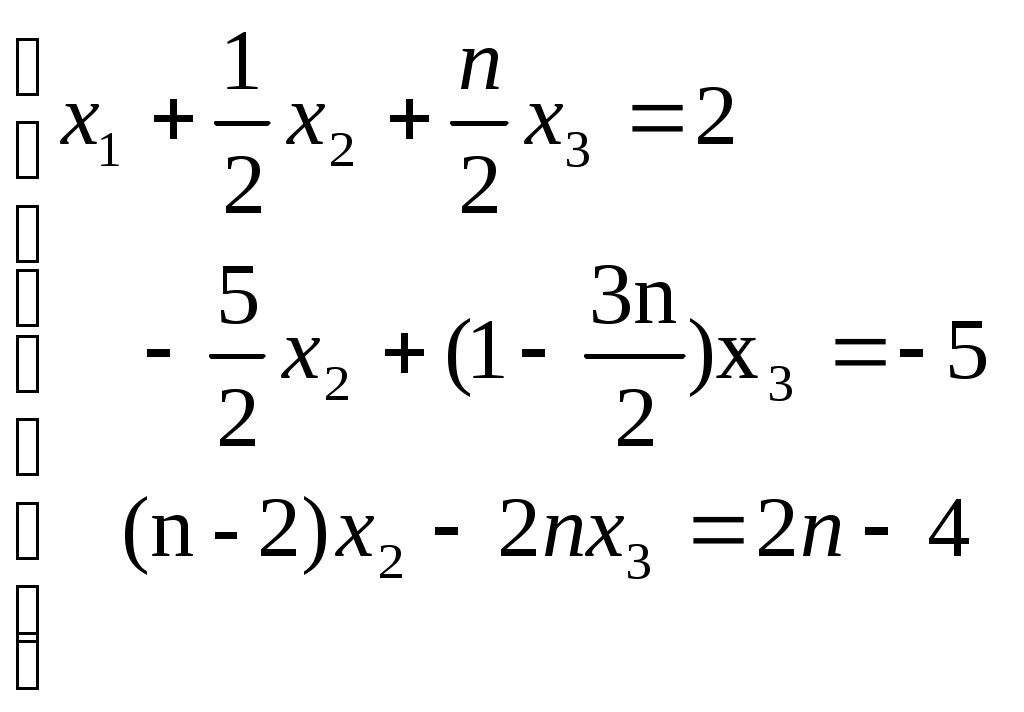
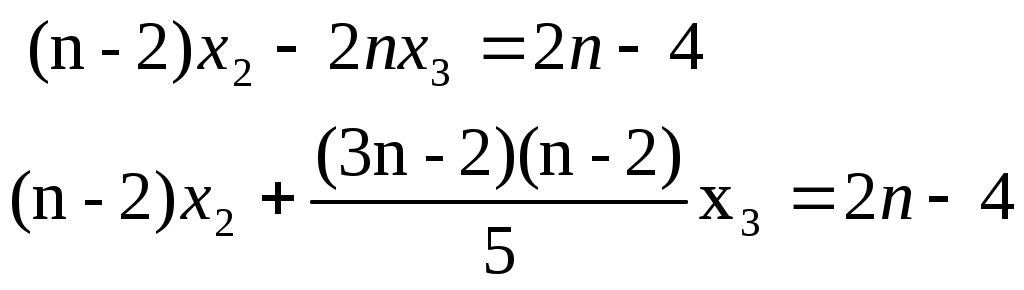
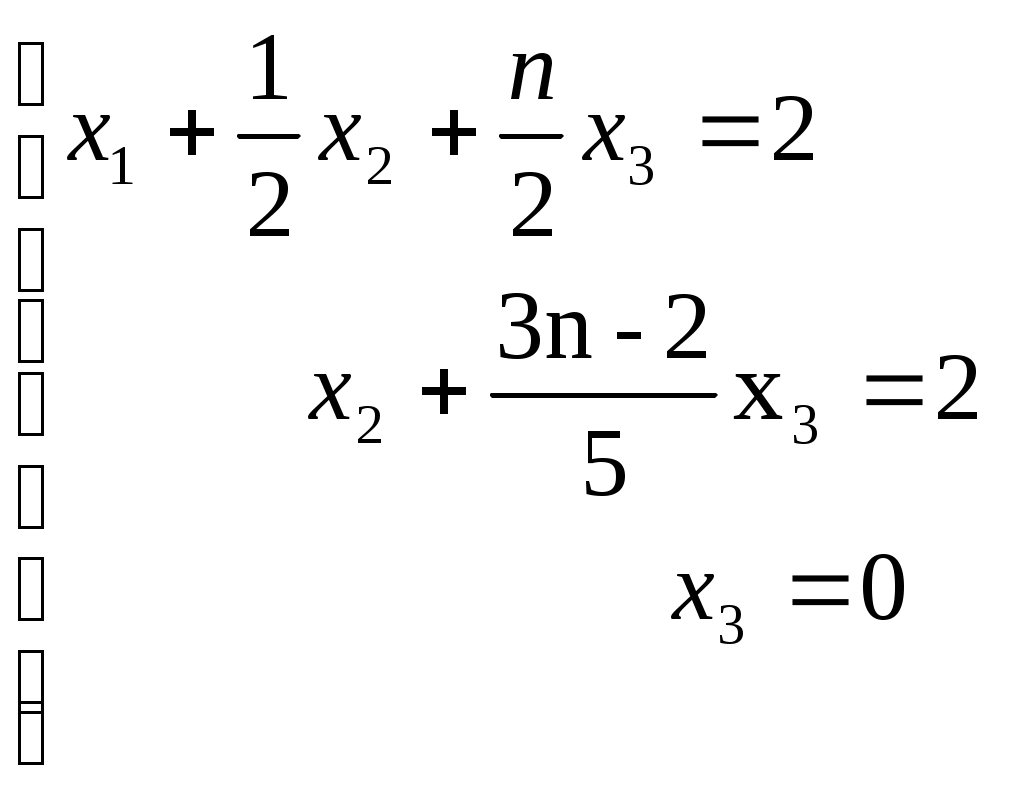
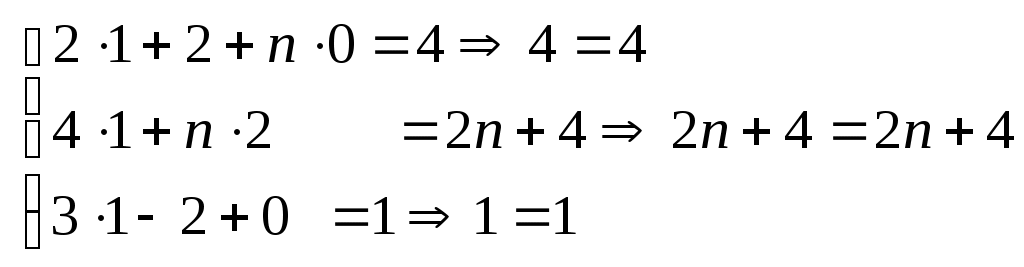
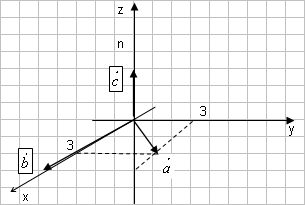
В результате получим равносильную систему:Исключим неизвестную x₂Поменяем местами второе и третье уравнения:Поделим второе уравнение на (-5/2): Из третьего уравнения вычтем второе, умноженное на (n-2):В результате получим равносильную систему:Из второго уравнения при x₃=0 получим x₂=2.Из первого уравнения:Проверка:Система решена правильноОтвет: х₁=1, х₂=2, х₃=0.Задача 4. Постройте векторы . 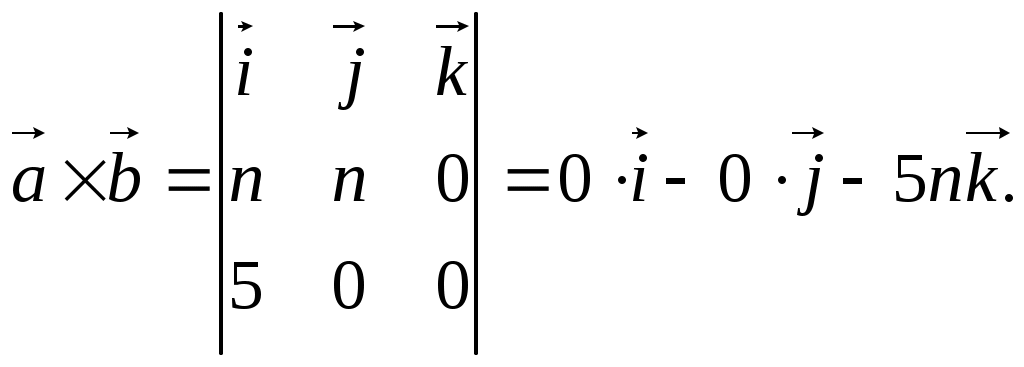Найдите:а) площадь треугольника, построенного на ,б) объем пирамиды, построенной на векторах .РешениеПостроим векторы.а) площадь треугольника, построенного на ,Используем геометрический векторного произведения: Модуль вектора =15Тогда 7,5.б) Объем пирамиды Используем геометрический смысл смешанного произведения:

---

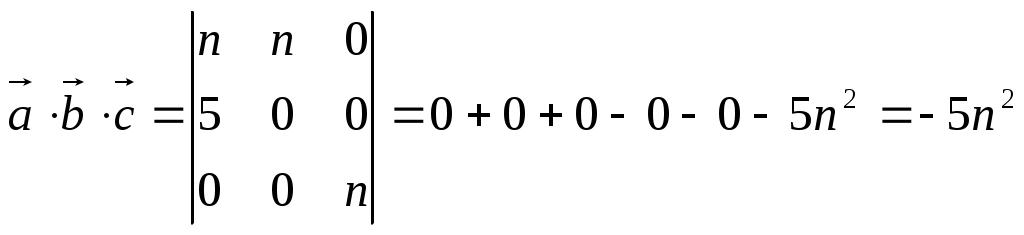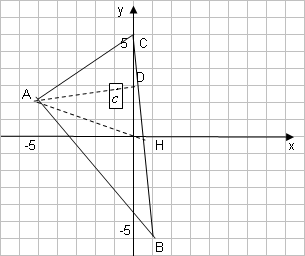
. Тогда =7,5Задача 5. Даны координаты вершин треугольника АВС: А(n-10,2), В(1,n-10), С(0,5) Сделайте чертеж. Найдите:1) длину и уравнение медианы АН; 2) длину и уравнение высоты AD.РешениеСделаем чертеж.1) Длина и уравнение медианы АНСначала найдем координаты точки М как середины отрезка ВС: M(0,5; -1)Подставляя координаты точек А и Мв уравнение:Получим: .Длина АМ:2) Длина и уравнение высоты ADПрямые АD и ВС перпендикулярны, поэтому их угловые коэффициенты . Уравнение ВС: Тогда:у-у_о=k(х-х_о) Задача 6. Даны координаты вершин пирамиды М₁М₂М₃М₄: М₁(2,0,0), М₂(0,-4,2), М₃(0,n,0), М₄(0,0,4). Сделайте чертеж. 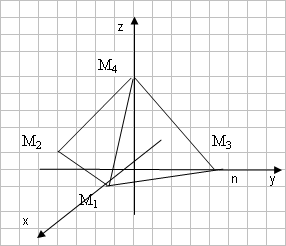Найдите:1) уравнение и длину ребра М₁М₂;2) угол между рёбрами М₁М₂ и М₁М₄;3) уравнение грани М₁М₂М₃;4) площадь грани М₁М₂М₃;5) объём пирамиды.РешениеСделаем чертеж.1) уравнение и длина ребра М₁М₂;Уравнения ребра М₁М₂ найдем как уравнения прямой, проходящей через две точки. Подставляя координаты точек в уравнения

---

Смотрите также файлы

• Факторы эволюции изоляция, изоляты и демы в популяциях человека.docx

• Бастауыш сынып оушыларыны каллиграфиялы машытарын жетілдіруде, сондайа жалпы кркем жазу жмысын жасартуда,сынып.docx

• Лабораторная работа по курсу общей физики "Изучение электростатического поля".docx

• Лауазымды міндеттер 4,5 класты станция бойынша кезекші.docx

• аза дебиеті.docx