Файл: Задача Решите уравнение Решение Применим метод алгебраических дополнений. Получим нули в столбце 1.doc
Добавлен: 06.12.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,
получим: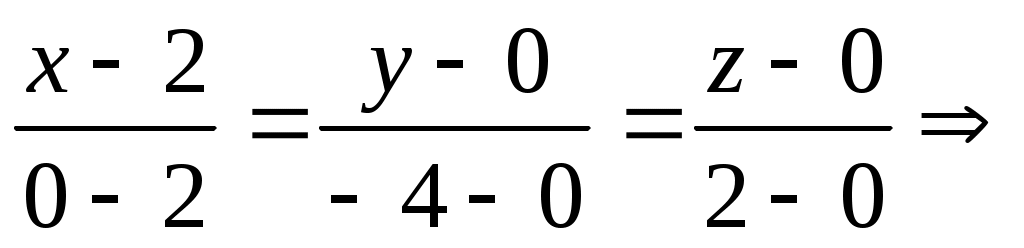
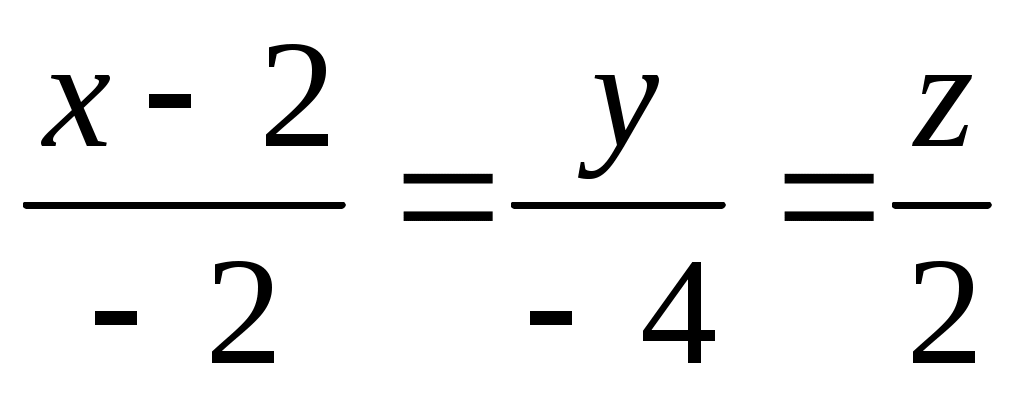 - канонические уравнения ребра М1М2.
- канонические уравнения ребра М1М2.
Длина ребра М1М2 равна расстоянию между точками М1и М2 или длине вектора: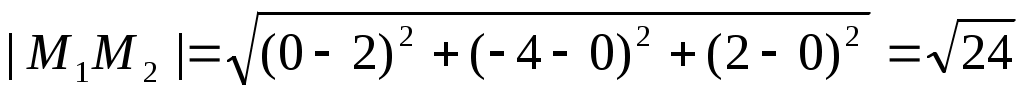 .
.
2) угол между рёбрами М1М2 и М1М4
Определим угол между сторонами М1М2 и М1М4 как угол между соответствующими векторами. Найдем координаты векторов:
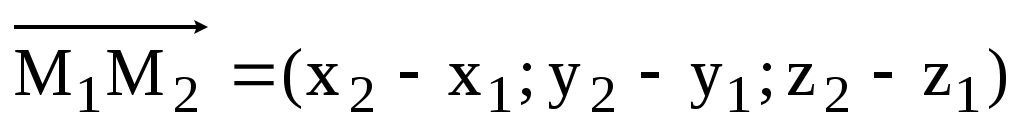 =
=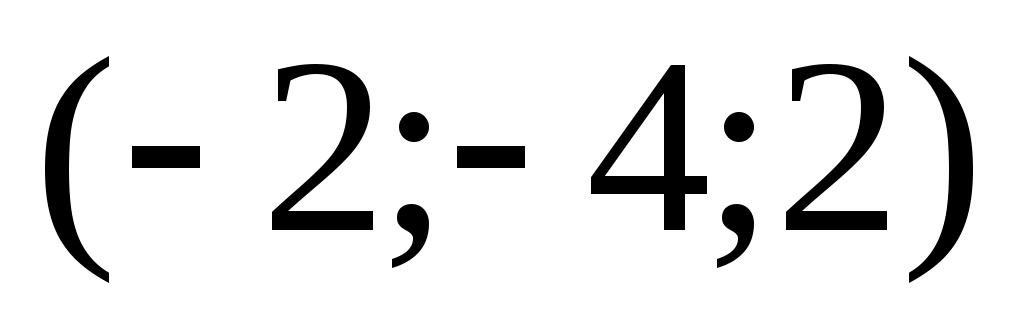 , длина вектора
, длина вектора 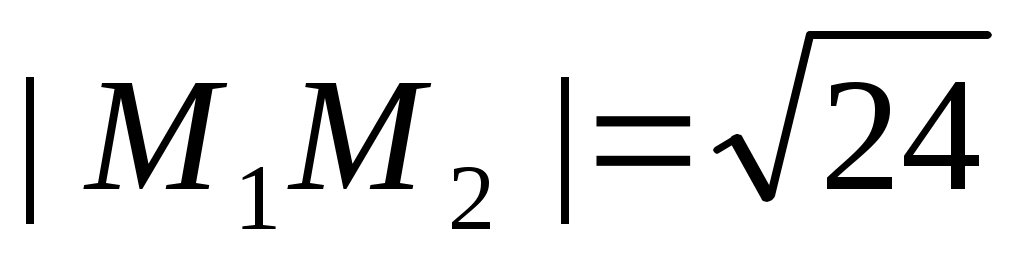
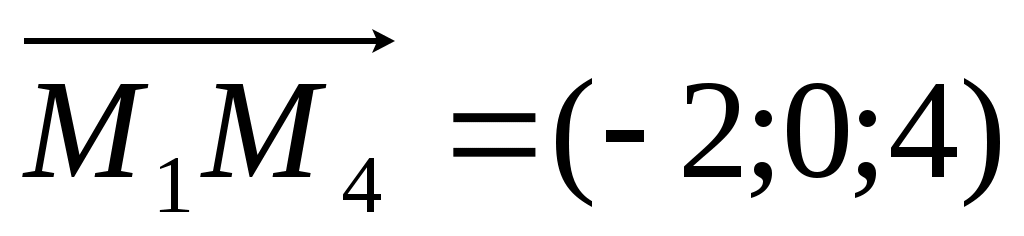 , длина вектора
, длина вектора 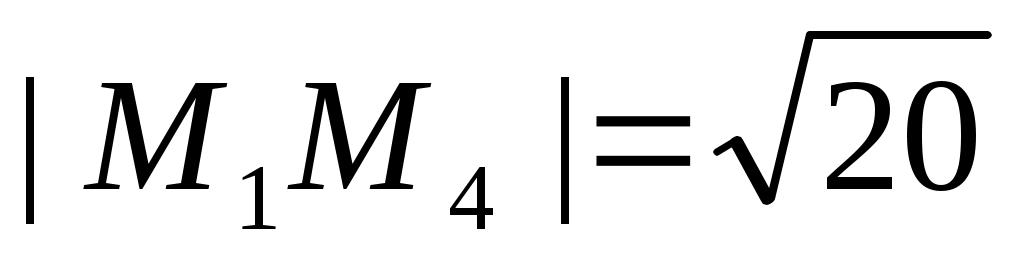
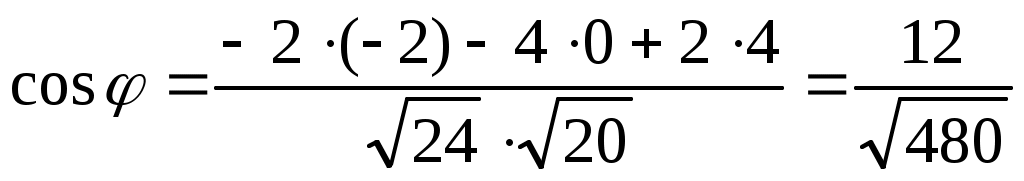
3) уравнение грани М1М2М3
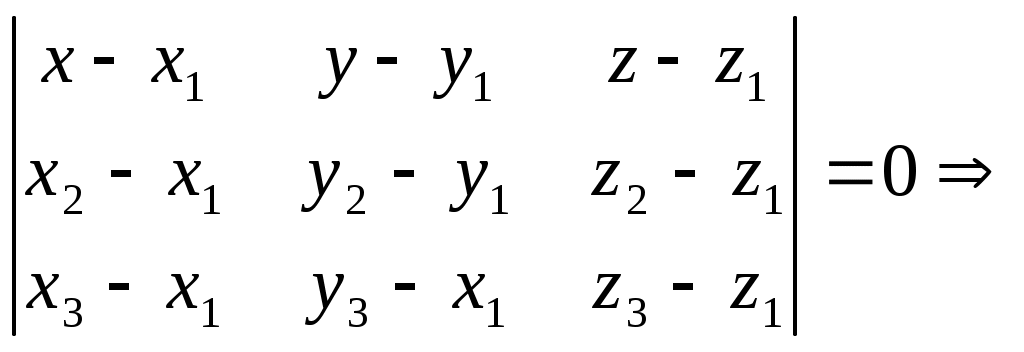
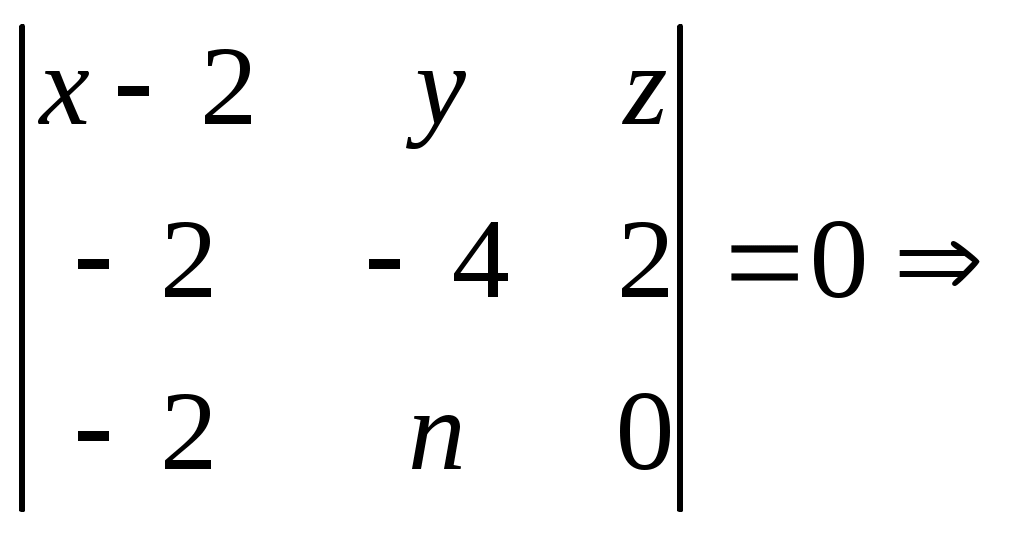
0-2nz-4y-8z-0-2n(x-2)=0 -2nx-4y-(8+2n)z+4n=0 nx+2y+(4+n)z-2n=0
Нормальный вектор плоскости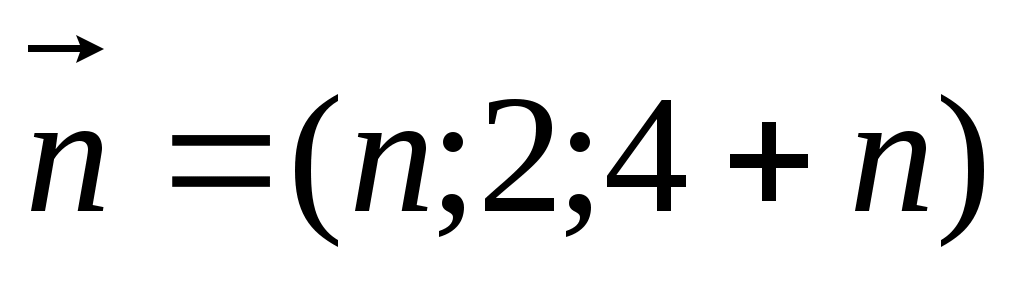
4) площадь грани М1М2М3
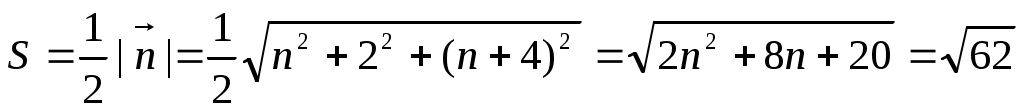
5) объём пирамиды.
Используем геометрический смысл смешанного произведения:
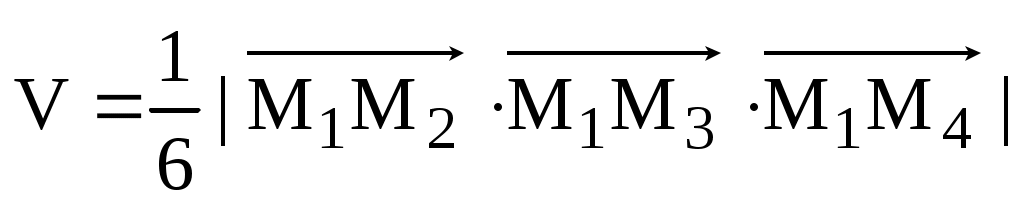
Координаты векторов:
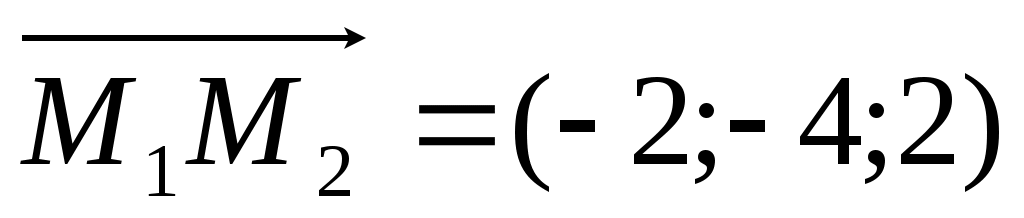 ,
, 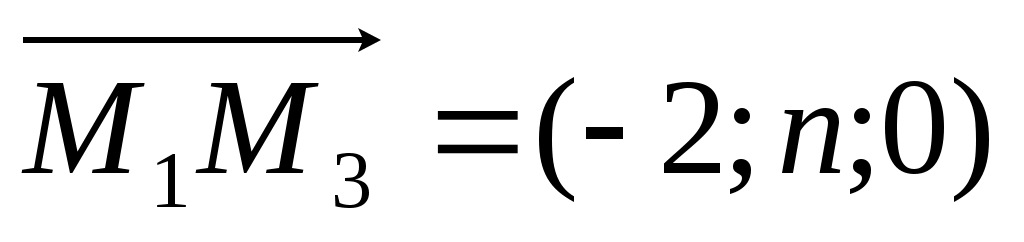 ,
, 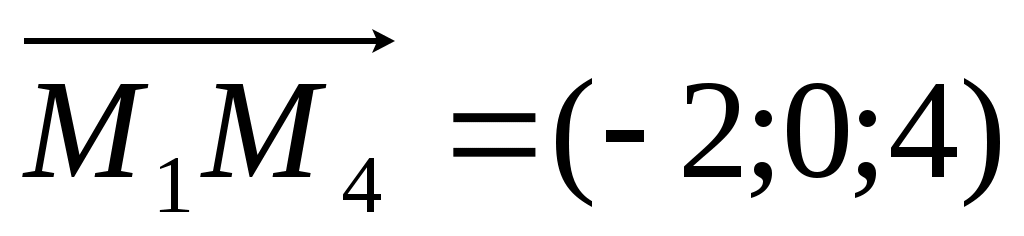
Найдем смешанное произведение
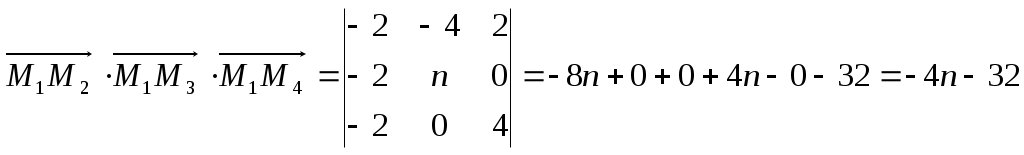 .
.
Тогда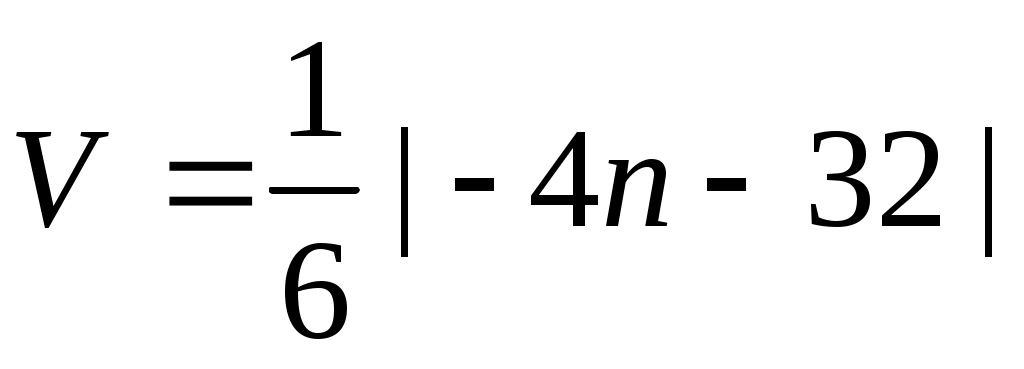
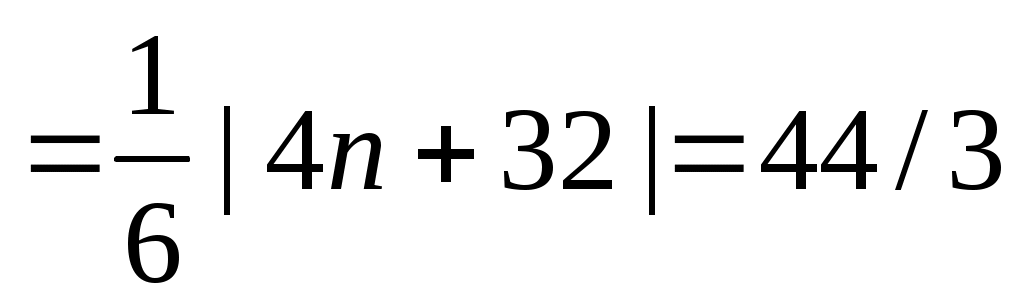
Задача 7. Найдите пределы: а)
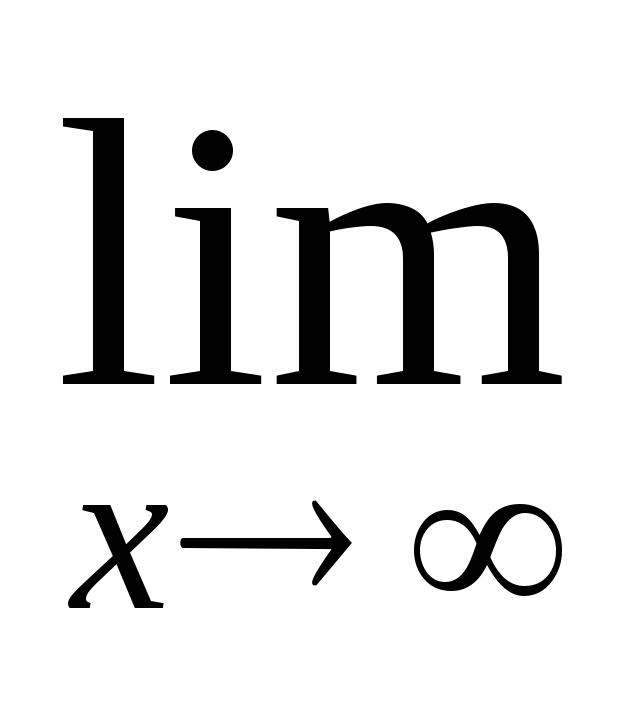
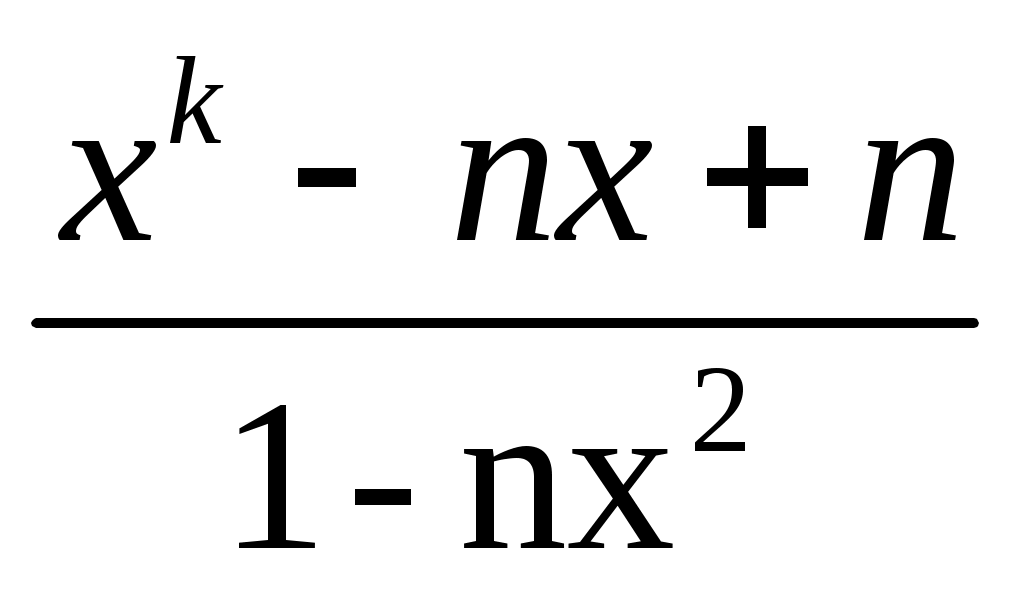 при k=0; 2 б)
при k=0; 2 б) 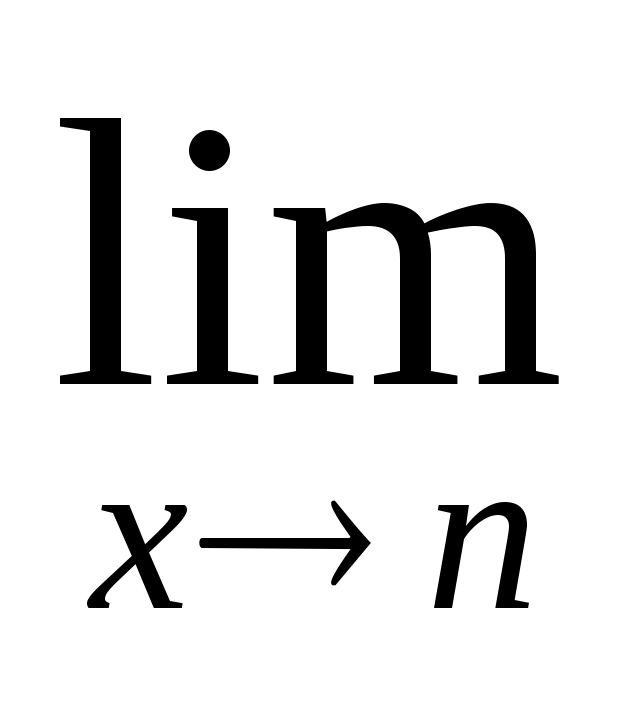
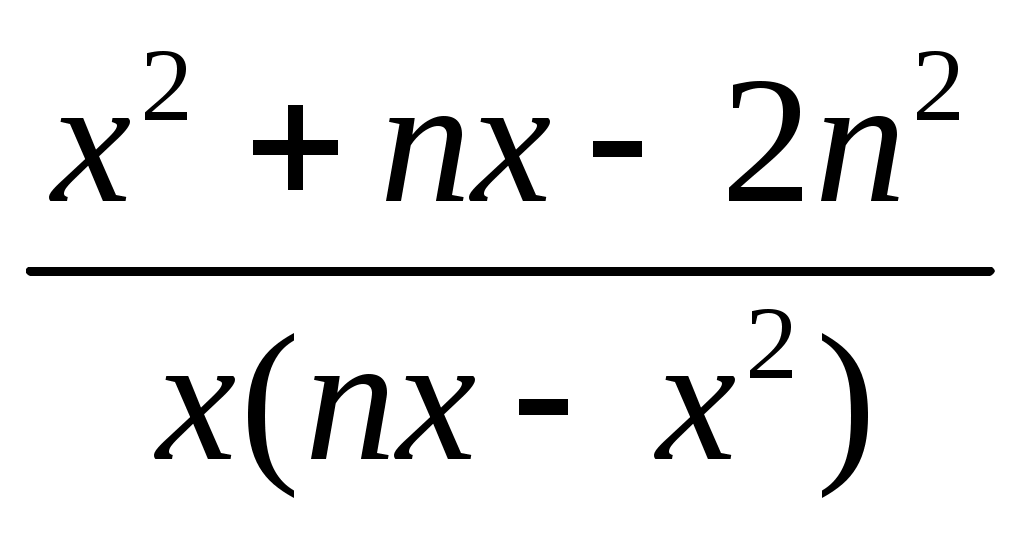 ,
,
в)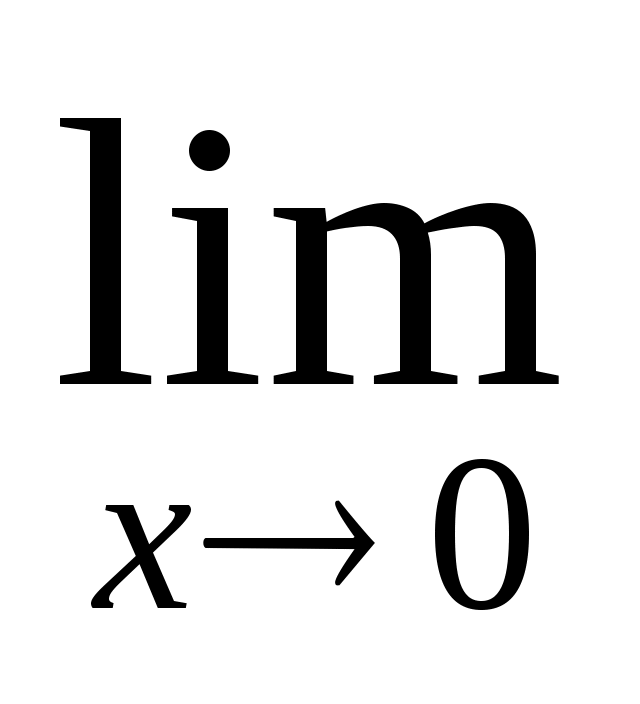
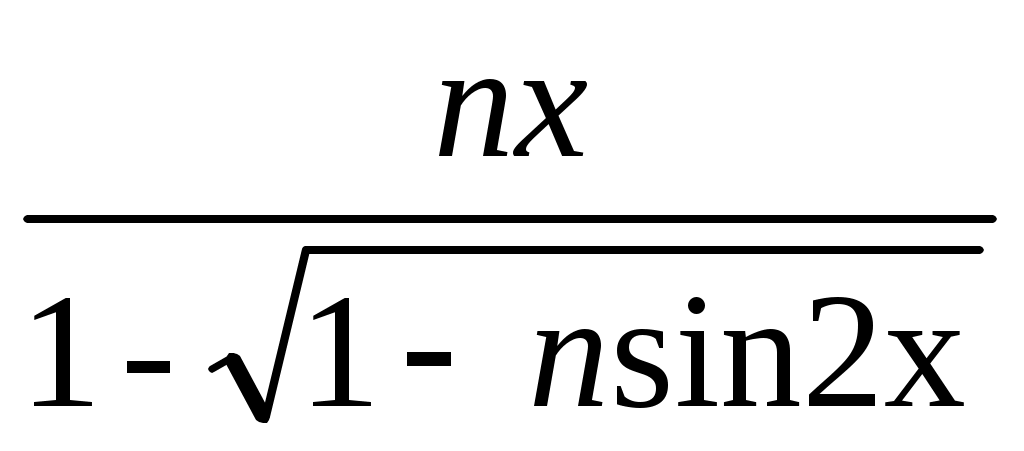 г)
г) 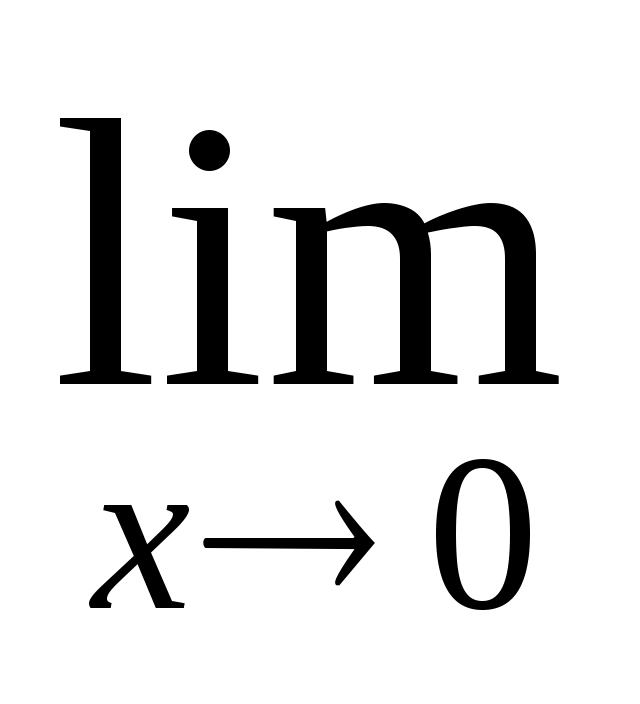
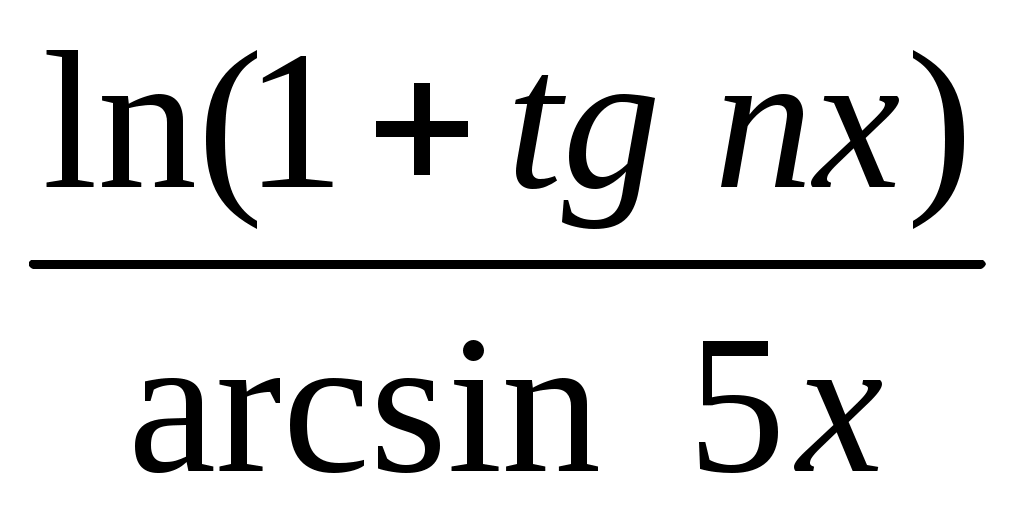
Решение
а)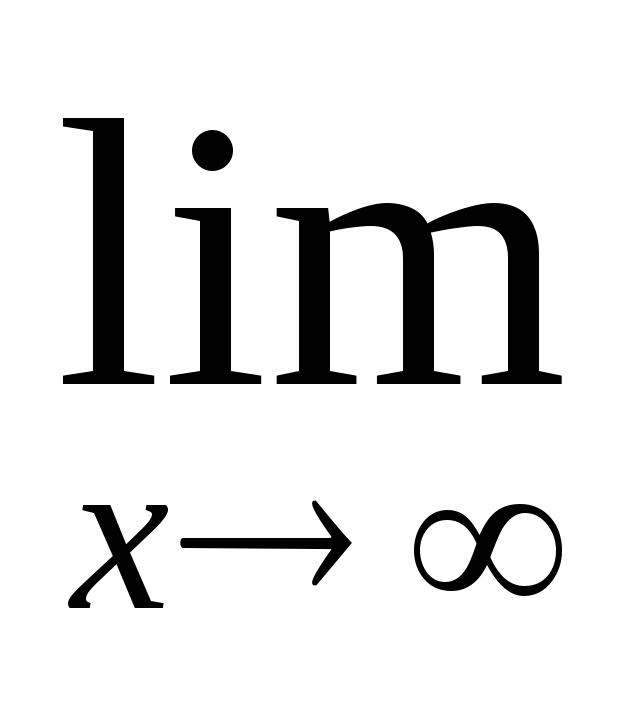
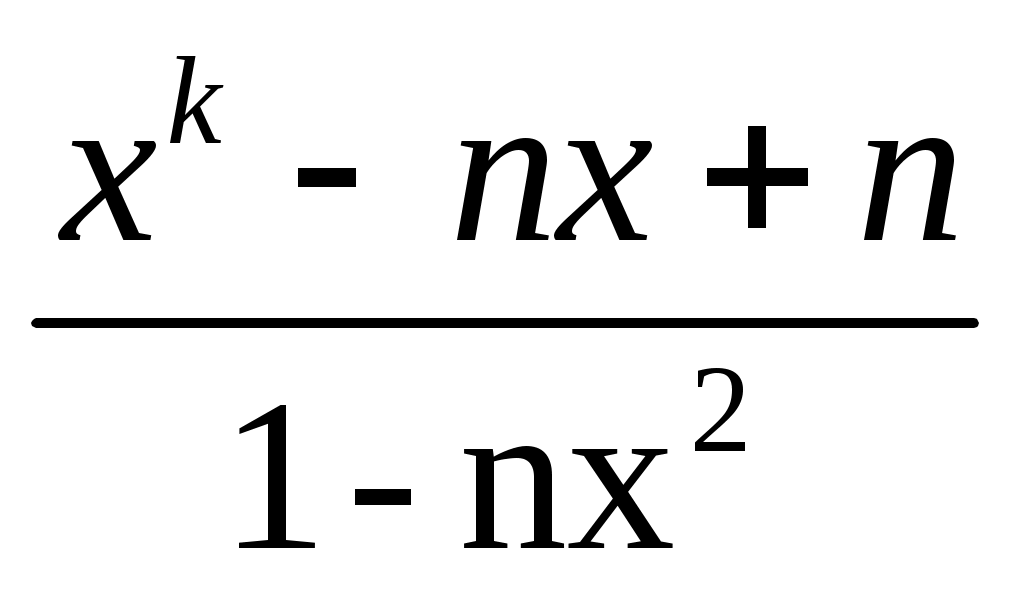 при k=0; 2
при k=0; 2
при k=0
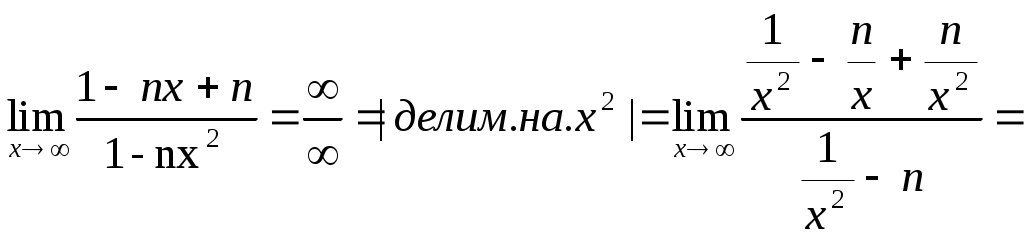
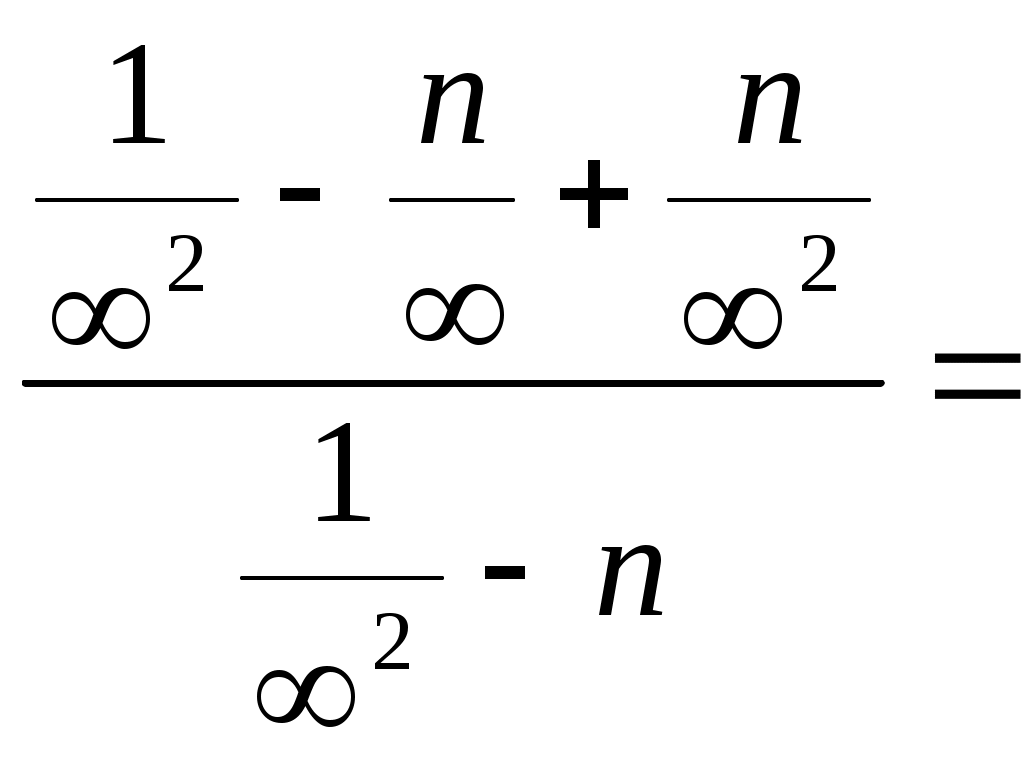
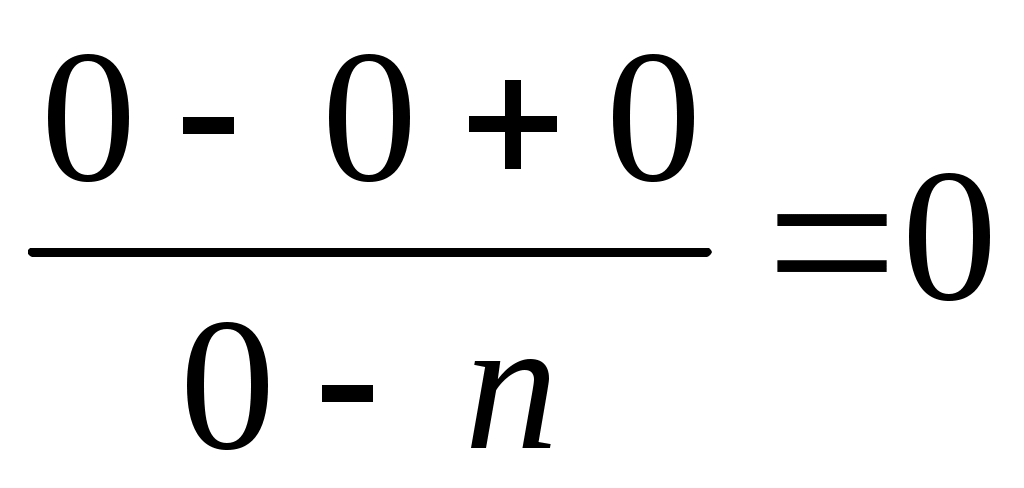
при k=2
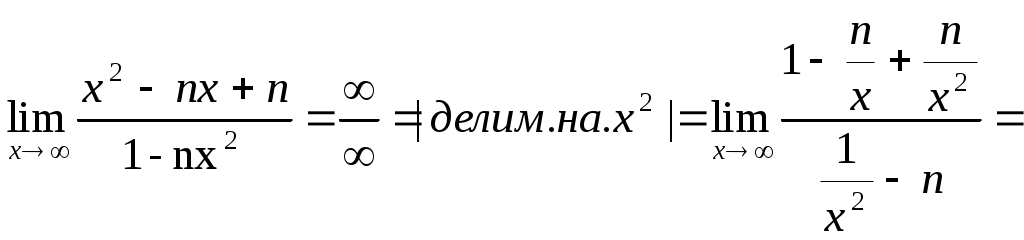
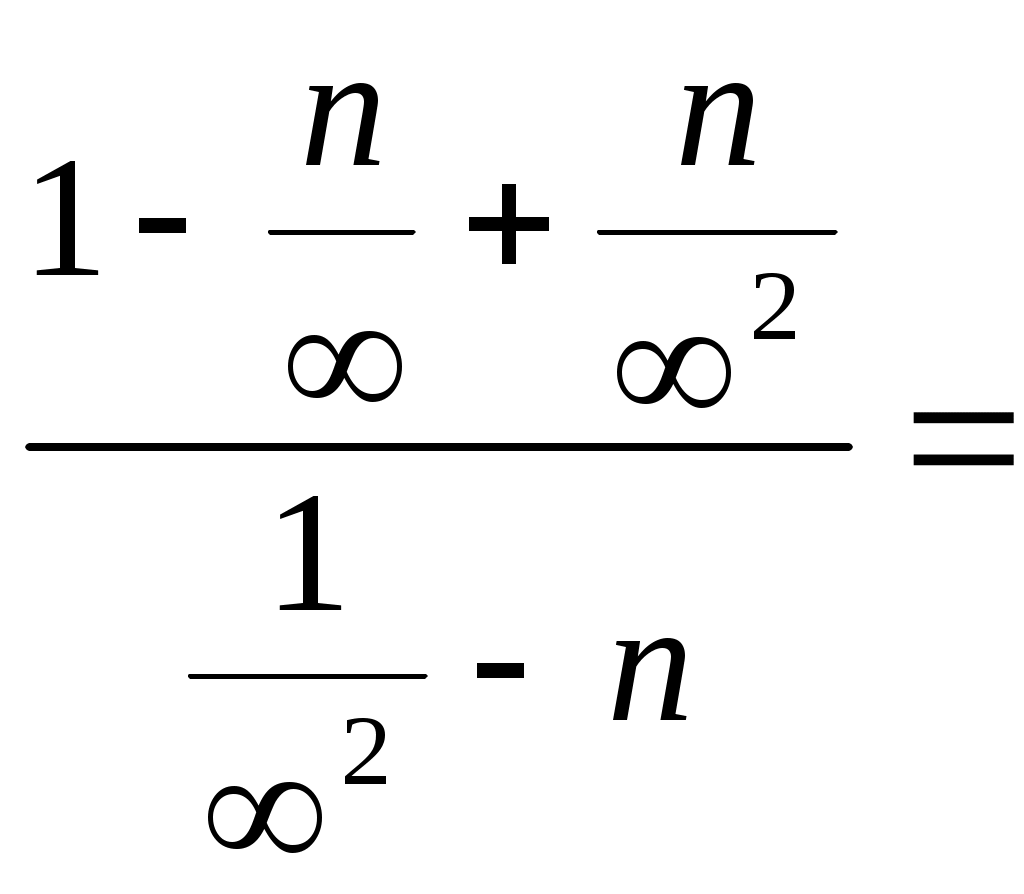
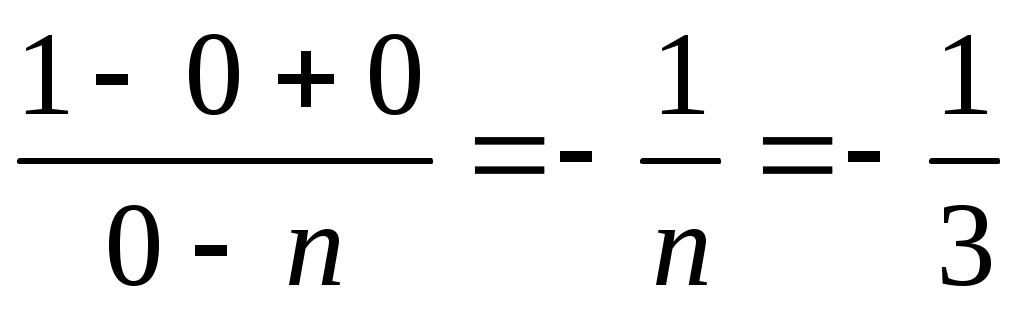
б)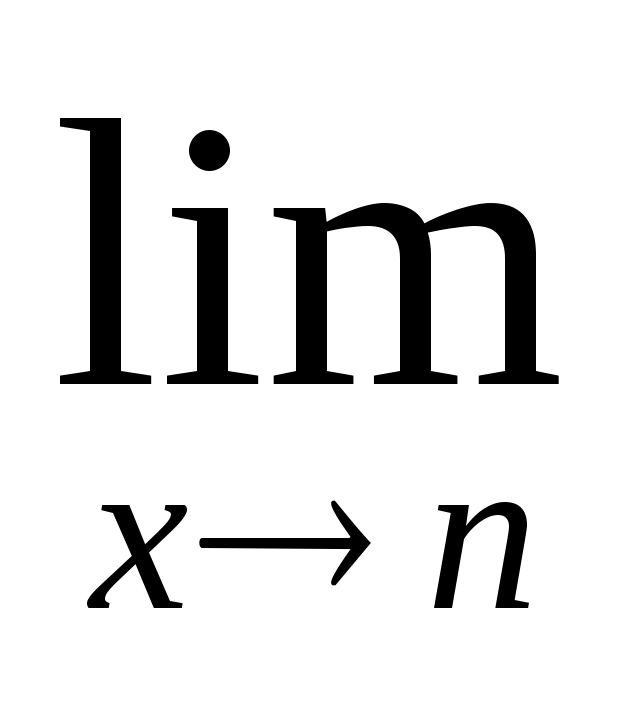
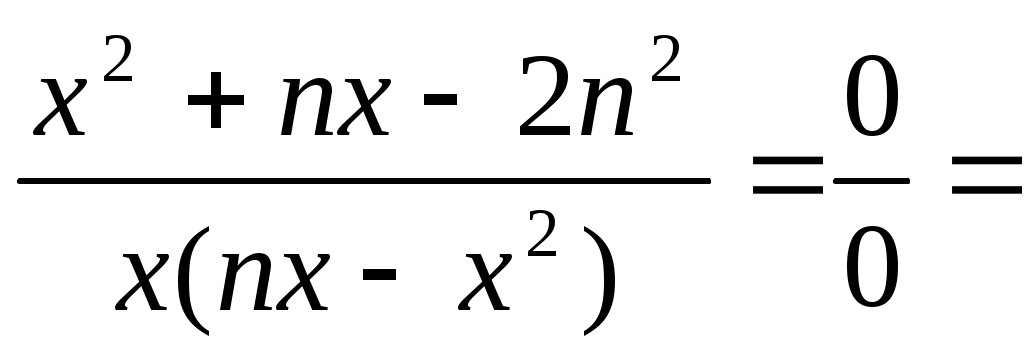
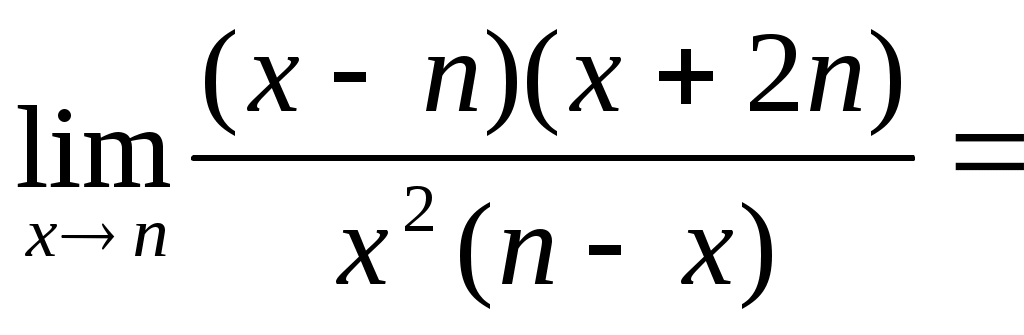
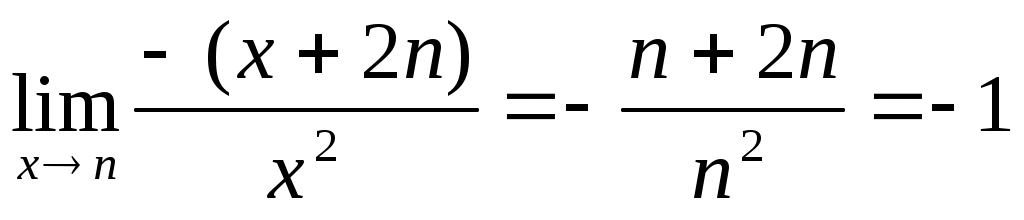
в)
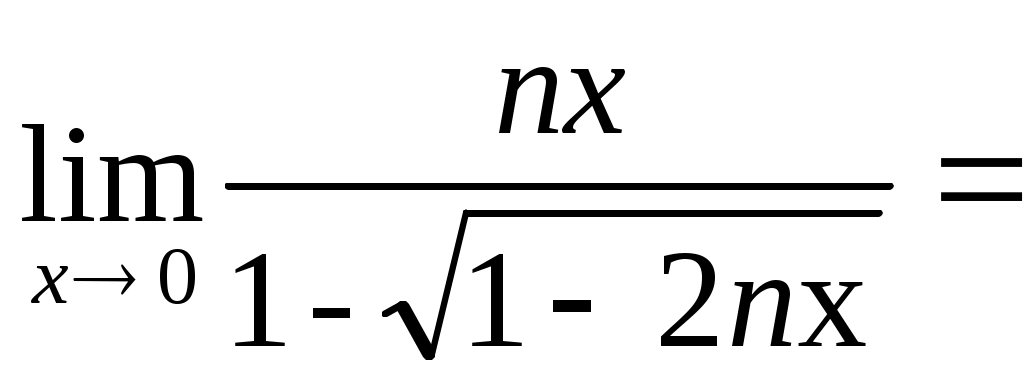
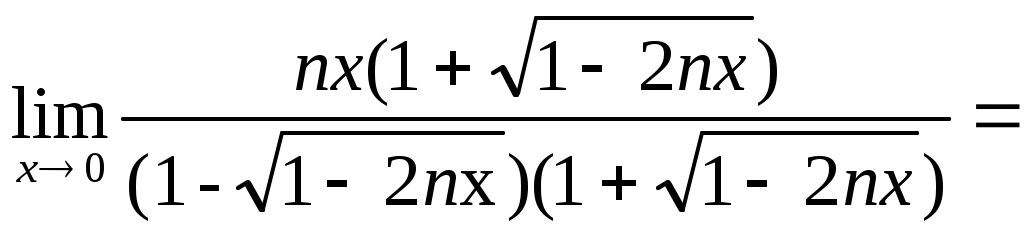
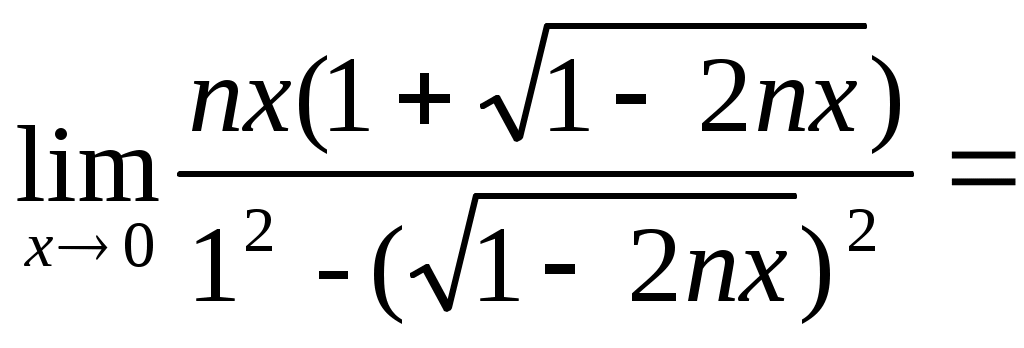
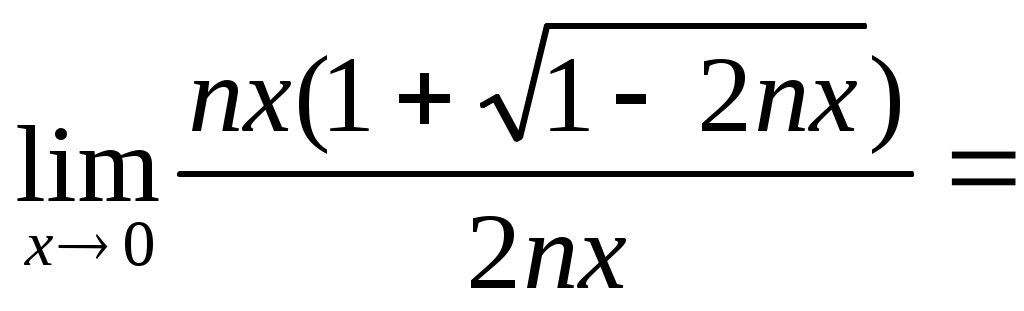
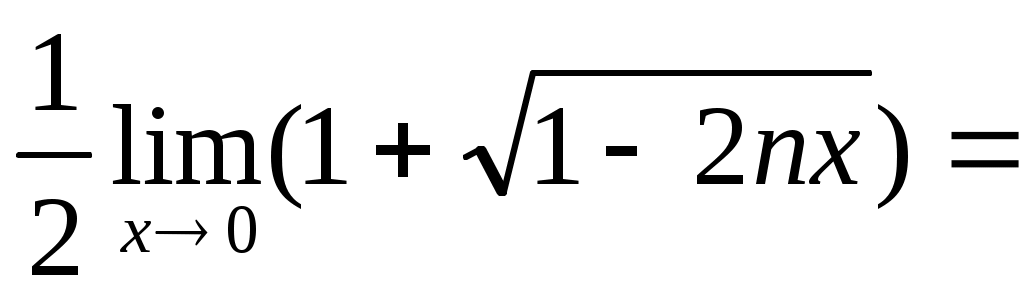
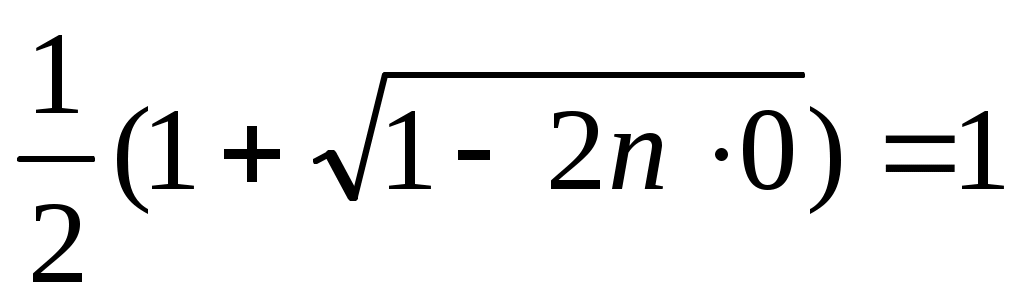
г)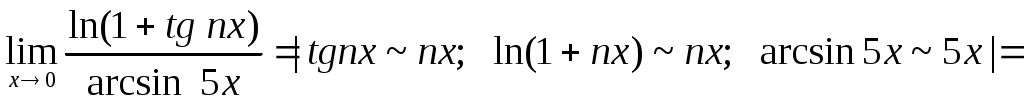
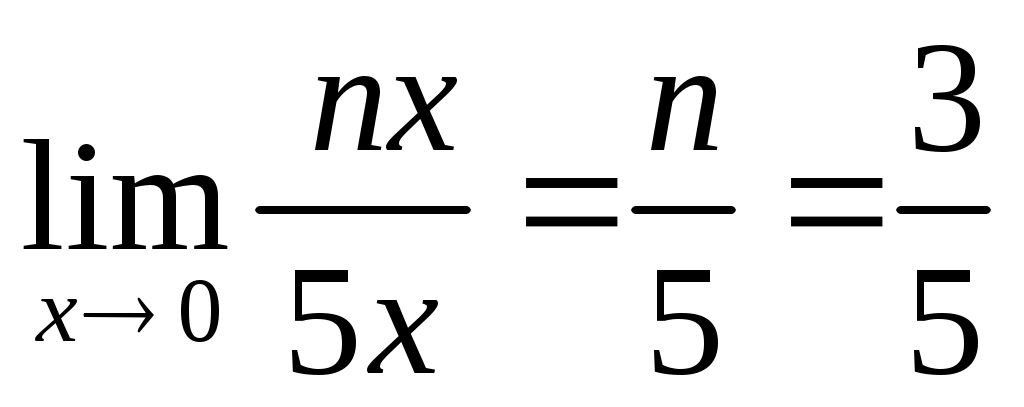
Задача 8. Исследуйте функцию на непрерывность графически. Определите характер
точек разрыва с помощью односторонних пределов.
Варианты 1-15.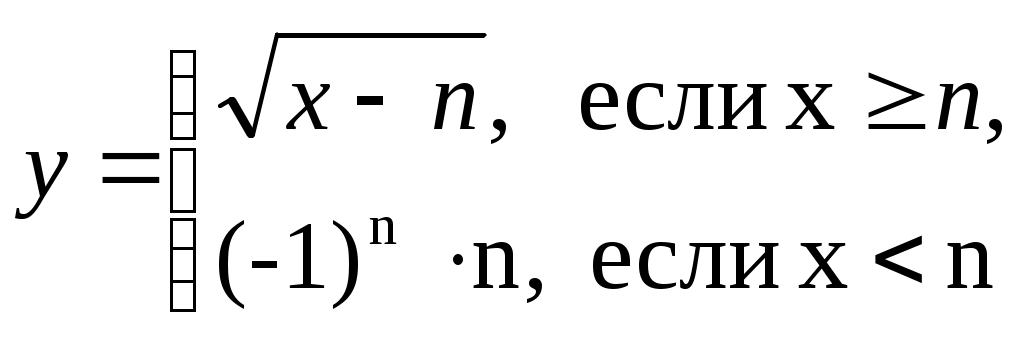
Решение
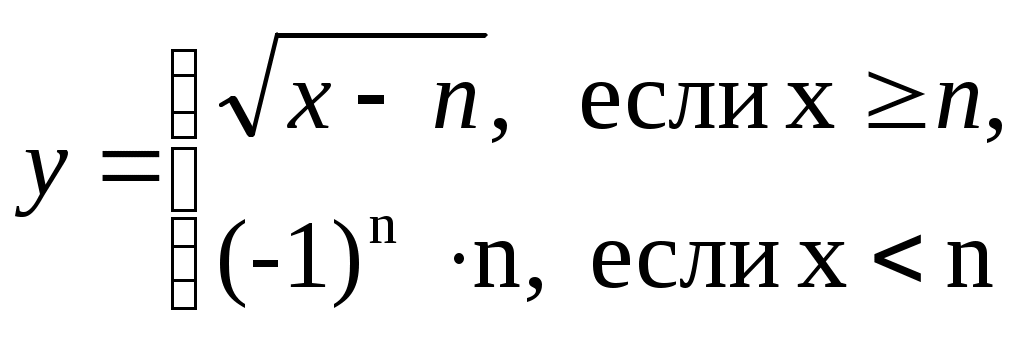
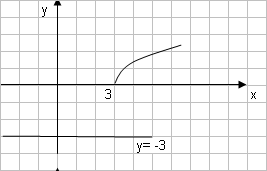
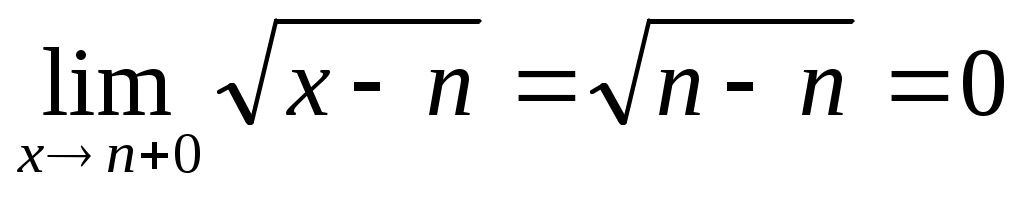
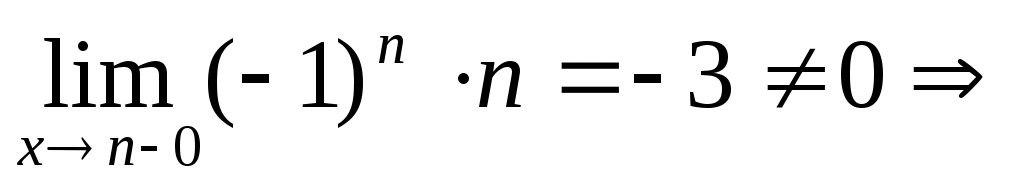
Односторонние пределы конечны и не равны, поэтому x=n=3 – точка разрыва 1 рода.
Задача9*. Запишите комплексное число в алгебраической, тригонометрической.
Варианты 1-15.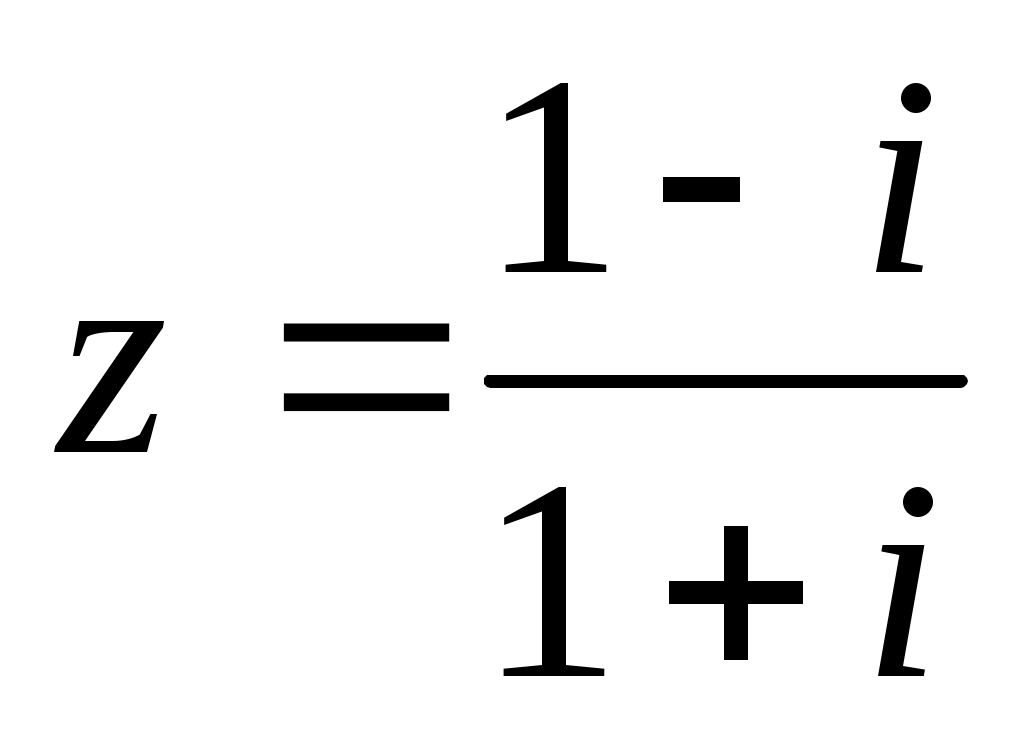
Решение
Алгебраическая форма:
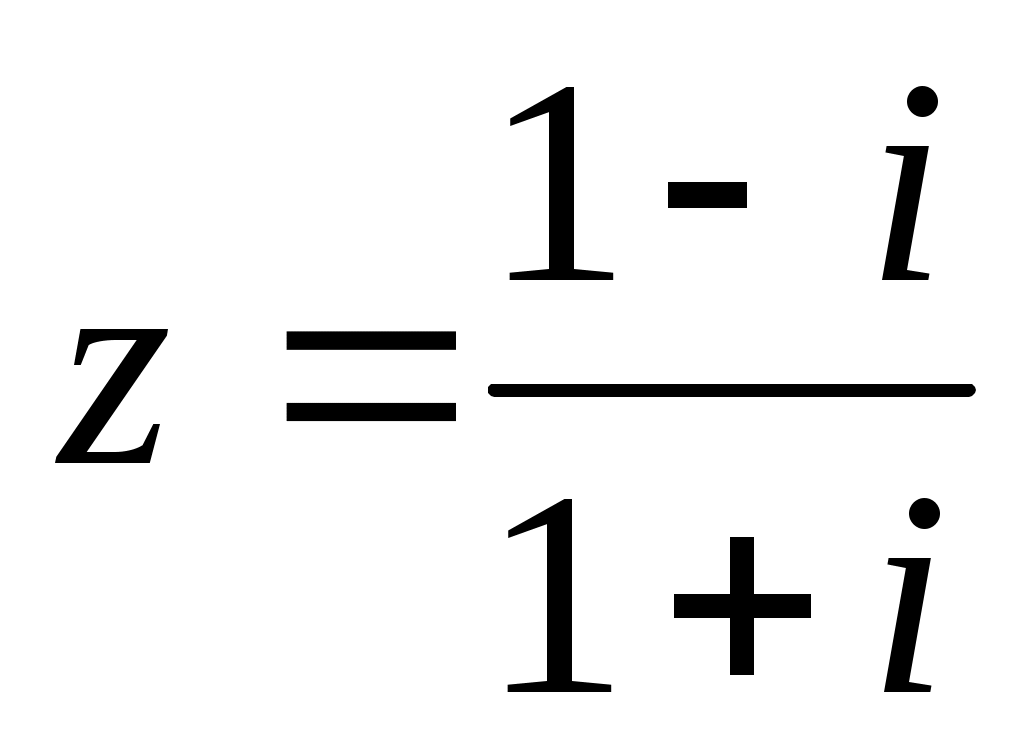
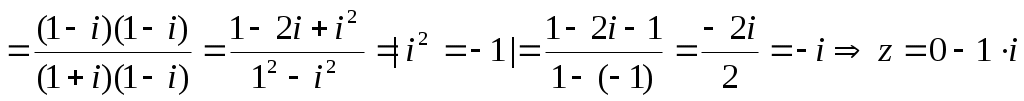
Тригонометрическая форма:
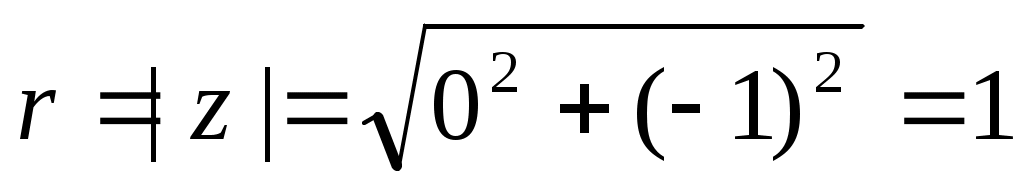
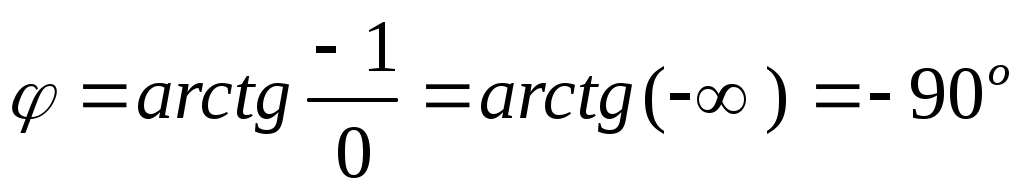
z=1(cos(-90o)+isin(-90o)) z=cos90o - isin90o
Задача 10. Найдите производные и дифференциалы 1 порядка.
Варианты 1-5, 11-20. а) у = (n-2x)e n-x, б) y = ln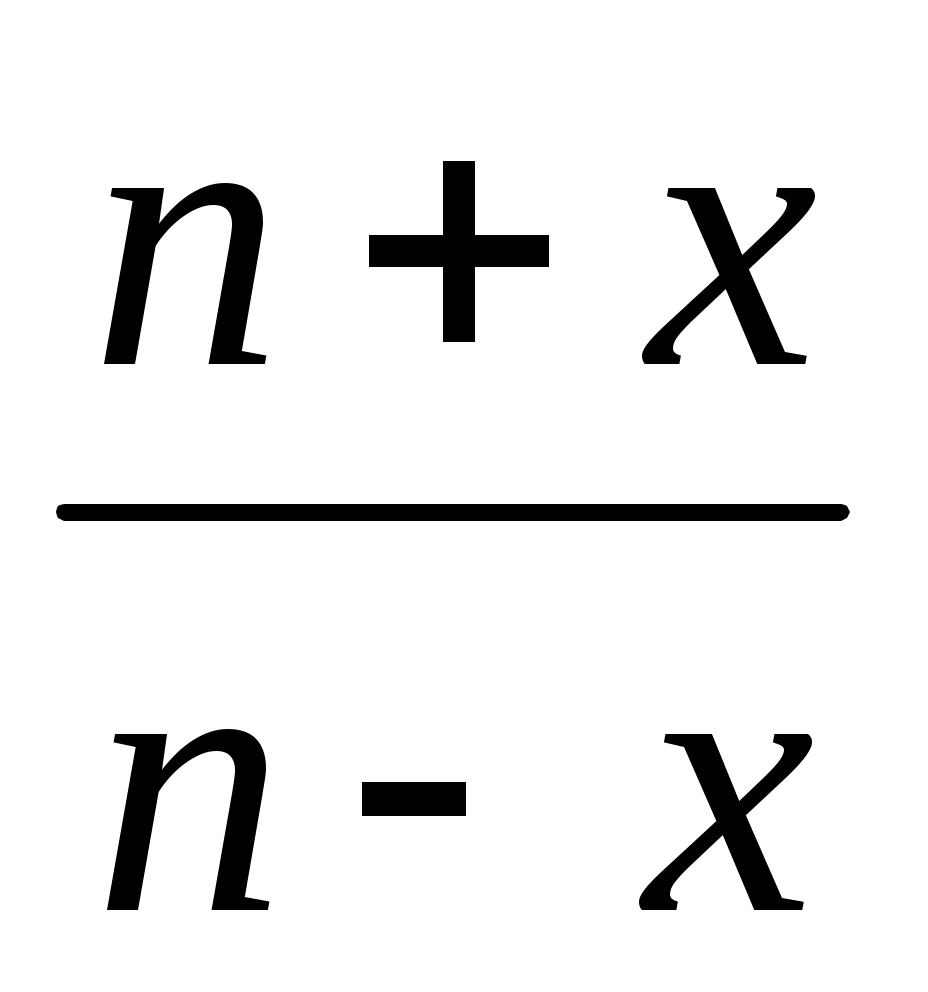
Решение
а) Применим правила дифференцирования произведения и сложной функции:
у / = (n-2x)/ e n-x + (n-2x) (e n-x ) / = -2 e n-x + (n-2x) e n-x (n-x)/ =
= -2 e n-x + (n-2x) e n-x (-1) =(2x-n-2) e n-x = (2x-5) e 3-x
dy=f /(x)dx= (2x-5) e 3-x dx
б) Применим правила дифференцирования частного и сложной функции:
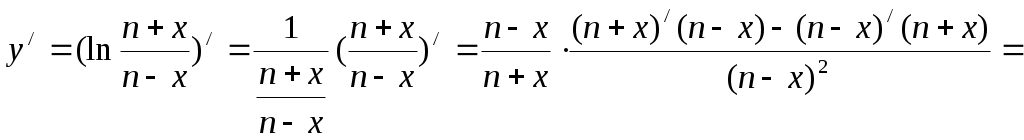
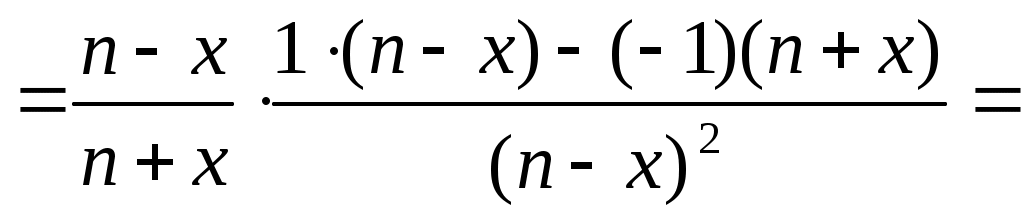
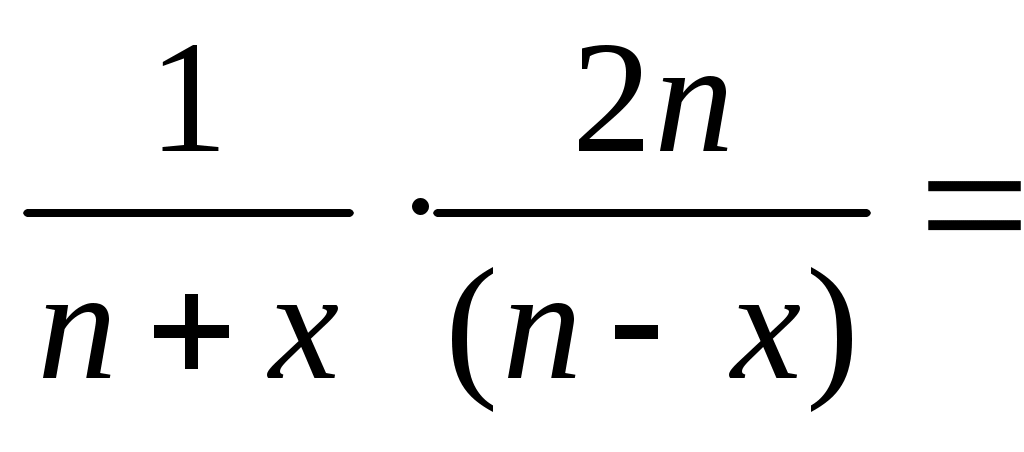
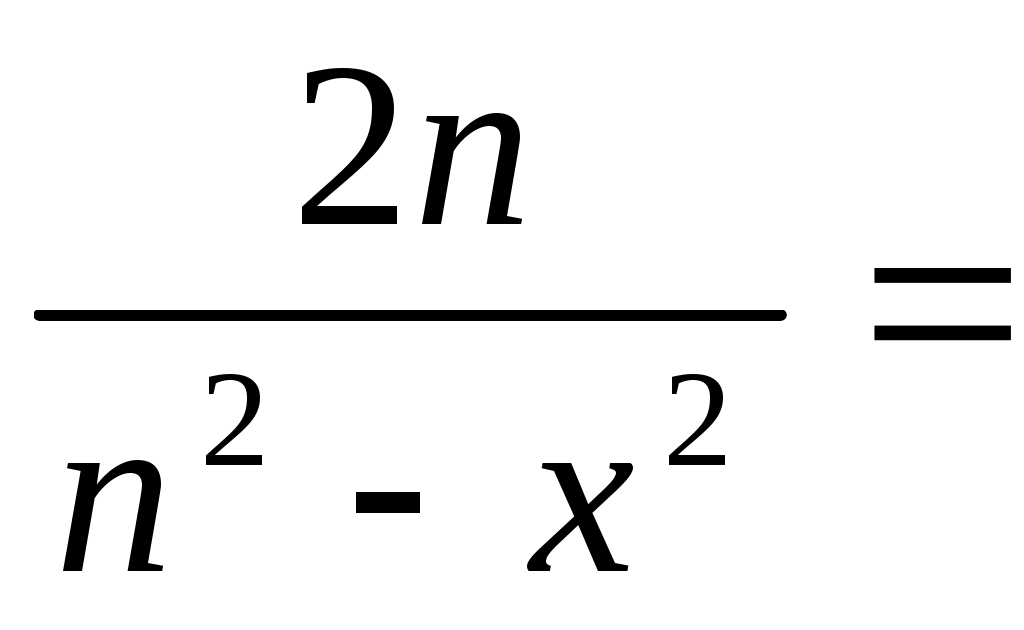
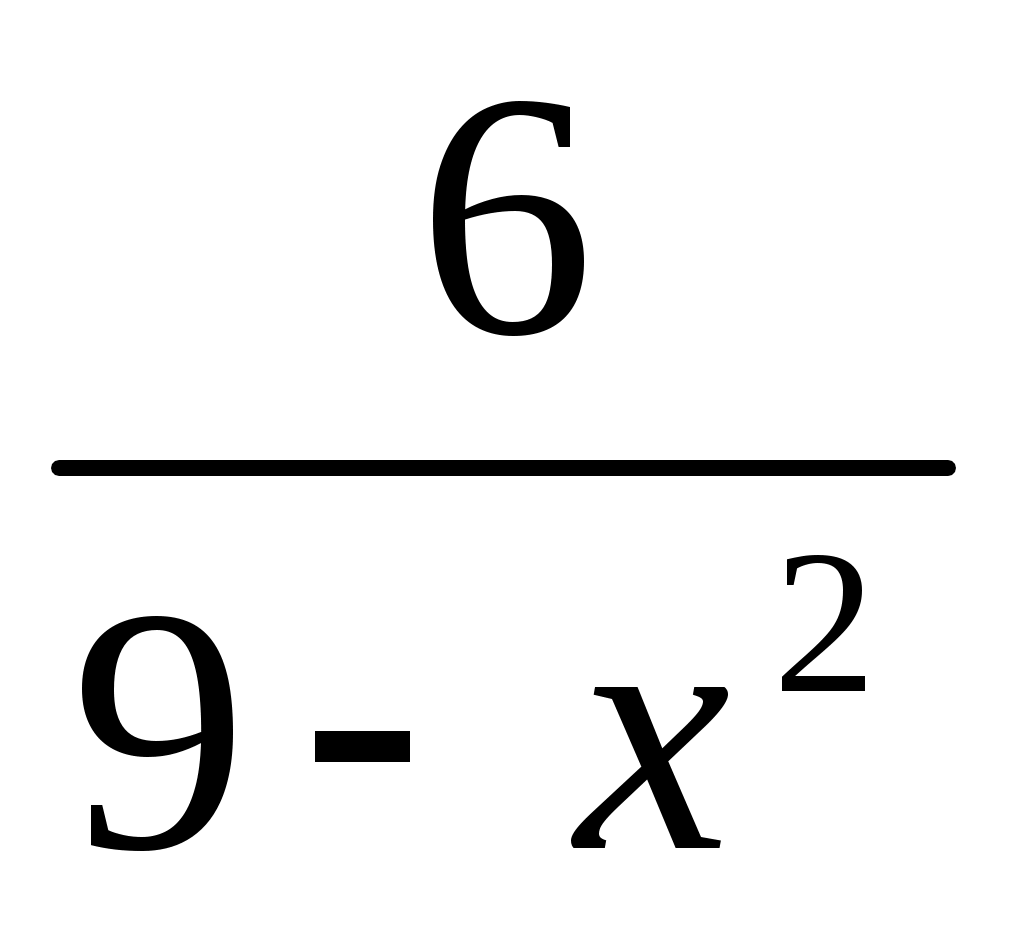
dy=f /(x)dx= dx
dx
Задача 11. Найдите пределы по правилу Лопиталя:
Варианты 1-5 а)
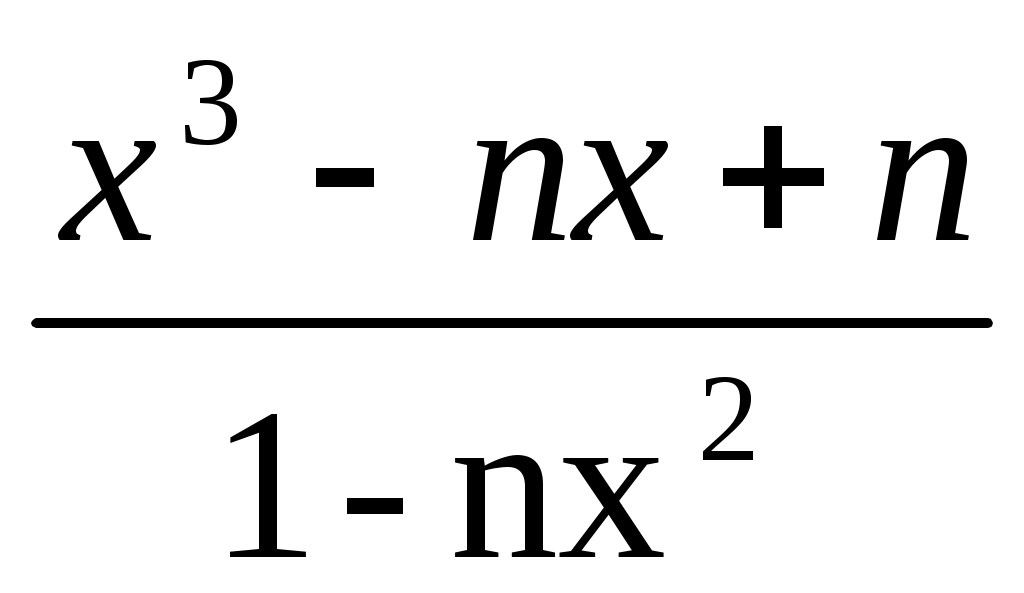 , б)
, б) 
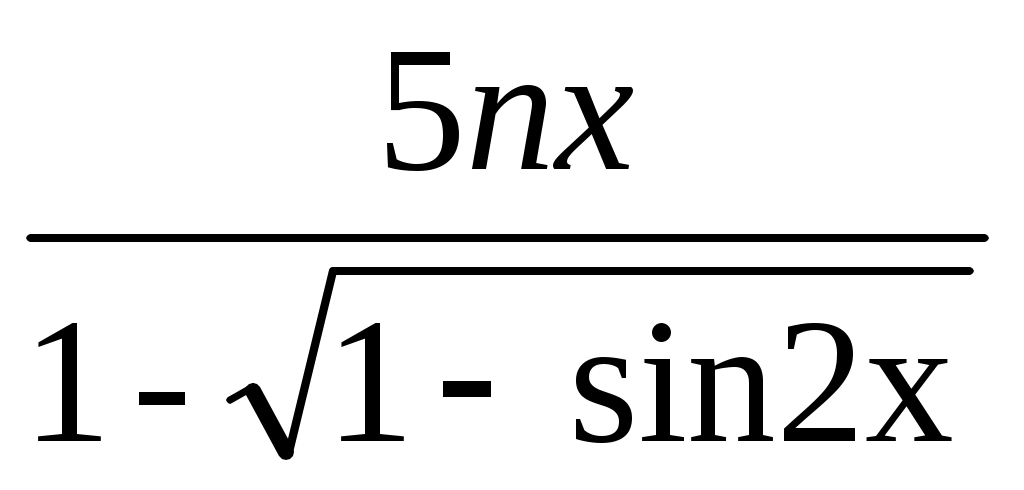
Решение
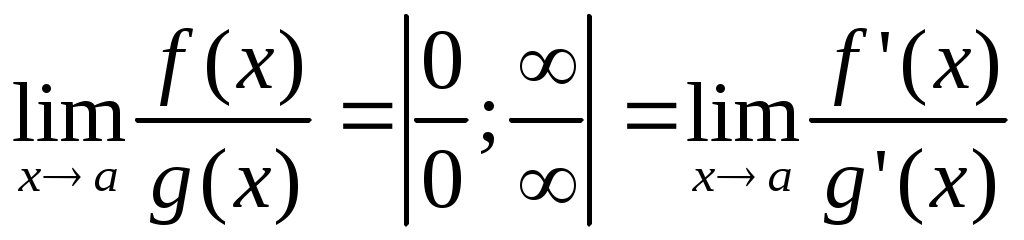
а)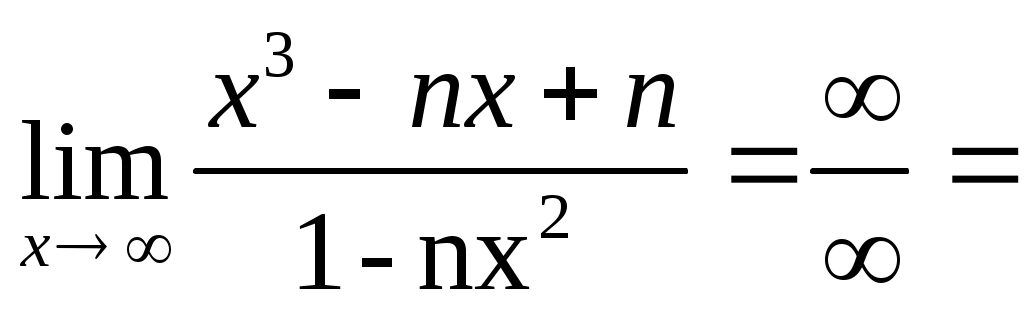
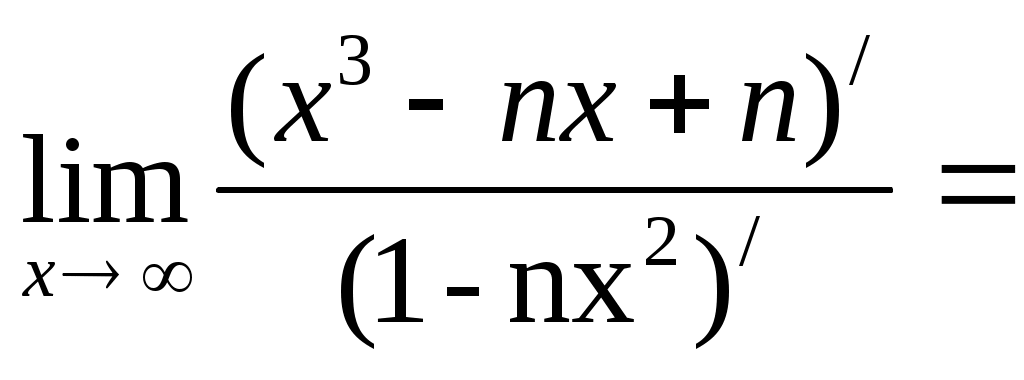
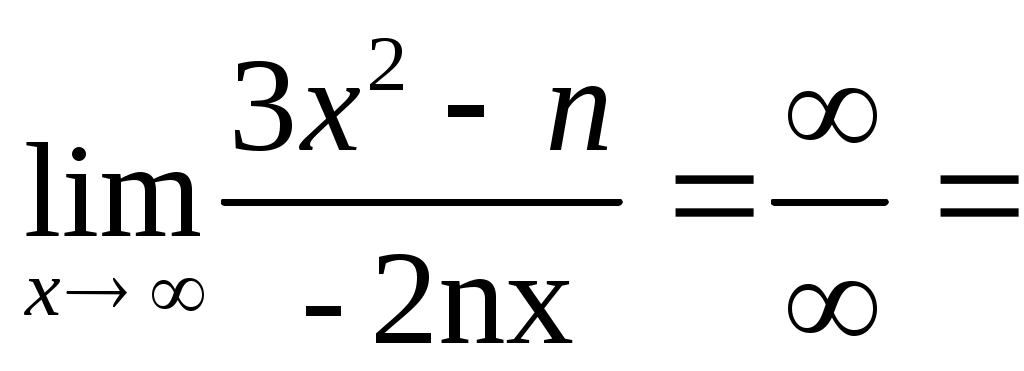
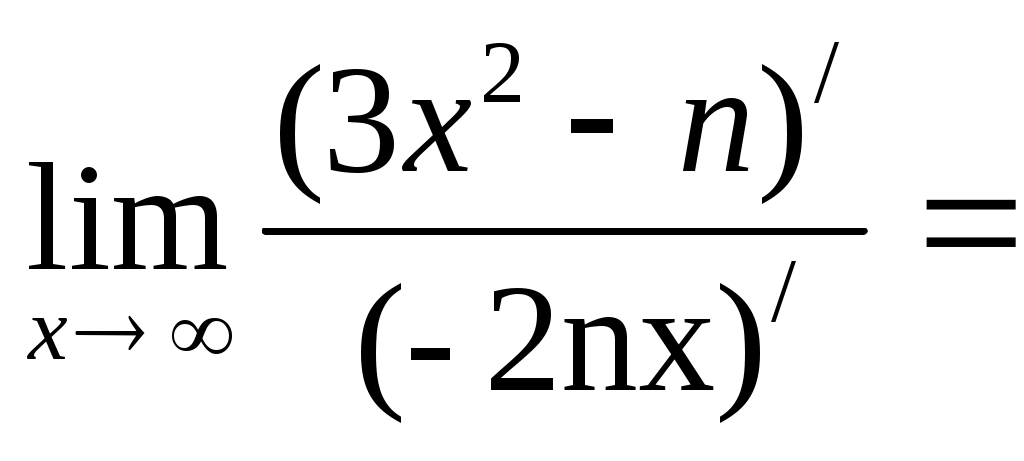
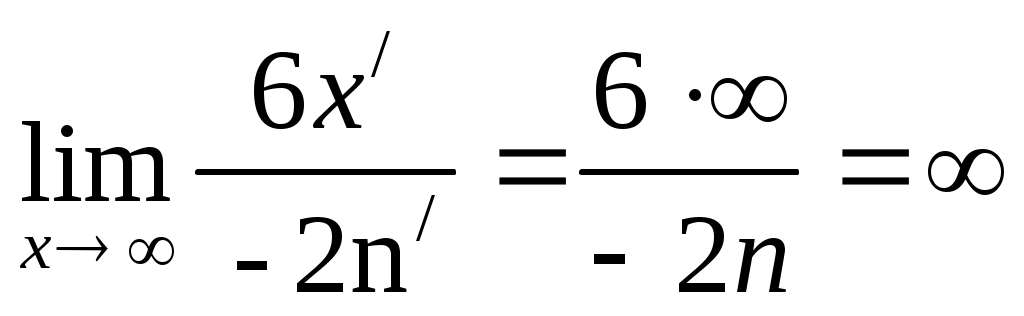
б)
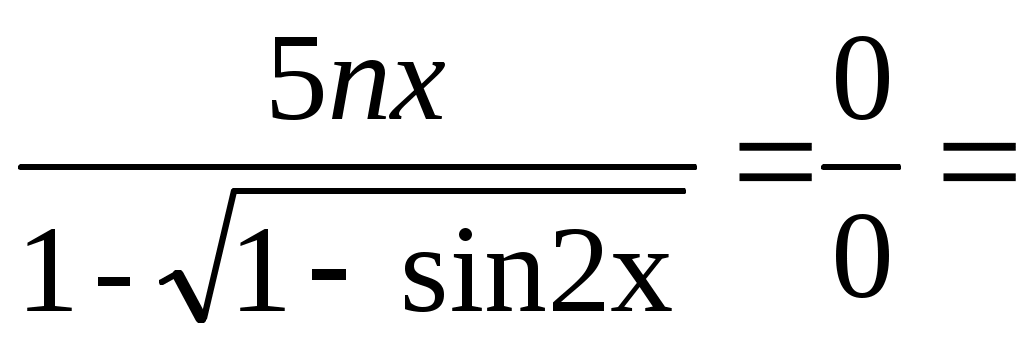
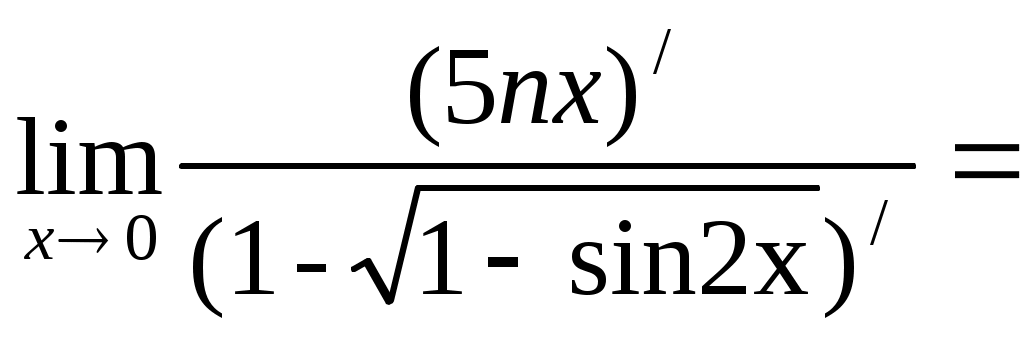
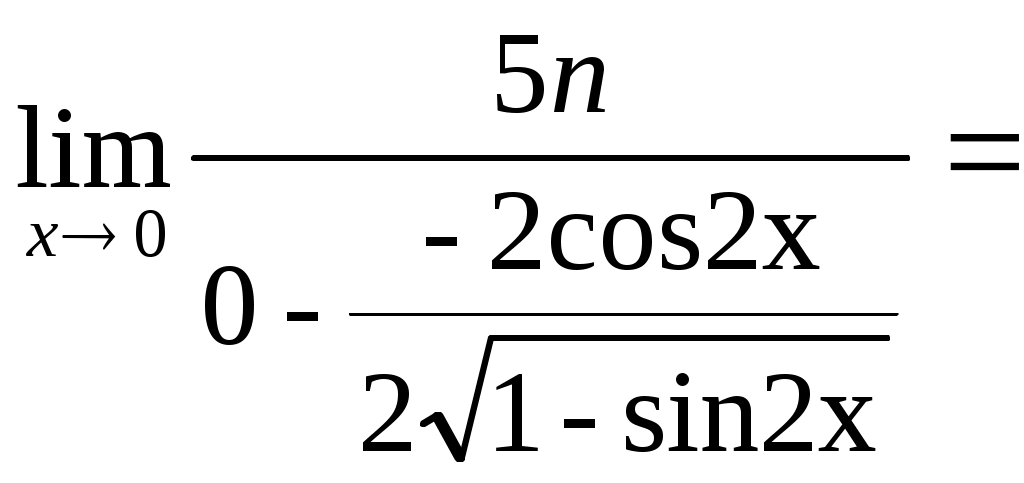
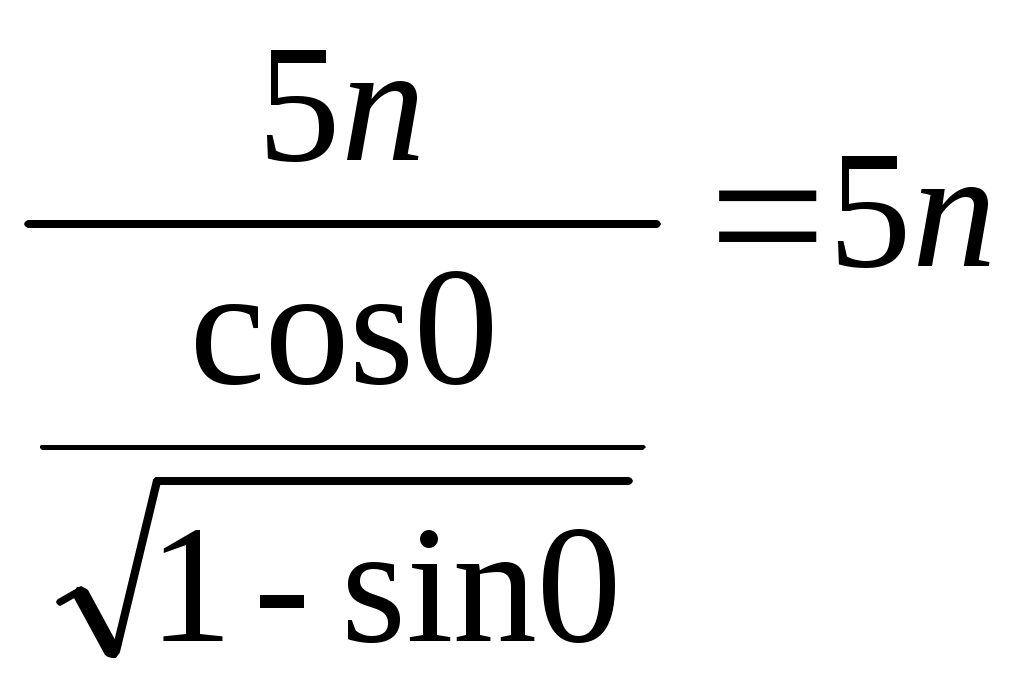 =15
=15
Задача 12. Найдите уравнение касательной к графику функции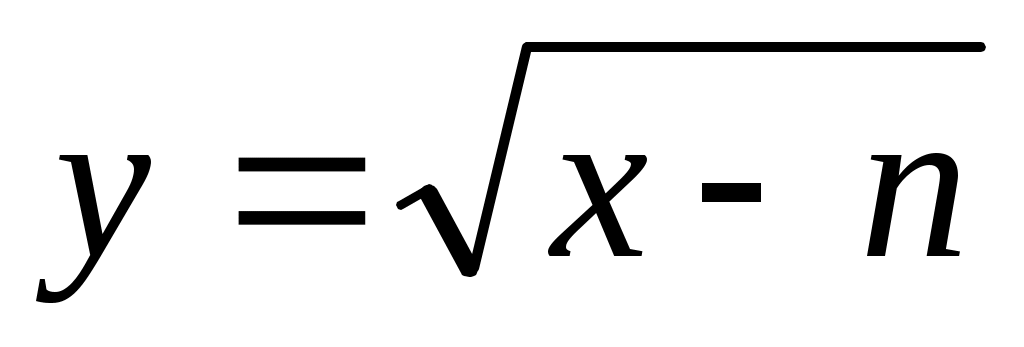 в точке хо=n+1.
в точке хо=n+1.
Сделайте чертеж.
Решение
Сделаем чертеж
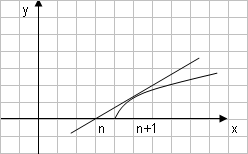
Уравнение касательной к графику функции y=f(x) в точке Mо(хо,уо) имеет вид:
у-f(xо)= f ’(xo)(х-хо).
f(xо)=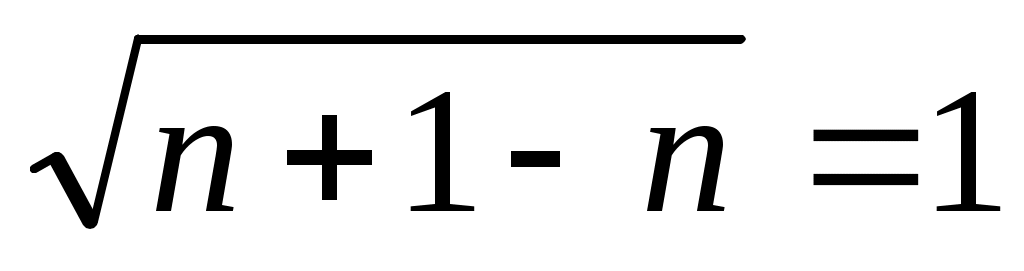
f ’(xo) =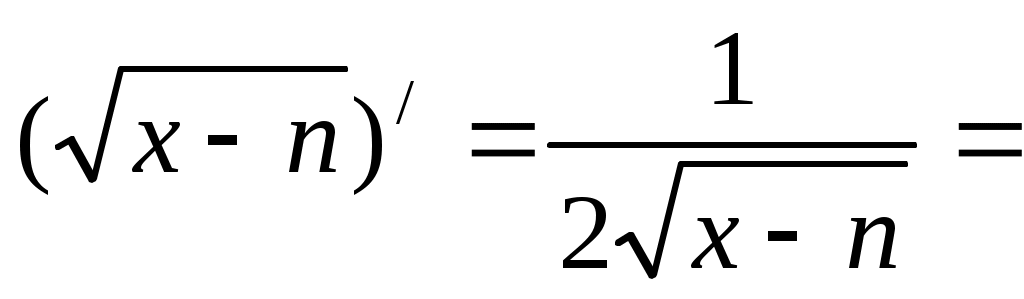
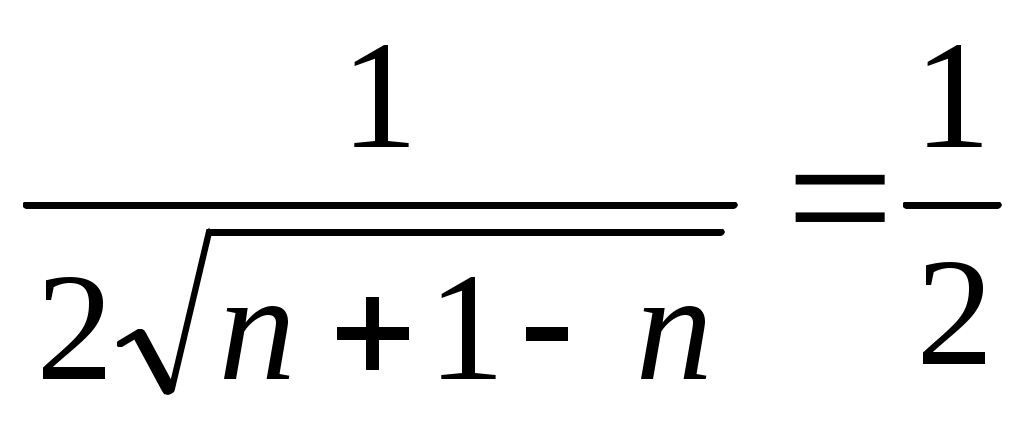
Уравнение касательной:
у-1= 0,5(х-n) y=0,5x+1-0,5n = 0,5x-0,5
Задача 13. Найдите наибольшее и наименьшее значения функции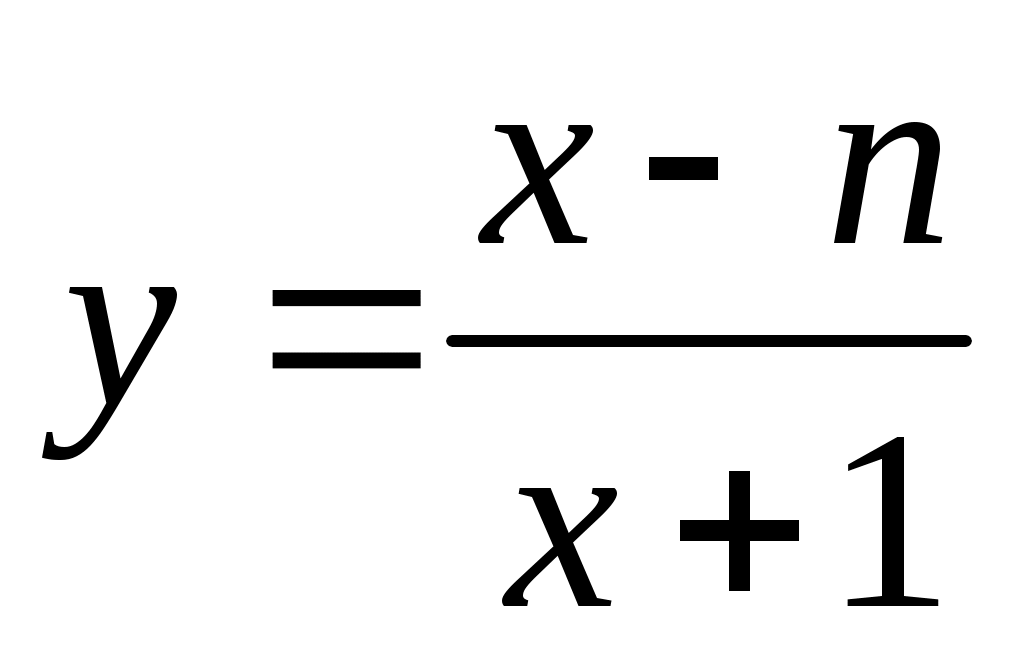 на отрезке [0,n].
на отрезке [0,n].
Решение
Найдем производную функции:
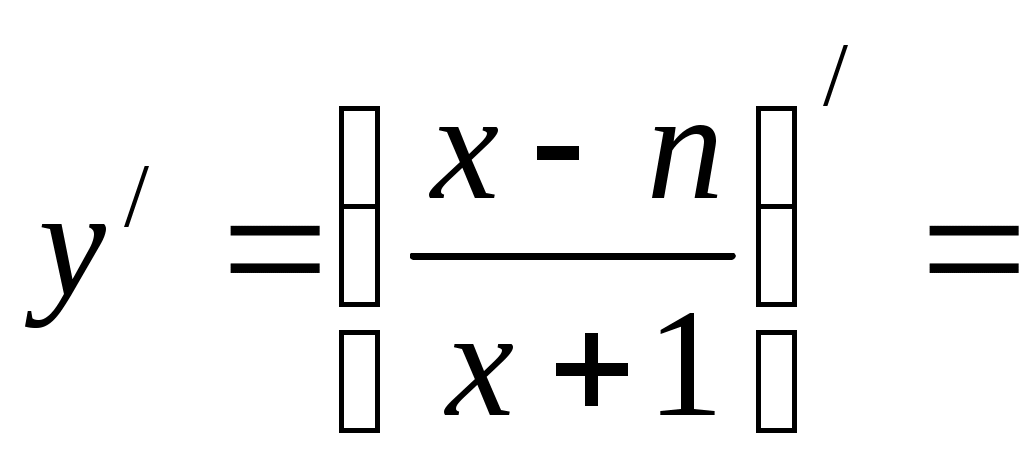
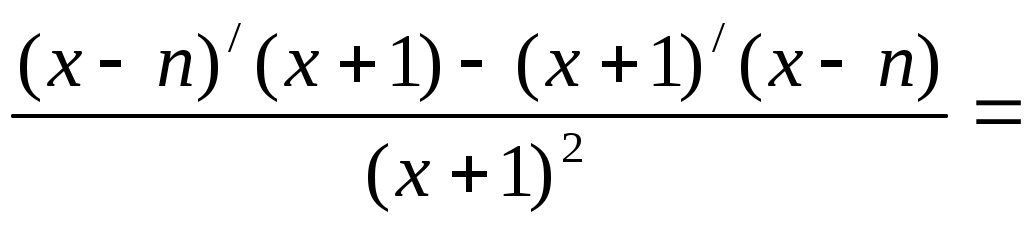
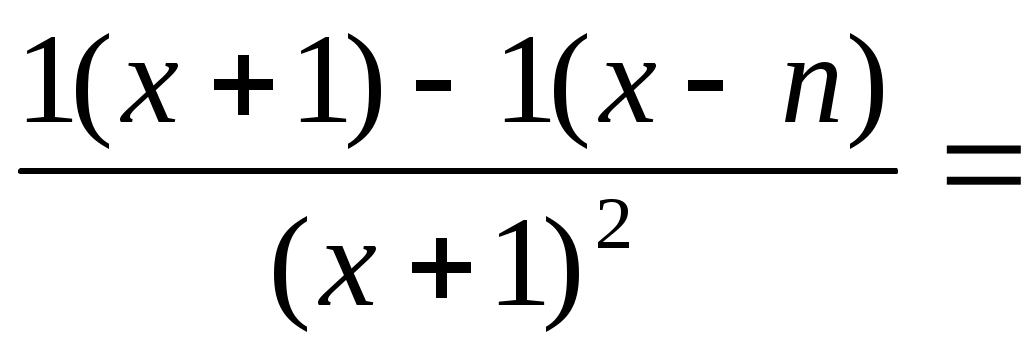
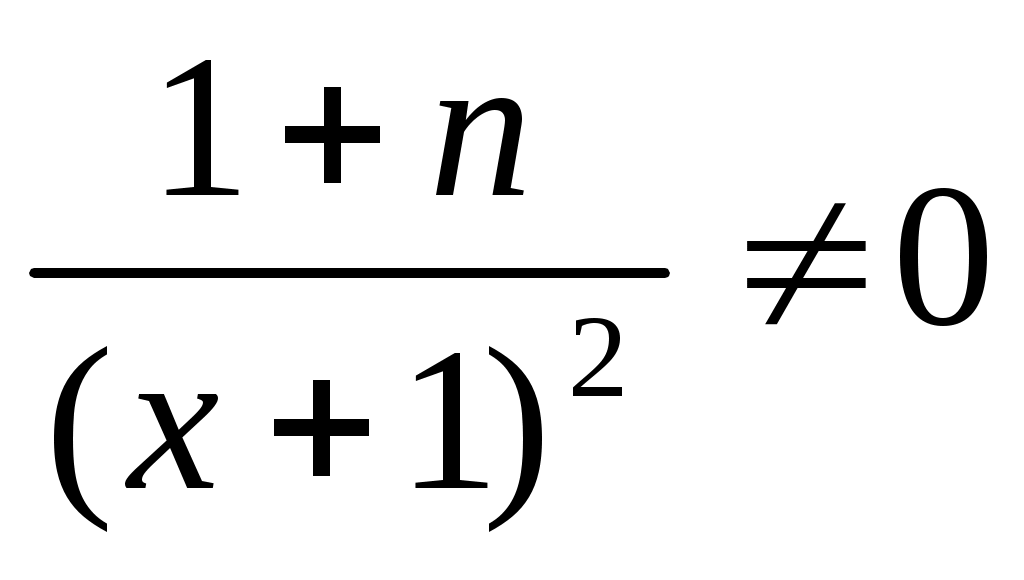
Производная не обращается в 0.
Производная не определена при x+1=0, откуда x=-1 – критическая точка вне отрезка [0,n].
Таким образом, наибольшее и наименьшее значения функции могут быть только на концах отрезка:
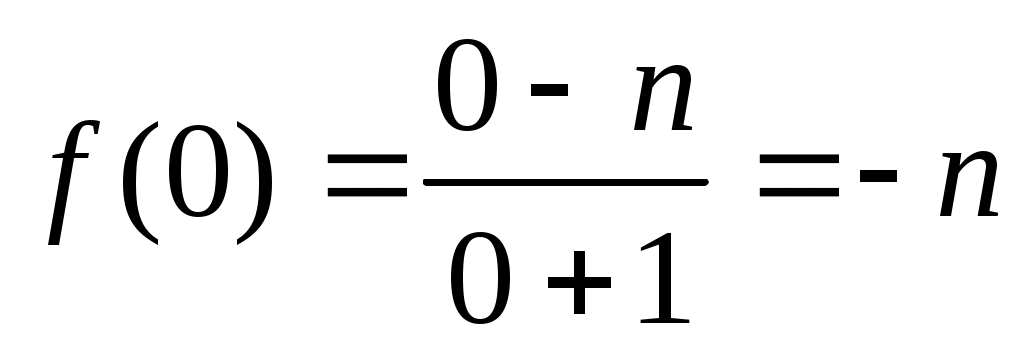 =-3
=-3
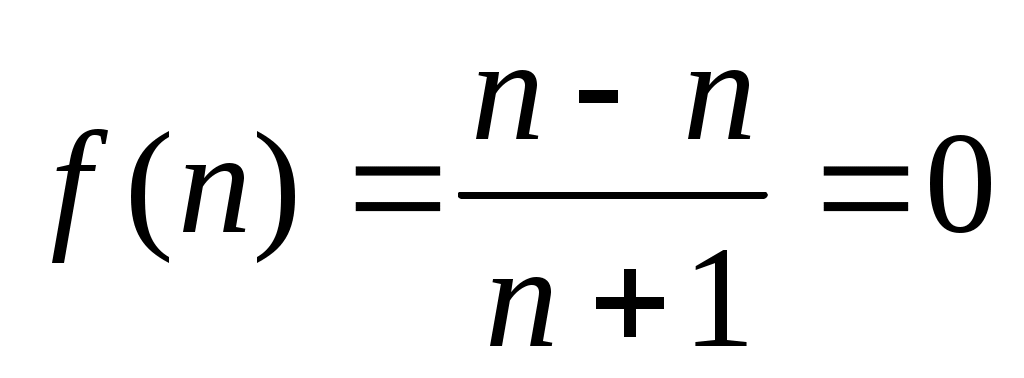
Наибольшее значение равно f(n)=0.
Наименьшее значение равно f(0)= -3.
получим:
Длина ребра М1М2 равна расстоянию между точками М1и М2 или длине вектора:
2) угол между рёбрами М1М2 и М1М4
Определим угол между сторонами М1М2 и М1М4 как угол между соответствующими векторами. Найдем координаты векторов:
3) уравнение грани М1М2М3
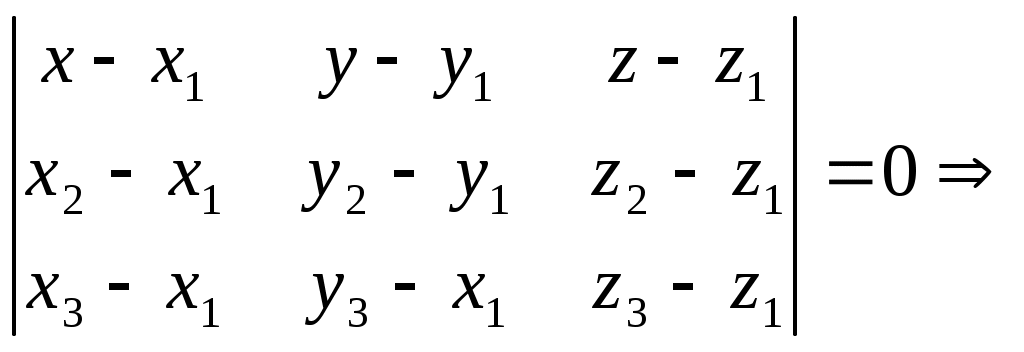
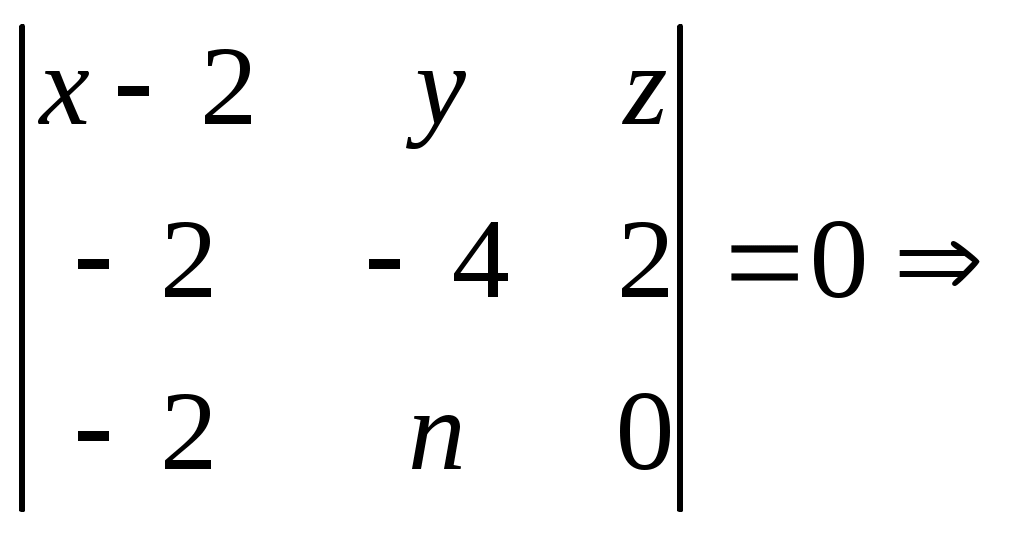
0-2nz-4y-8z-0-2n(x-2)=0 -2nx-4y-(8+2n)z+4n=0 nx+2y+(4+n)z-2n=0
Нормальный вектор плоскости
4) площадь грани М1М2М3
5) объём пирамиды.
Используем геометрический смысл смешанного произведения:
Координаты векторов:
Найдем смешанное произведение
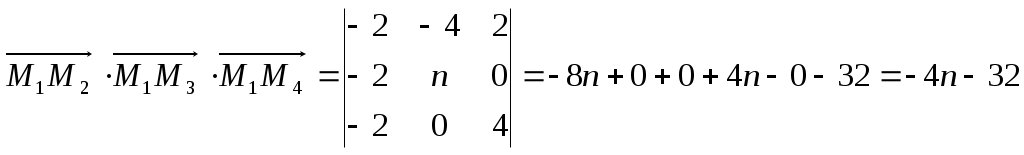 .
. Тогда
Задача 7. Найдите пределы: а)
в)
Решение
а)
при k=0
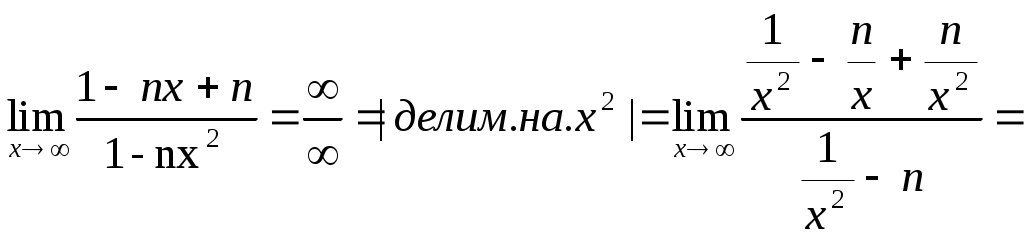
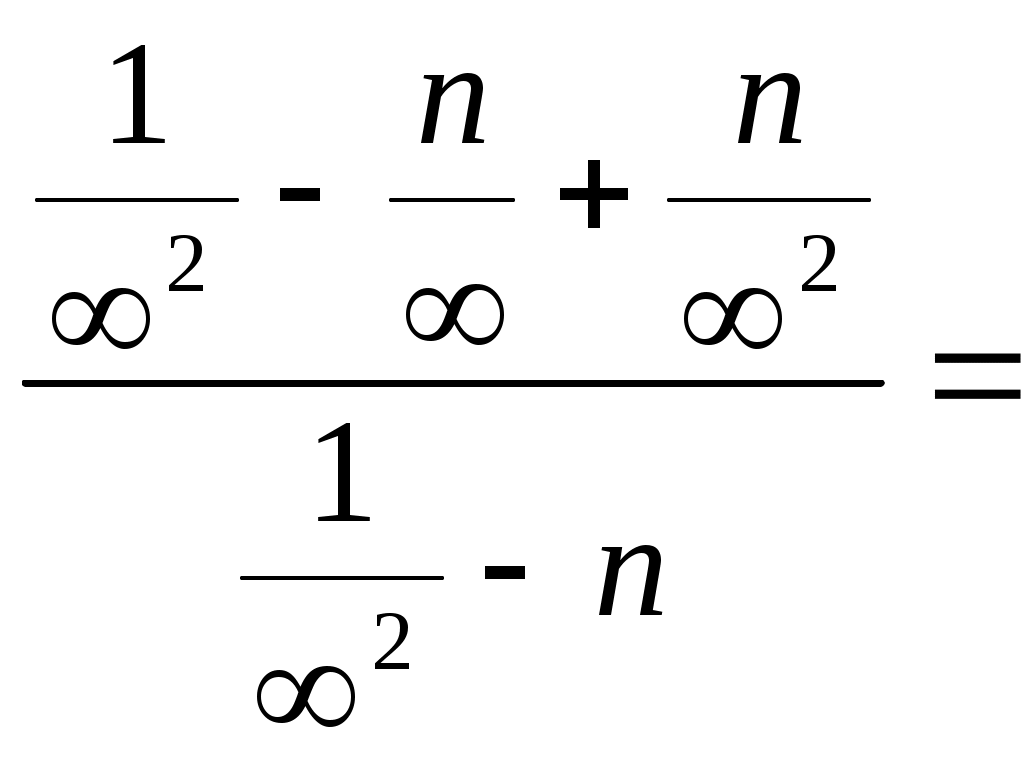
при k=2
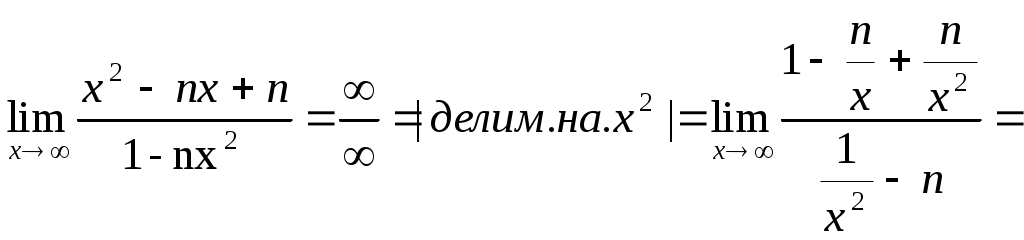
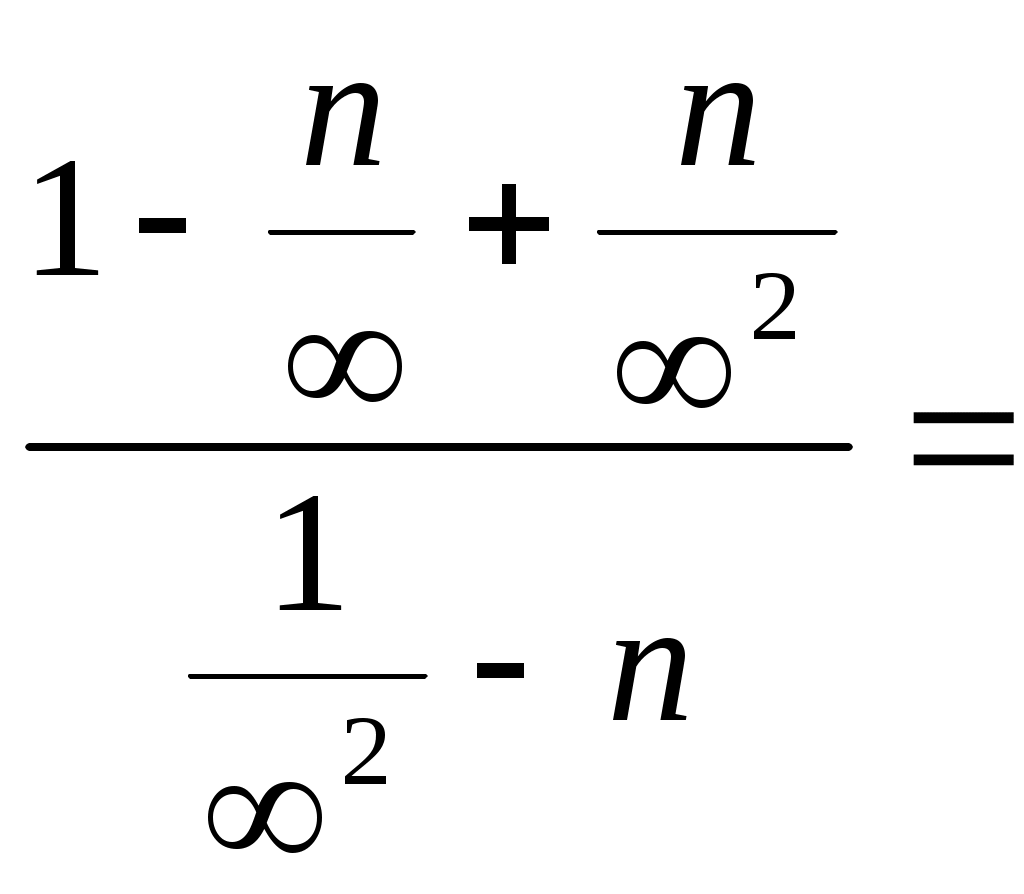
б)
в)
г)
Задача 8. Исследуйте функцию на непрерывность графически. Определите характер
точек разрыва с помощью односторонних пределов.
Варианты 1-15.
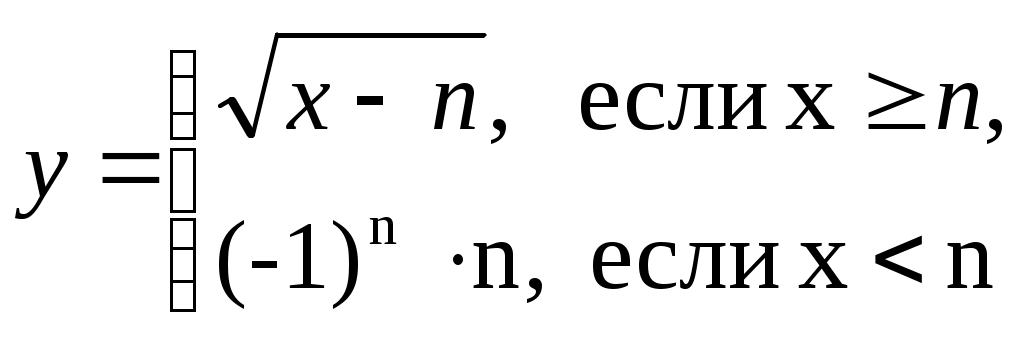
Решение
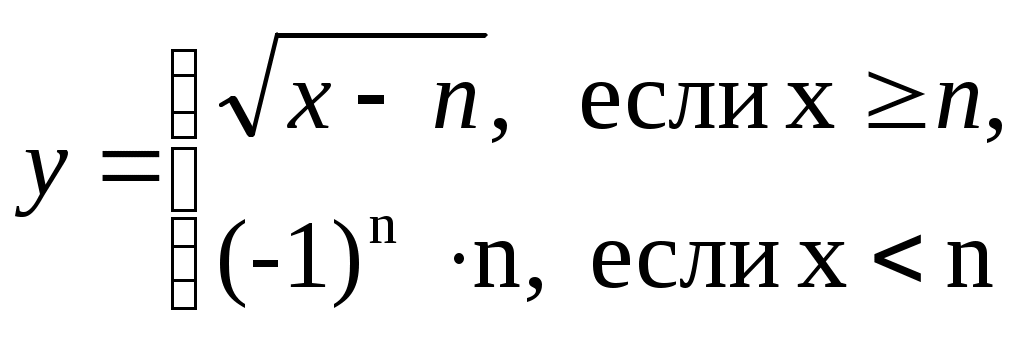

Односторонние пределы конечны и не равны, поэтому x=n=3 – точка разрыва 1 рода.
Задача9*. Запишите комплексное число в алгебраической, тригонометрической.
Варианты 1-15.
Решение
Алгебраическая форма:
Тригонометрическая форма:
z=1(cos(-90o)+isin(-90o)) z=cos90o - isin90o
Задача 10. Найдите производные и дифференциалы 1 порядка.
Варианты 1-5, 11-20. а) у = (n-2x)e n-x, б) y = ln
Решение
а) Применим правила дифференцирования произведения и сложной функции:
у / = (n-2x)/ e n-x + (n-2x) (e n-x ) / = -2 e n-x + (n-2x) e n-x (n-x)/ =
= -2 e n-x + (n-2x) e n-x (-1) =(2x-n-2) e n-x = (2x-5) e 3-x
dy=f /(x)dx= (2x-5) e 3-x dx
б) Применим правила дифференцирования частного и сложной функции:
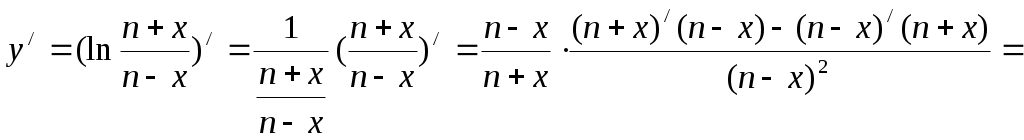
dy=f /(x)dx=
Задача 11. Найдите пределы по правилу Лопиталя:
Варианты 1-5 а)
Решение
а)
б)
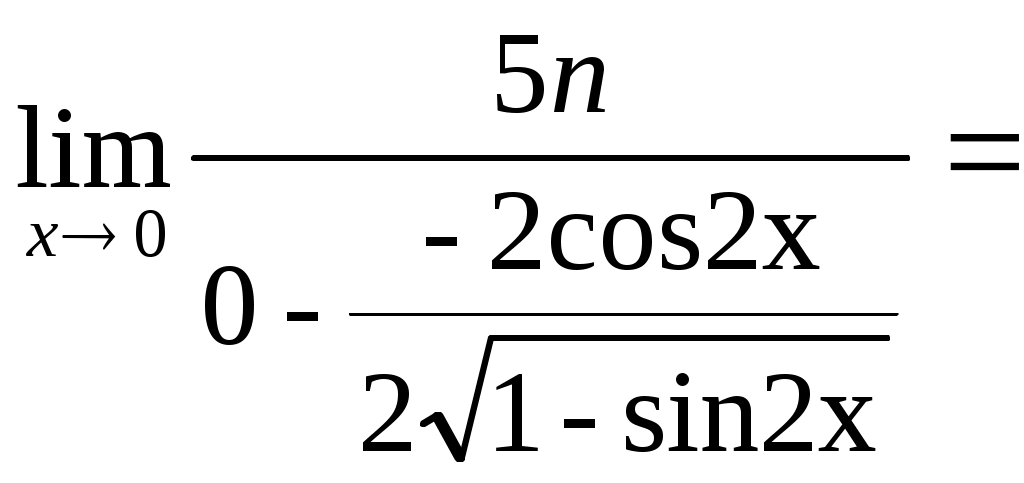
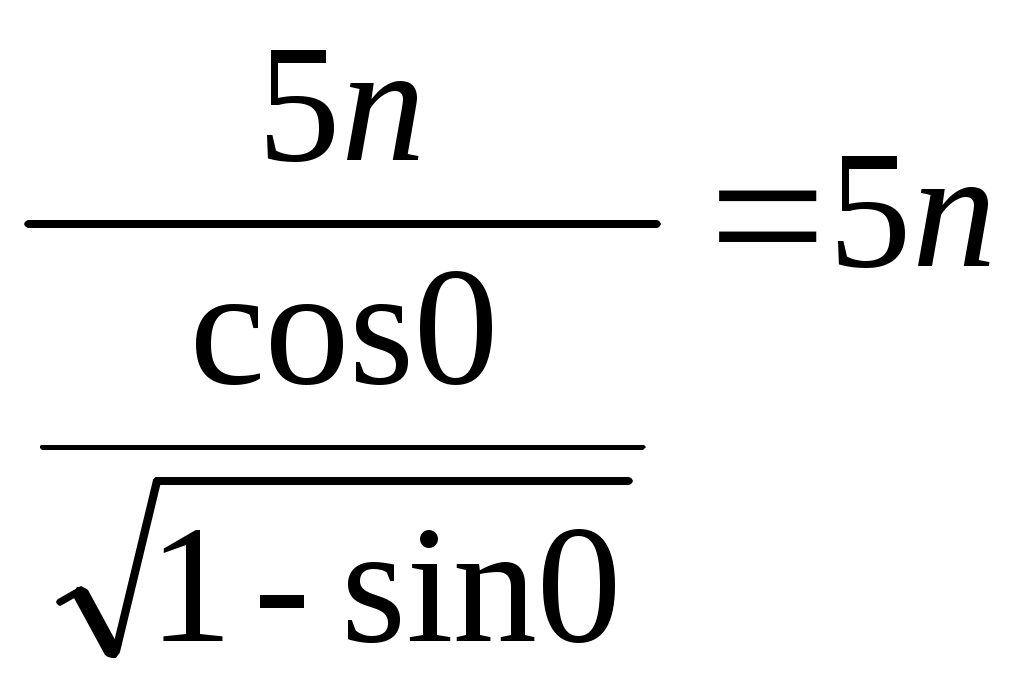 =15
=15 Задача 12. Найдите уравнение касательной к графику функции
Сделайте чертеж.
Решение
Сделаем чертеж

Уравнение касательной к графику функции y=f(x) в точке Mо(хо,уо) имеет вид:
у-f(xо)= f ’(xo)(х-хо).
f(xо)=
f ’(xo) =
Уравнение касательной:
у-1= 0,5(х-n) y=0,5x+1-0,5n = 0,5x-0,5
Задача 13. Найдите наибольшее и наименьшее значения функции
Решение
Найдем производную функции:
Производная не обращается в 0.
Производная не определена при x+1=0, откуда x=-1 – критическая точка вне отрезка [0,n].
Таким образом, наибольшее и наименьшее значения функции могут быть только на концах отрезка:
Наибольшее значение равно f(n)=0.
Наименьшее значение равно f(0)= -3.
СПИСОК ЛИТЕРАТУРЫ
-
Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление, М., 1988 -
Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов, ч.1, М.,1986 -
Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов: учебн. пособие для вузов. – М.: ЮНИТИ , 2004. – 474 с. -
Черненко В. Д. Высшая математика в примерах и задачах: учебное пособие для вузов. В 3 т.: Т. 1. – СПб.: Политехника, 2003. – 703 с.