М ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики


Практическая задание №2
по дисциплине «Информатика-2»

Вариант 9

Студент	О.Б.Харитонов (И.О. Фамилия)
Группа	ЭЭТбд-1801в
Преподаватель	Евгения Валерьевна Желнина

Тольятти 2023

Рассмотрим порядок выполнения задания на примере системы уравнений :

9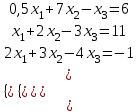

Технология выполнения задания в Microsoft Excel

1. 
   Для решения системы уравнений сформируем массивы коэффициентов системы уравнений (рис. 1):
   

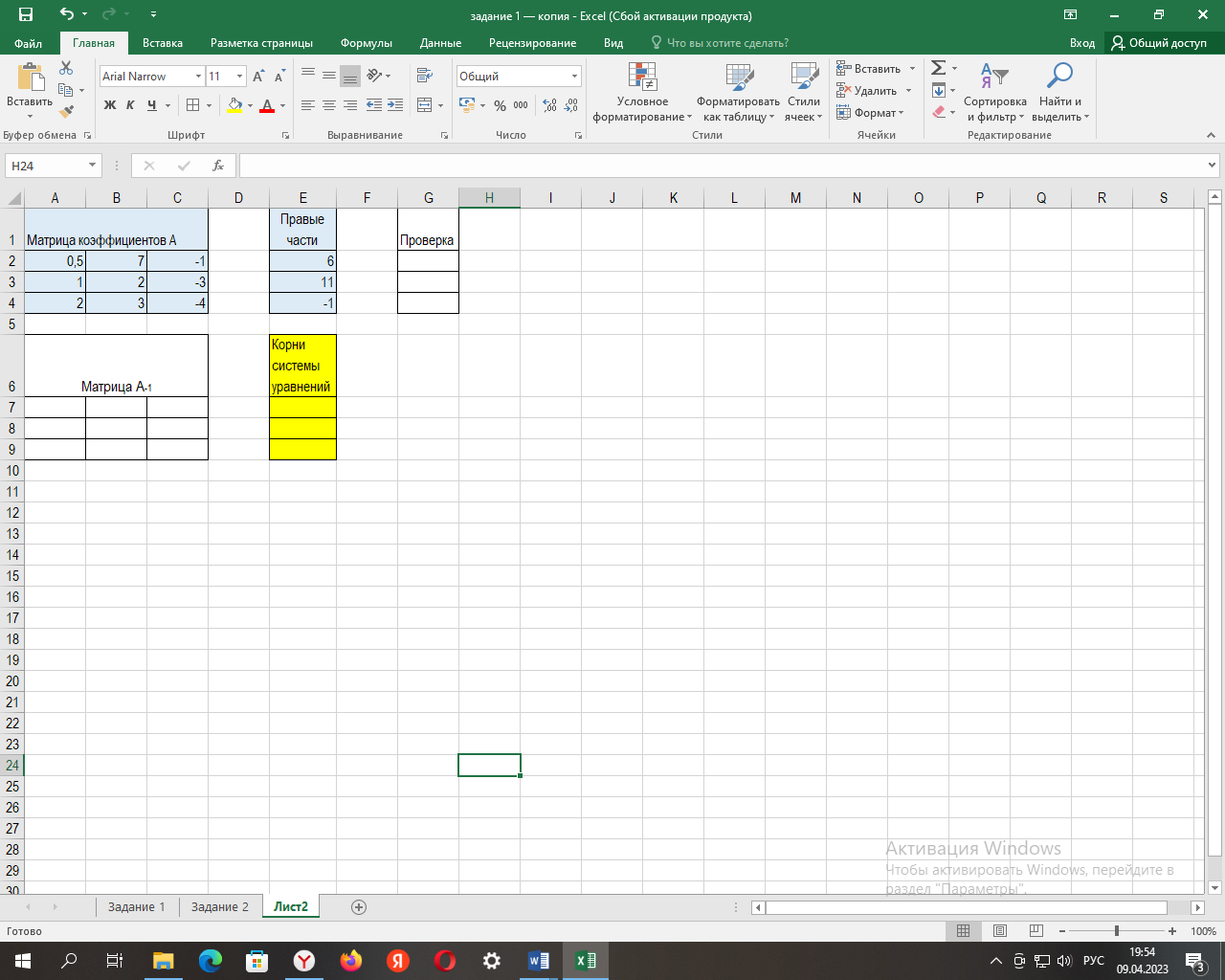
Рис. 1. Исходные данные для решения системы уравнений

2. 
   Для вычисления коэффициентов обратной матрицы А^-1 используем стандартную функцию МОБР. Для этого выполним ряд шагов:
   

• 
  выделим диапазон ячеек A7:C9, в котором будут находиться коэффициенты обратной матрицы;
  
• 
  выполним команды «Формулы – Математические – функция МОБР»;
  
• 
  в диалоговом окне (рис. 2) укажем в качестве аргумента функции диапазон ячеек А2:С4 (введем с клавиатуры или укажем мышью в таблице);
  
• 
  для закрытия окна функции МОБР используем комбинацию клавиш <Ctrl> + <Shift> + <Enter>, а не кнопку OK как обычно.
  

---

Формула вычисления обратной матрицы {=МОБР(А2:С4)} будет введена как формула массива в фигурных скобках (рис. 3). В результате применения формулы массива результат будет получен не в одной ячейке, а сразу в нескольких, в нашем случае в ячейках диапазона А7:С9.

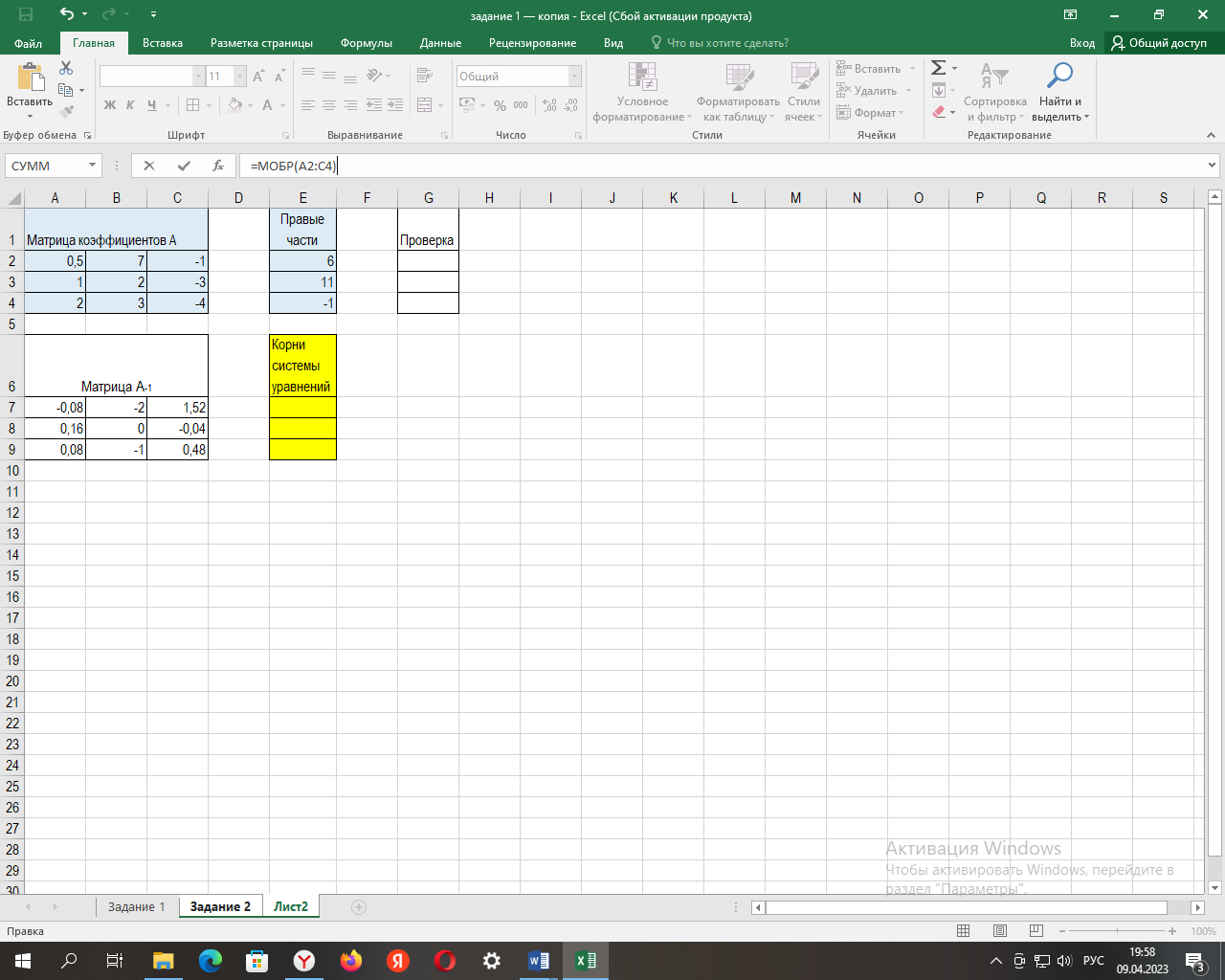
Рис. 3. Формирование обратной матрицы

3. 
   В ячейки диапазона E7:E9 введем как формулу массива формулу для вычисления корней системы уравнений: = МУМНОЖ(А7:С9;Е2:Е4) (рис. 4). В нашем случае получены корни системы уравнений (4): x1 =-24, x2 =1, x3 = -11.
   

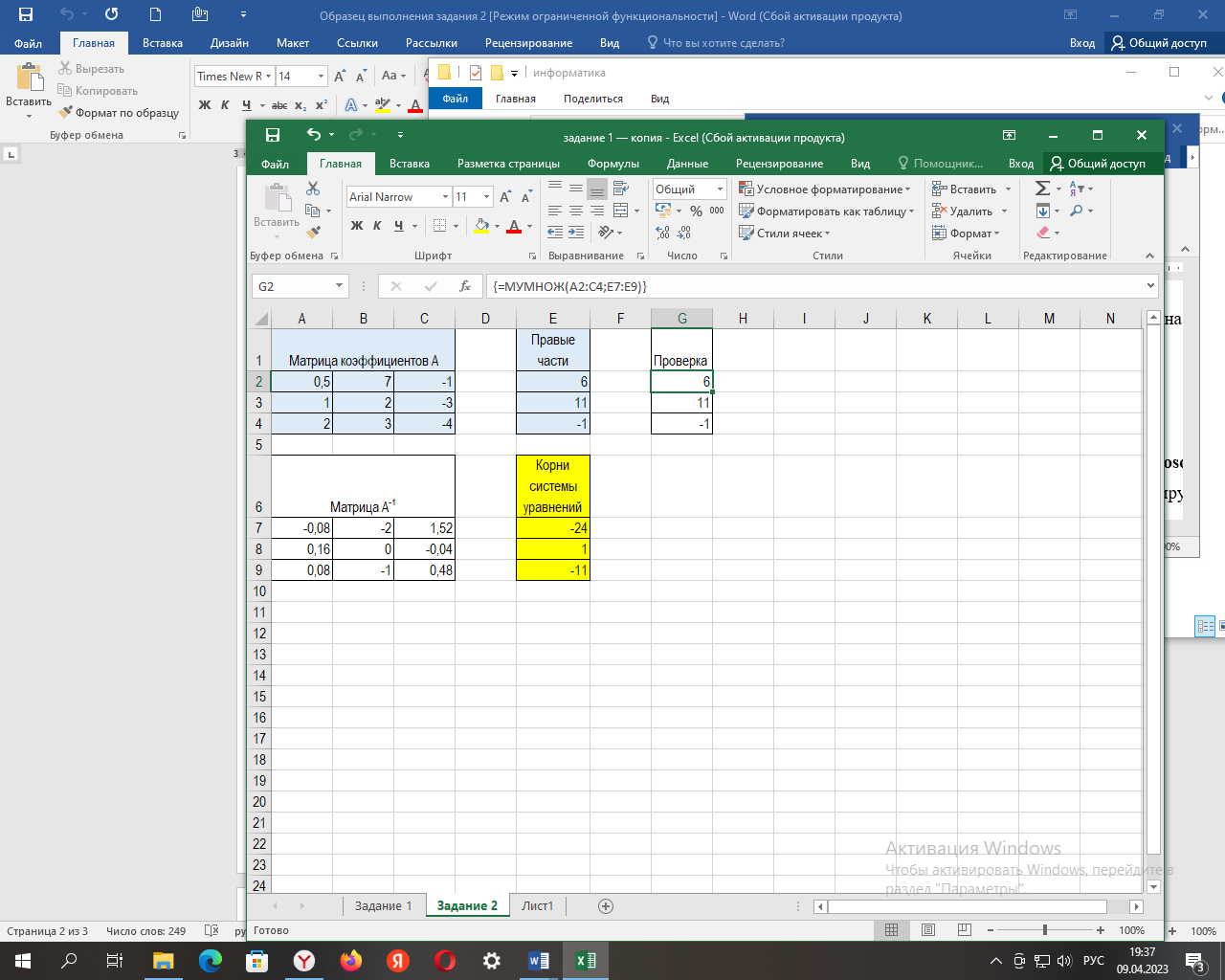
Рис. 4. Корни системы линейных уравнений и результат проверки правильности решения задачи

4. 
   Выполним проверку правильности решения задачи. Для этого в ячейках G2:G4 найдем произведение матрицы коэффициентов А (диапазон ячеек A2:C4) на вектор-столбец найденных корней системы уравнений (диапазон ячеек E7:E9) по формуле {= МУМНОЖ(A2:C4;E7:E9)}. В результате должен получиться вектор-столбец коэффициентов правых частей уравнений системы.
   

---

Смотрите также файлы

• "Административные правонарушения в сфере общественного порядка".rtf

• Народная фк.docx

• Ну, вот мы с вами и оказались в волшебном мире театра.(Включается аудиозапись первый театральный звонок).docx

• Теория менеджмента.docx

• Классный час к 1 сентября (6 класс) 20212022.doc