Файл: Решение Пусть событие а хотя бы одно попадание в волка из 4х выстрелов.docx

Сделать презентацию

Скачать файл (0,17Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.12.2023

Просмотров: 109

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

_{Задание}11. Из пяти карточек А, Б, В, Г, Д, наугад одна за другой выбираются 3 и располагаются в ряд в порядке появления. Какова вероятность того, что получится слово "два"?Решение:Всего имеется 5 букв, из них – одна буква " Д ", поэтому вероятность того, что первой будет буква " Д " равняется 1/5.Если первой была буква " Д " , то осталось 4 буквы, из которых одна буква "В", поэтому вероятность вынуть второй букву " В " равняется 1/4.Теперь букв на карточках осталось 3, из них 1 буква " А ", поэтому вероятность того, что третья буква – это буква " А " равняется 1/3.Тогда вероятность события А –" получится слово "два"" равняется: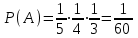Ответ: 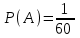.2. Два охотника стреляют в волка. Для первого охотника вероятность попадания в цель при одном выстреле равна 0,7, для второго – 0,8. Какова вероятность попадания в волка (хотя бы при одном выстреле), если охотники делают по два выстрела.Решение:Пусть событие А – «хотя бы одно попадание в волка из 4-х выстрелов»Противоположное событие 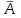– «ни одного попадания (четыре промаха)».Если для первого охотника вероятность попадания в цель при одном выстреле равна 0,7, для второго – 0,8, то вероятности промаха для первого охотника равна 0,3, для второго – 0,2.Тогда вероятность того, что будет четыре промаха: 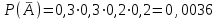.По теореме о вероятности противоположных событий: 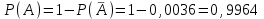, или 99,64%.Ответ: 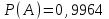, или 99,64%.3. В цехе работают 20 станков. Из них марки А – 10, марки В – 6, марки С – 4. Вероятность того, что качество детали окажется отличным, для этих станков соответственно равна – 0,9; 0,8; 0,7. Найти вероятность того, что взятая наудачу деталь окажется отличного качества.Решение:Используем формулу полной вероятности:

Если событие А происходит вместе с одной из событий Н₁, Н₂,…, Н_n, которые составляют полную группу попарно несовместимых событий, то события Н_к (к = 1, 2, …, n) называют гипотезами. Если известные вероятности гипотез и условные вероятности события А при выполнении каждой из гипотез, то вероятность события А в опыте S ( так называемая полная вероятность) исчисляется по формулеПусть событие А – наугад взятая из цеха деталь – отличного качества. Создадим три гипотезы:Н₁ – деталь изготовлена на станке марки А; Н₂ – деталь изготовлена на станке марки В;Н₃ – деталь изготовлена на станке марки С.По условию задачи 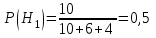; ;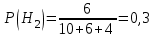 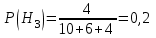.Вероятность того, что качество детали окажется отличным, для станков соответственно равна – 0,9; 0,8; 0,7, т.е. 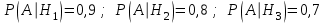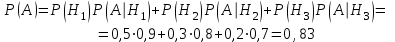условные вероятности отличного качества для каждого станка: .По формуле полной вероятности найдем вероятность того, что наугад взятая деталь - отличного качества:Ответ: 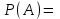0,83.4. На фабрике, изготовляющей болты, первая машина производит 25 %, вторая – 35 %, третья – 40 % всех изделий. В их продукции брак составляет соответственно 5 %, 4 %, 2 %. Случайно выбранный болт оказался дефектным. Какова вероятность того, что он сделан на третьей машине.Решение:Используем формулу полной вероятности:Пусть событие А – выбранный болт оказался дефектным. Создадим три гипотезы:Н₁ – болт изготовлен на первой машине; Н₂ – болт изготовлен на второй машине;Н₃ – болт изготовлен на третьей машине.По условию задачи

; ; .

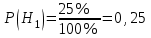
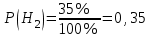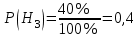Брак составляет соответственно 5 %, 4 %, 2 %., т.е. условные вероятности брака для каждой машины:

.

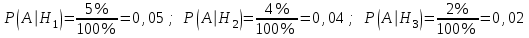По формуле полной вероятности найдем вероятность того, что случайно выбранный болт оказался дефектным:

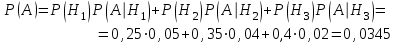
Используем формулу Байеса:

Если известно, что произошло событие А, и нужно найти вероятность того, что оно произошло именно с гипотезой Н_к, то есть условную вероятность гипотезы Н_к при условии А, то используется формула Байеса:

(к = 1, 2, …, n).

По формуле Байеса находим вероятность того, что бракованный болт сделан на третьей машине:

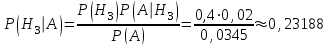
Ответ:
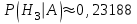
5. Вероятность того, что денежный автомат при опускании одной монеты сработает правильно, равна 0,97. Сколько нужно опустить монет, чтобы наивероятнейшее число случаев правильной работы автомата было 100?

Решение:

Наиболее вероятное число появлений события в схеме Бернулли находится по формуле:
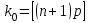– то есть целая часть числа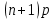

или из двойного неравенства:

.
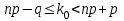Здесь событие А – правильное срабатывание автомата.

Вероятность р = 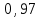, q = 1 – p = 1 – 0,97 = 0,03; 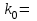100, n – ?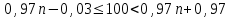

 

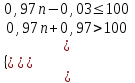
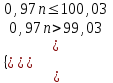
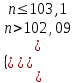  n = 103.
Ответ: n = 103, нужно опустить 103 монеты.

6. Вероятность появления события А в одном испытании равна p. Найти вероятность того, что в n независимых испытаниях событие

А произойдет: а) m раз; б) от k₁ до k₂раз. а) p = 0,17, n = 600, m = 90; б) n = 100, p = 0,85, 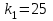, k₂ = 80.Решение:а) Если проводится n независимых испытаний, в каждом из которых событие А происходит с вероятностью р, то вероятность того, что событие А настанет ровно k раз, находится за формулой Бернулли, но при больших значениях n и k пользоваться формулой Бернулли неудобно из-за громоздкости вычислений. 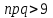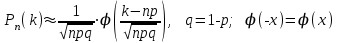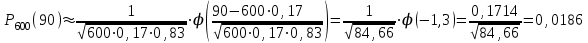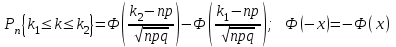В таких случаях при используем локальную теорему Муавра –Лапласа:р = 0,17 ; q = 1 – р = 1 – 0,17 = 0,83, n= 600, k = 90 :б) Используем интегральную теорему Муавра-Лапласа: Если проводится n независимых испытаний, в каждом из которых событие А происходит с вероятностью р, то вероятность того, что событие А настанет не меньше k₁ раз и не больше k₂ раз, равняется:Здесь n = 100; р = 0,85 ; q = 1 – р = 1 – 0,85 = 0,15 ; k₁= 25, k₂= 80.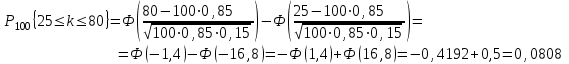Ответ: а) 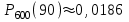; б) 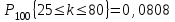.7. 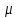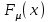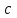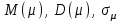Случайная величина задана функцией распределения .Требуется найти: а) постоянную ; б) плотность распределения вероятностей ; в)основные числовые характеристики 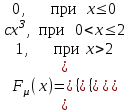;  = 0;  = 1.Решение:а) Функция распределения случайной величины 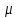непрерывная, поэтому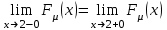

. Отсюда получаем 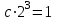 с= 1/8.

Итак, функция распределения имеет вид :

=
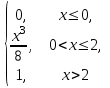
б) Плотность распределения 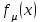является производной от функции распределения 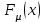, т.е. = .

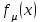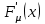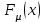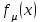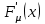При х ≤ 0 получаем: = 0  = = 0

При 0 < х ≤ 2 получаем: =  = =

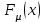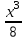
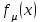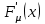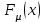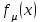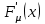При х > 2 имеем: = 1  = = 0 .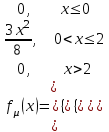

в) Вычислим числовые характеристики :

Для непрерывных случайных величин математическое ожидания (среднее значение) и дисперсия находится за формулами:

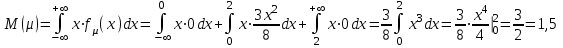
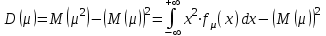
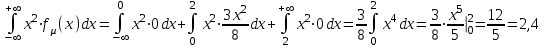
Тогда дисперсия: .
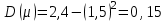Среднее квадратичное отклонение – это корень квадратный из дисперсии:

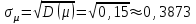
8. В таблице дано распределение 50 заводов по объёму валовой продукции (млн р.) и себестоимости