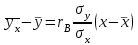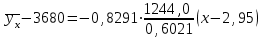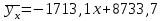Файл: Решение Пусть событие а хотя бы одно попадание в волка из 4х выстрелов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(р.).
Требуется: а) вычислить условные средние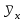
; б) вычислить выборочный коэффициент корреляции и проанализировать тесноту связи между признаками 
и 
;
в) составить выборочное уравнение прямой регрессии.
Решение:
а) Найдем средние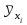
, то есть средние значения показателя (или у в обозначениях в заданной таблице) , вычисленные для каждого значения признака (или х) по формуле: 
.
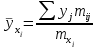Зависимость между значениями x и средними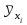 называется корреляционной зависимостью Y на Х . Ее можно записать с помощью таблицы:
б) Значения х і у в таблице заданы с равноотстоящими вариантами с шагом h1 = 0,5 для х і с шагом h2 = 1000 для у, поэтому для упрощения расчетов можно перейти к условным вариантам u и v по формулам:
,
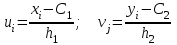где С1 и С2 – это такие значения х i у, которые стоят приблизительно в середине вариационного ряда и имеют самую большую частоту. В данном случае выбираем С1 = 3.0, С2 = 3500, тогда
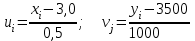
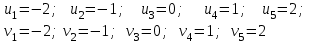
Получаем новую корреляционную таблицу:
Коэффициент корреляции rв рассчитываем по формуле :
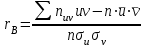, n = 50
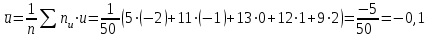
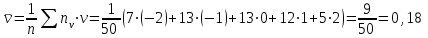
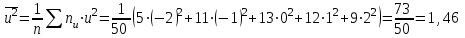
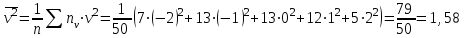
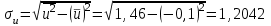
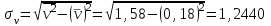
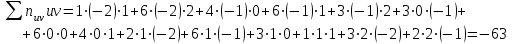
Тогда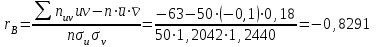
Получаем: 0 < |rв| <1, то есть Х і Υ – зависимые случайные величины, причем чем ближе |rв| к единице, тем ближе зависимость между Х і Υ к линейной зависимости. В экономических исследованиях при значениях коэффициента корреляции 0,7 – 0,9 связь считают тесной, если же значение коэффициента корреляции 0,2 – 0,4 связь считают слабой.
В данном случае r ≈ -0,83, теснота линейной связи между факторами Х i Y существенная, а так как величина отрицательная, то связь обратная.
По формулами моментов перейдем к вариантам Х и Y :
Уравнение регрессии Y на Х имеет вид: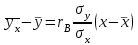
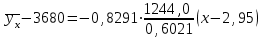
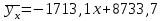
| x | y |  | |||||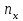
| 1500 | 2500 | 3500 | 4500 | 5500 | | ||
| 2,0 | | | | 1 | 6 | 7 | |
| 2,5 | | | 4 | 6 | 3 | 13 | |
| 3,0 | | 3 | 6 | 4 | | 13 | |
| 3,5 | 2 | 6 | 3 | 1 | | 12 | |
| 4,0 | 3 | 2 | | | | 5 | |
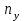 | 5 | 11 | 13 | 12 | 9 | 50 | |
Требуется: а) вычислить условные средние
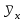; б) вычислить выборочный коэффициент корреляции и проанализировать тесноту связи между признаками и ; в) составить выборочное уравнение прямой регрессии.
Решение:
а) Найдем средние
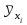, то есть средние значения показателя (или у в обозначениях в заданной таблице) , вычисленные для каждого значения признака (или х) по формуле: 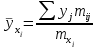.Зависимость между значениями x и средними
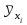называется корреляционной зависимостью Y на Х . Ее можно записать с помощью таблицы:| x | 2 | 2,5 | 3 | 3,5 | 4 |
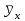 | 5357,14 | 4423,08 | 3576,92 | 2750,00 | 1900,00 |
| mx | 7 | 13 | 13 | 12 | 5 |
б) Значения х і у в таблице заданы с равноотстоящими вариантами с шагом h1 = 0,5 для х і с шагом h2 = 1000 для у, поэтому для упрощения расчетов можно перейти к условным вариантам u и v по формулам:
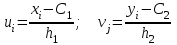,где С1 и С2 – это такие значения х i у, которые стоят приблизительно в середине вариационного ряда и имеют самую большую частоту. В данном случае выбираем С1 = 3.0, С2 = 3500, тогда
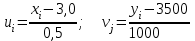
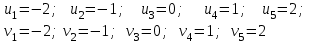
Получаем новую корреляционную таблицу:
| u v | -2 | -1 | 0 | 1 | 2 | nv |
| -2 | | | | 1 | 6 | 7 |
| -1 | | | 4 | 6 | 3 | 13 |
| 0 | | 3 | 6 | 4 | | 13 |
| 1 | 2 | 6 | 3 | 1 | | 12 |
| 2 | 3 | 2 | | | | 5 |
| nu | 5 | 11 | 13 | 12 | 9 | n = 50 |
Коэффициент корреляции rв рассчитываем по формуле :
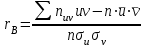, n = 50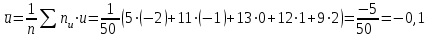
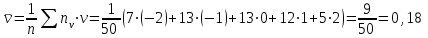
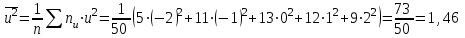
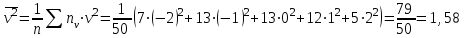
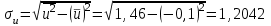
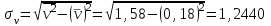
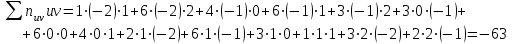
Тогда
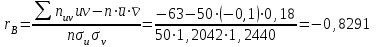
Получаем: 0 < |rв| <1, то есть Х і Υ – зависимые случайные величины, причем чем ближе |rв| к единице, тем ближе зависимость между Х і Υ к линейной зависимости. В экономических исследованиях при значениях коэффициента корреляции 0,7 – 0,9 связь считают тесной, если же значение коэффициента корреляции 0,2 – 0,4 связь считают слабой.
В данном случае r ≈ -0,83, теснота линейной связи между факторами Х i Y существенная, а так как величина отрицательная, то связь обратная.
По формулами моментов перейдем к вариантам Х и Y :
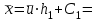 | -0,1 | 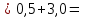 | 2,95 |
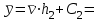 | 0,18 | 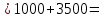 | 3680 |
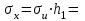 | 1,2042 | 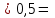 | 0,6021 |
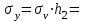 | 1,2440 | 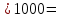 | 1244,0 |
Уравнение регрессии Y на Х имеет вид: