Файл: Высшая математика 2й семестр 202223 учебного года для потока иксс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 44
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Высшая математика 2-й семестр 2022-23 учебного года для потока ИКСС
Раздел РПД 5,6: Кратные и криволинейные интегралы
| Двойной интеграл. Определение и свойства. Двойной и повторный интегралы. Двойной интеграл в полярных координатах. Замена переменных. ВВМ4 стр. 3-21 ВВМ4* стр. 26-30 для продвинутых |
| Криволинейные интегралы первого и второго типов. Криволинейные интегралы первого типа. Криволинейные интегралы второго типа. ВВМ4 стр. 44-52 |
| Формула Грина. Условие независимости криволинейного интеграла от пути интегрирования; потенциальная функция. Формула Грина. Условие независимости криволинейного интеграла от пути интегрирования; потенциальная функция. ВВМ4 стр.52-55 |
Тестовые вопросы по разделам 5,6
-
Расставить пределы в двойном интеграле по области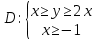 .
. -
Чему равен двойной интеграл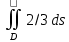 , если
, если 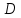 круг единичного радиуса?
круг единичного радиуса? -
Чему равен интеграл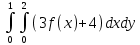 , если
, если 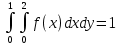 ?
? -
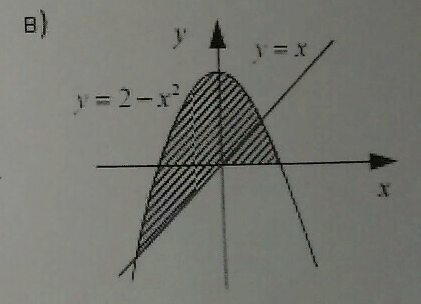
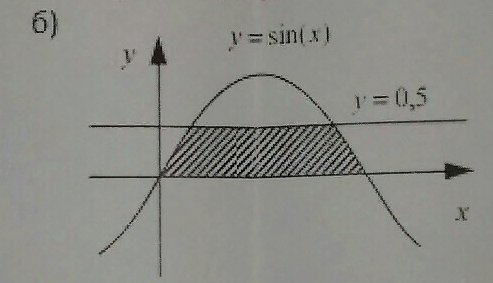
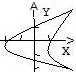 В каком порядке надо интегрировать, чтобы двойной интеграл по области, изображенной на рисунке сводился к одному повторному интегралу?
В каком порядке надо интегрировать, чтобы двойной интеграл по области, изображенной на рисунке сводился к одному повторному интегралу? -
В направлении какой оси область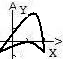 правильная?
правильная? -
Расставьте пределы интегрирования в повторном интеграле:
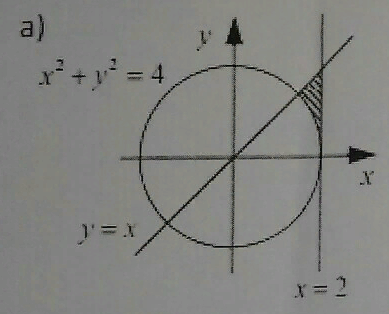
-
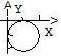 В каких пределах изменяется полярный угол
В каких пределах изменяется полярный угол 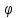 , если двойной интеграл вычисляется по области, изображенной на рисунке?
, если двойной интеграл вычисляется по области, изображенной на рисунке? -
Перейти к полярным координатам в интеграле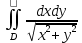 по области
по области 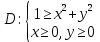 .
. -
Перейти к полярным координатам в интеграле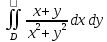 по области
по области 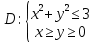 .
. -
Зависит ли криволинейный интеграл 2 рода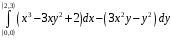 от пути интегрирования? Подтвердите свой вывод вычислением.
от пути интегрирования? Подтвердите свой вывод вычислением. -
Вычислить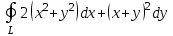 по формуле Грина, где L – контур треугольника с вершинами в точках A(1;1), B(2;2), C(1;3).
по формуле Грина, где L – контур треугольника с вершинами в точках A(1;1), B(2;2), C(1;3).
Раздел РПД 7: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
| Дифференциальные уравнения. Понятие дифференциального уравнения. Задача Коши, теорема существования и единственности, общее решение, общий интеграл. Уравнения с разделяющимися переменными. ВВМ3 стр.86-93, 98-105 |
| Линейные уравнения первого порядка. Решение методами Лагранжа и Бернулли. Уравнение Бернулли. Уравнения порядка выше первого. Уравнения, допускающие понижение порядка. ВВМ3 стр.105-111, 122-123* для продвинутых, 126-123 |
| Линейные уравнения второго порядка; теоремы об определителе Вронского, теоремы о структуре общего решения однородного и неоднородного уравнений. Метод вариации постоянных ВВМ3 стр.105-111, 122-123* для продвинутых, 132143 |
| Решение линейных однородных уравнений второго порядка с постоянными коэффициентами. Решение линейных уравнений второго порядка с постоянными коэффициентами и специальной правой частью. Метод подбора. ВВМ3 стр.143-146,152-157 |
Тестовые вопросы по разделу7
-
В каких точках не выполняются условия теоремы существования и единственности для ДУ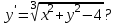
-
В каких точках не выполняются условия теоремы существования и единственности для ДУ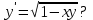
-
В каких точках не выполняются условия теоремы существования и единственности для ДУ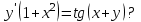
-
В каких точках не выполняются условия теоремы существования и единственности для ДУ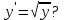
-
В каких точках не выполняются условия теоремы существования и единственности для ДУ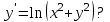
-
Является ли функция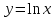 решением ДУ
решением ДУ 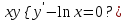
-
Является ли функция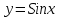 решением ДУ
решением ДУ 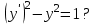
-
Является ли функция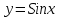 решением ДУ
решением ДУ 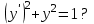
-
Является ли функция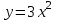 решением ДУ
решением ДУ 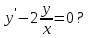
-
Общим решением какого ДУ является функция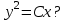
-
Общим решением какого ДУ является функция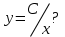
-
Общим решением какого ДУ является функция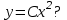
-
Общим решением какого ДУ является функция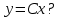
-
Является ли ДУ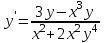 уравнением с разделяющимися переменными?
уравнением с разделяющимися переменными? -
Решением задачи Коши: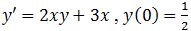 является функция
является функция 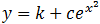
У
-
Решением задачи Коши:
является функция
-
Шарик на пружине смещают на 5см от положения равновесия и отпускают. Какие начальные условия нужно поставить для того, чтобы определить траекторию движения? -
Шарик на пружине проскакивает положение равновесия со скоростью 7см/сек Какие начальные условия нужно поставить для того, чтобы определить траекторию движения? -
Какие начальные условия нужно поставить, чтобы найти интегральную кривую ДУ 2-ого порядка, проходящую через точку (2,-3) параллельно прямой у=4х-5? -
Какие начальные условия нужно поставить, чтобы найти интегральную кривую ДУ 2-ого порядка, проходящую через начало координат под углом 45 градусов к оси ОХ? -
Какие начальные условия нужно поставить, чтобы найти интегральную кривую ДУ 2-ого порядка, в точке пересечения оси ОУ имеющую касательную у=0,3х-0,6? -
Какие начальные условия нужно поставить, чтобы найти интегральную кривую ДУ 2-ого порядка, касающуюся оси ОХ в точке х=1? -
Являются ли линейно независимыми функции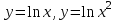 ?
? -
Являются ли линейно независимыми функции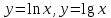 ?
? -
Являются ли линейно независимыми функции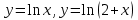 ?
? -
Является ли система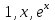 решений некоторого ОЛДУ 3го порядка линейно независимой?
решений некоторого ОЛДУ 3го порядка линейно независимой? -
Является ли система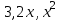 решений некоторого ОЛДУ 3го порядка линейно независимой?
решений некоторого ОЛДУ 3го порядка линейно независимой? -
Является ли система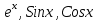 решений некоторого ОЛДУ 3го порядка линейно независимой?
решений некоторого ОЛДУ 3го порядка линейно независимой? -
Общим решением какого ОЛДУ является функция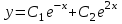 ?
? -
Общим решением какого ОЛДУ является функция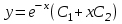 ?
? -
Общим решением какого ОЛДУ является функция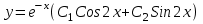 ?
? -
Общим решением какого ОЛДУ является функция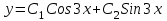 ?
? -
Общим решением какого ОЛДУ является функция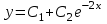 ?
? -
Найти вронскиан двух решений ОЛДУ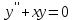
-
Найти вронскиан двух решений ОЛДУ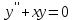
-
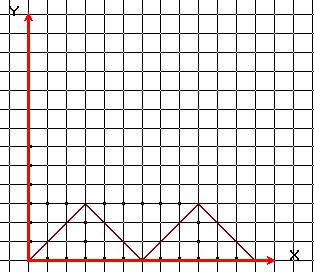
 Может ли график вронскиана, построенного на двух решениях ОЛДУ второго порядка иметь такой вид?
Может ли график вронскиана, построенного на двух решениях ОЛДУ второго порядка иметь такой вид? -
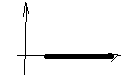 Может ли график вронскиана, построенного на двух решениях ОЛДУ второго порядка иметь такой вид?
Может ли график вронскиана, построенного на двух решениях ОЛДУ второго порядка иметь такой вид? -
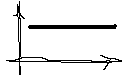 Может ли график вронскиана, построенного на двух решениях ОЛДУ второго порядка иметь такой вид?
Может ли график вронскиана, построенного на двух решениях ОЛДУ второго порядка иметь такой вид? -
Если у=1, у=lnx являются решениями ДУ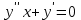 , то
, то 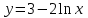 будет решением ДУ…?
будет решением ДУ…? -
Если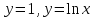 являются решениями ДУ
являются решениями ДУ 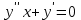 , то его общим решением будет …?
, то его общим решением будет …? -
Если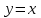 является решением ДУ
является решением ДУ 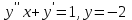 решением ДУ
решением ДУ 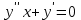 , то
, то 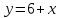 будет решением ДУ…?
будет решением ДУ…? -
Если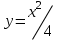 является решением ДУ
является решением ДУ 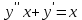 , то решением
, то решением 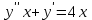 будет…?
будет…? -
Если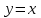 является решением ДУ
является решением ДУ 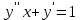 , то решением
, то решением 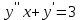 будет…?
будет…? -
Если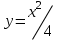 является решением ДУ
является решением ДУ 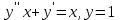 решением
решением 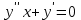 , то
, то 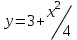 будет решением ДУ…?
будет решением ДУ…? -
Если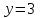 является решением ДУ
является решением ДУ 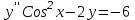 , то решением
, то решением 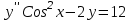 будет…?
будет…? -
Если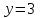 является решением ДУ
является решением ДУ 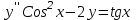 , то решением
, то решением 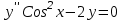 ,то
,то 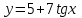 будет…?
будет…? -
Если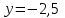 является решением ДУ
является решением ДУ 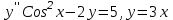 , то решением
, то решением 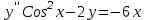 , то
, то 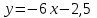 будет решением…?
будет решением…? -
Функция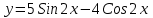 является решением ДУ
является решением ДУ 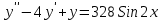 , а решением
, а решением 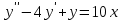 - функция
- функция 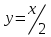 . Какая функция будет решением ДУ
. Какая функция будет решением ДУ 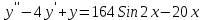 ?
? -
Функция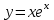 является решением ДУ
является решением ДУ 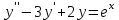 , а решением
, а решением 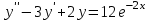 - функция
- функция 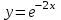 . Какая функция будет решением ДУ
. Какая функция будет решением ДУ 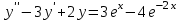 ?
? -
Можно ли понизить порядок дифференциального уравнения y’’+2xy’=1+y2
Если да – каким образом? К какому уравнению это приведёт?
-
Можно ли понизить порядок дифференциального уравнения (y’’)2+(y’)2=1? Если да – каким образом? К какому уравнению это приведёт? -
Составьте вид частного решения ЛНДУ2: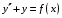 , если
, если 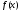 равна:
равна:
-
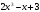 2)
2) 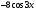 3) cosx 4)
3) cosx 4) 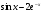 5)
5) 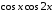
-
Составьте вид частного решения ЛНДУ2: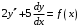 , если
, если 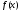 равна:
равна:
-
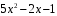 2)
2) 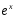 3)
3) 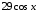
Раздел 8: ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
| Преобразование Лапласа. Изображения единицы, синуса и косинуса. Теоремы смещения, запаздывания, подобия, дифференцирования оригинала и изображения. Таблица оригиналов и изображений ВВМ4 стр.222-232 |
| Отыскание оригинала по изображению. Решение дифференциальных уравнений методом преобразования Лапласа. Теоремы о свёртке и об интегрировании оригинала. Формула Дюамеля. Решение интегральных уравнений методом преобразования Лапласа. ВВМ4 стр.232-234, 237-241 |
Тестовые вопросы по разделу 8
-
Является ли функция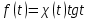 оригиналом?
оригиналом? -
Является ли функция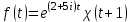 оригиналом?
оригиналом? -
Является ли функция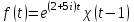 оригиналом?
оригиналом? -
Является ли функция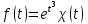 оригиналом?
оригиналом? -
Может ли функция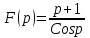 быть изображением?
быть изображением? -
Может ли функция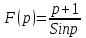 быть изображением?
быть изображением? -
Может ли функция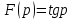 быть изображением?
быть изображением? -
Линейной комбинацией каких функций является оригинал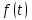 , если
, если 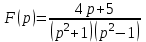 ?
? -
Линейной комбинацией каких функций является оригинал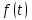 , если
, если 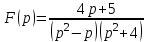 ?
? -
Линейной комбинацией каких функций является оригинал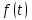 , если
, если 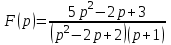 ?
? -
Линейной комбинацией каких функций является оригинал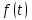 , если
, если 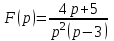 ?
? -
Линейной комбинацией каких функций является оригинал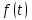 , если
, если 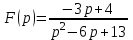 ?
? -
Линейной комбинацией каких функций является оригинал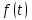 , если
, если 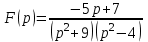 ?
? -
Линейной комбинацией каких функций является оригинал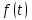 , если
, если 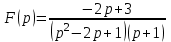 ?
? -
Найти изображение функции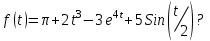
-
Найти изображение функции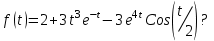
-
Найти изображение функции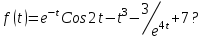
-
Найти изображение функции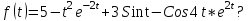
-
Найти изображение
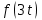 , если
, если 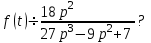
-
Найти изображение
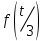 , если
, если 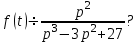
-
Найти изображение оригинала 1)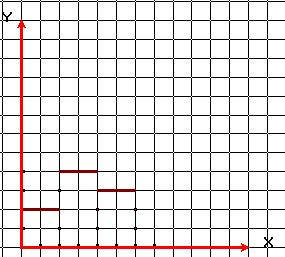 2)
2) 
-
Если
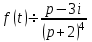 , то
, то 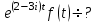
-
Если
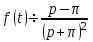 , то
, то 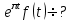
-
Если
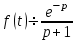 , то
, то 
-
Найти изображение
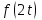 , если
, если 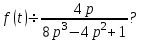
-
Найти изображение
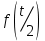 , если
, если 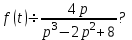
-
Найти изображение
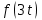 , если
, если 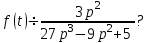
-
Если
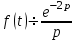 , то
, то 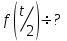
-
Если
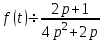 , то
, то 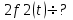
-
Найти изображение функции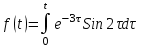
-
Найти изображение функции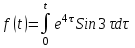
-
Найти изображение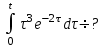
-
Найти изображение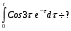
-
Найти изображение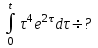
-
Найти изображение функции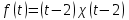
-
Найти изображение функции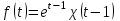
-
Найти изображение функции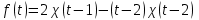
-
Найти оригинал функции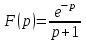
-
Найти оригинал функции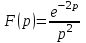
-
Найти оригинал функции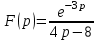
-
Найти оригинал функции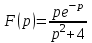
-
Найти оригинал функции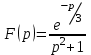
-
Если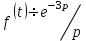 , то
, то 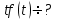
-
Если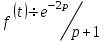 , то
, то 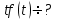
-
Найти изображение функции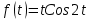
-
Найти изображение функции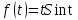
-
Найти изображение функции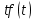 , если
, если 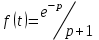
-
Найти изображение функции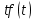 , если
, если 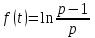
-
Найти изображение свертки функций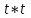
-
Найти изображение свертки функций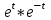
-
Найти изображение свертки функций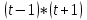
-
Найти изображение свертки функций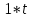
-
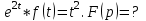
-
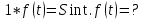
-