ФТБОУ ВПО НИЯУ МИФИ СарФТИ

Расчетно-проектировочная работа

«Исследование сложного напряженно-деформированного состояния в точке»

Выполнила:

студент группы ДП-20

Костин М. И.

Проверил:

Сырунин М. А.

2022

Краткая теория:

Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по трем взаимно перпендикулярным площадкам (сечениям), содержащим данную точку.



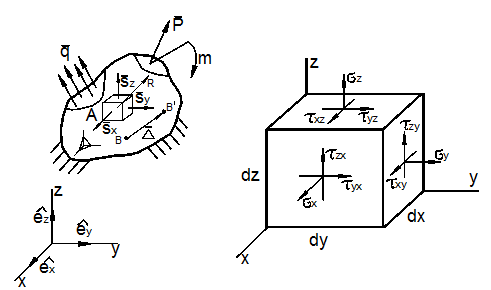
Действия отброшенной части тела заменим векторами – напряжениями   и разложим их на составляющие по координатным осям.



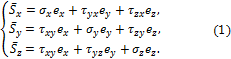
где e_x, e_y, e_z  - единичные векторы, направленные вдоль координатных осей x, y, z;  - нормальные напряжения,   - касательные напряжения. У касательных напряжений первый индекс указывает на направление его действия, второй индекс – на нормаль к площадке, на которой оно действует. Например,   — это касательное напряжение, действующее на площадке, перпендикулярной оси Х и направленное вдоль оси У. У нормальных напряжений индекс соответствует одновременно как направлению, так и нормали к площадке их действия. На невидимых на рис. 3.1 гранях частицы действуют такие же, но противоположно направленные напряжения.

Совокупность указанных напряжений полностью характеризует напряжённое состояние частицы тела. Эту совокупность записывают в виде квадратной матрицы

---

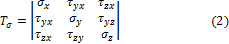
и называют тензором напряжений Коши. Система напряжений, приложенных к частице тела, должна удовлетворять условиям равновесия. Первые три условия в проекциях на оси x, y, z дают тождества, т.к. на противоположных гранях мы считаем напряжения равными по величине. Остаётся проверить, обращаются ли в нуль суммы моментов всех сил относительно координатных осей. Составим условие равновесия моментов относительно оси х:



откуда следует  _. Аналогично можно составить два уравнения равновесия моментов относительно осейy и z. В результате получим соотношения:



которые называют законом парности касательных напряжений: на двух взаимно перпендикулярных площадках составляющие касательных напряжений, ортогональные их общему ребру, равны по величине и направлены оба либо к ребру, либо от него. На основании этого закона тензор-матрица напряжений   является симметричной относительно главной диагонали, состоящей из нормальных напряжений.

Его можно разложить на сумму двух состояний – трёхосное растяжение и сложный сдвиг в трёх координатных плоскостях. На основании принципа независимости действия сил (напряжений), используя   , получаем:



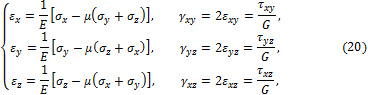
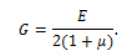
1. Закон упругого изменения объёма

Складывая в (20) относительные удлинения, получаем:



где 

---

 - относительное изменение объёма,   - модуль деформации.

2. Закон упругого формоизменения

Составим на основании (20), (23) выражение:



Аналогично можно найти разности  . В результате получаем соотношения



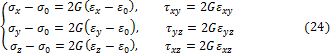
представляющие закон упругого формоизменения. Соотношения связывают компоненты девиаторов напряжений и деформаций.

3.Закон упругого упрочнения материала

Величину



называют модулем девиатором напряжений.

Теории прочности:

1.Первая теория прочности (Гипотеза наибольших нормальных напряжений).

Опасное состояние материала возникает, когда наибольшее по модулю нормальное напряжение достигает предельного значения соответствующего простому растяжению или сжатию.

Условие прочности:



где [σ_р] - допускаемое нормальное напряжение при одноосном растяжении; σ_с] - допускаемое нормальное напряжение при одноосном сжатии.

Эта теория дает удовлетворительные результаты лишь для некоторых хрупких материалов (бетона, камня, кирпича) и неприменима для пластичных материалов.

2.Вторая теория прочности (Гипотеза наибольших относительных удлинений).

В этой теории в качестве критерия разрушения принято наибольшее по модулю относительное удлинение ε.
Опасное состояние материала наступает тогда, когда наибольшее относительное удлинение достигает опасного значения.

Условие прочности:

---

где [σ] - допускаемое нормальное напряжение; µ - коэффициент Пуассона.

Экспериментально эта теория не подтверждается.

3.Третья теория прочности (Гипотеза наибольших касательных напряжений) или теория прочности Треска — Сен-Венана.

Причиной разрушения материала считается сдвиг, вызываемый касательными напряжениями. Полагают, что материал разрушается, когда наибольшее касательное напряжение достигает значения, предельного для данного материала.

Условие прочности:



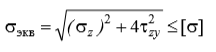
Теория подтверждается для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию.

4.Четвёртая теория прочности (энергетическая теория прочности).

Э 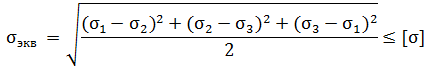та теория предполагает, что пластичный материал находится в опасном состоянии, когда удельная потенциальная энергия формоизменения достигает предельного для данного материала значения.

Условие прочности:
Теория подтверждается для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию.

5. Теория прочности Мора (пятая гипотеза прочности).

Т еория прочности Мора позволяет учесть различное сопротивление материалов растяжению и сжатию.
Например, бетон, который имеет высокую прочность на сжатие, но совершенно не может работать на растяжение.

Условие прочности:
При [σ_р] = [σ_с] теория прочности Мора совпадает с третьей теорией прочности.

---

---

Смотрите также файлы

• Методические указания по выполнению курсовой работы по дисциплине мдк 03. 02. Монтаж, наладка и эксплуатация электрических сетей.docx

• Презентация по выполнению кейсзадания по дисциплине Введение в профессиональную деятельность (Менеджмент). Семинар 2 Выполнил студент Стукман Артем Евгеньевич 1 курс.doc

• Нормативноправовая база 2.docx

• Ответы на вопросы по археологии.docx

• Вид вооружения, который советские войска впервые использовали в Смоленском сражении.doc