Добавлен: 06.12.2023
Просмотров: 36
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Государственное бюджетное общеобразовательное учреждение
Самарской области средняя общеобразовательная школа «Образовательный центр» имени Героя Советского Союза В.В. Субботина пос. Серноводск муниципального района Сергиевский Самарской области
(ГБОУ СОШ «ОЦ» пос. Серноводск)
ИТОГОВЫЙ ИНДИВИДУАЛЬНЫЙ ОБРАЗОВАТЕЛЬНЫЙ ПРОЕКТ
научно – исследовательский проект
Длина окружности и площадь круга. Применение формул при решении практико-ориентированных задач
предметная область: математика
Выполнила: Зайцева Виктория
ученица 8б класса
Руководитель: Давыдова Александра
Алексеевна
Серноводск, 2023 год
Содержание
Введение……………………………………………………………………………...3
Глава 1. Теоретические сведения по теме «Длина окружности. Площадь круга»…………………………………………………………………………………5
1.1.Длина окружности………………………………………………………………5
1.2. Площадь круга………………………………………………………………….9
Глава 2. Практическое применение формул длины окружности и площадь круга в окружающей действительности………………………………………………...12
2.1. Окружность и круг в достопримечательности городов……………………..12
2.2. Окружность и круг в природе…………….…………………………………..16
Заключение…………………………………………………………………………19
Список использованной литературы……………………………………………...20
Введение
Данная тема представляет определенный интерес, поскольку её истоки относятся к древности: с давних пор люди пытались решать задачи, связанные с кругом – измерять длину окружности, находить площадь круга.
Любой школьник сегодня должен уметь находить длину окружности и площадь круга, первый опыт вычислений происходит в 6 классе. Но, к сожалению, эти знания остаются для многих формальными, и уже через год мало кто помнит не только то, что отношение длины окружности к её диаметру одно и то число, но даже с трудом вспоминают численное значение числа π, равное 3,14.
Круг и окружность – одни из самых древнейших геометрических фигур, философы древности придавали им большое значение. Круг – воплощение нескончаемого Времени и Пространства, символ всего сущего, Вселенной. «Из всех фигур прекраснейшая – круг», – считал Пифагор.
Вокруг нас много круглых предметов. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезло все круглое! Казалось бы – пусть все будет квадратным. Разве нельзя прожить без круглых труб, а к квадратным колесам нельзя привыкнуть? Можно ли вообще представить жизнь человека без использования круга? Почему так много тел имеют круглую форму? Чтобы найти ответы на все эти вопросы, в первую очередь, необходимо рассмотреть историю возникновения этих понятий и дальнейшее их развитие.
Цель исследования: изучить теоретические сведения по теме «Длина окружности. Площадь круга» и представить примеры и иллюстрации применения данной теории в решении практико-ориентированных задач, сюжетных задач.
Для реализации данной цели необходимо решить следующие задачи:
-
Изучить теоретические сведения о круге и окружности; -
Исследовать изменение длины окружности и площади круга в зависимости от изменения длины радиуса; -
Рассмотреть занимательные задачи и практические ситуации, где необходимо применить данную теорию в решении профессиональных и иных проблем; -
Рассмотреть значимость теории в прикладных задачах, а также смежных областях науки и техники, где применяется теория по рассматриваемой теме.
Объект исследования: формулы длины окружности и площади круга.
Предмет исследования: задачи на применение формул длины окружности и площади круга.
Гипотеза исследования: сюжетные иллюстрации, решение задач практического содержания позволят обучающимся воспринимать тему «Длина окружности. Площадь круга» как необходимый и осмысленный инструмент для применения к решению задач определенной области. Многообразие форм представления данной теории позволит усвоить необходимый материал и поможет решить многие геометрические задания с похожим содержанием.
Мы считаем, что формирование навыков решения сюжетных, практических заданий по рассматриваемой теме позволит осмыслить важность прописанной теории и приведет к пониманию через осмысление принадлежности формул к конкретному условию.
Глава 1. Теоретические сведения по теме «Длина окружности. Площадь круга»
-
Длина окружности
Для построения окружностей имеется специальный инструмент – циркуль.
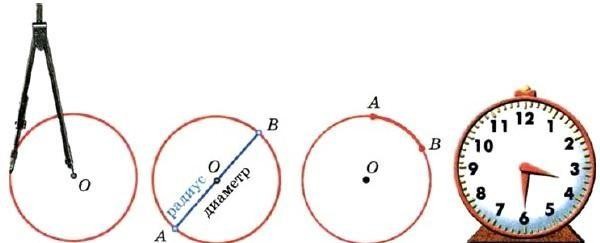
Рис. 1. Построение окружности с помощью циркуля.
Обратим внимание на то, что при проведении окружности точка В все время находится на одном и том же расстоянии от точки О, называемой центром окружности, а отрезок ОА называется радиусом окружности. Следовательно, окружность – это замкнутая кривая линия, все точки которой находятся на одном и том же расстоянии от ее центра.
Окружностью называется фигура, которая состоит из всех точек плоскости, находящихся на данном расстоянии от данной точки. Эта точка называется центром окружности.
Расстояние от точек окружности до ее центра называется радиусом окружности. Радиус окружности – это отрезок, соединяющий центр окружности с любой точкой на окружности. Хорда – это отрезок, соединяющий любые две точки на окружности. Самая большая хорда в окружности – диаметр, который так же можно представить в виде суммы двух радиусов.
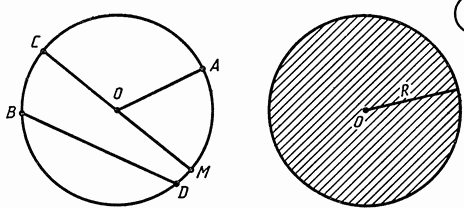
Рис. 2. Элементы окружности. Круг.
Часть плоскости, которая ограничивается окружностью, называется кругом.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
Можно сделать следующий вывод. Разница между кругом и окружностью заключается в следующем:
1. Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
2. Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
Впервые понятие длины окружности даётся в учебнике математика 6 класса.
«Возьмём круглый стакан, поставим на лист бумаги и обведём его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить её, то длина нитки будет приближённо равна длине нарисованной окружности». Есть несколько способов непосредственного измерения длины окружности.
1. Вырежьте из картона, фанеры или другого материала круг, поставьте его ребром на лист бумаги, где начерчена прямая линия. Отметьте на прямой и на окружности точку их касания А. Затем плавно катите круг по прямой до тех пор, пока отмеченная точка А на окружности не окажется на прямой в точке В. Отрезок АВ тогда будет равен длине окружности. Измерив его с помощью избранной единицы длины, мы тем самым измерим и длину окружности.
2. Оберните вырезанный из картона (фанеры или другого материала) круг веревочкой по окружности так, чтобы конец веревочки совпал с началом в одной и той же точке окружности. Затем растяните эту веревочку и измерьте ее длину. Длина веревочки будет равна длине окружности.

Рис. 3. Измерение длины окружности.
Однако эти способы непосредственного измерения длины окружности мало удобные и дают они приближенные результаты измерения.
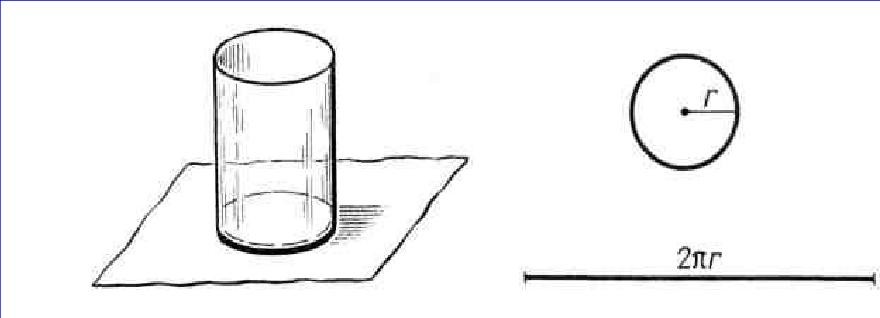
Рис. 4. Измерение длины окружности.
Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость.
Многие математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности, и найти более точное значение этого отношения. Впервые это удалось сделать древнегреческому математику Архимеду. Архимед установил, что отношение длины окружности к диаметру есть величина постоянная, и нашел довольно точное значение этого отношения. Это отношение стали обозначать греческой буквой π. Число приблизительно равно 3.14.
Обозначим длину окружности буквой L, а ее диаметр буквой d и выведем, чему равна длина окружности, если известен ее диаметр: L = π*d.
Если известен радиус R , то формула длины окружности будет выглядеть так: L = 2 πR.
Радиус окружности
Радиус окружности - это отрезок, соединяющий центр с какой- либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Определить радиус окружности можно по формуле: R= L /2 π.
Диаметр окружности
Хорда - отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Центр окружности является серединой любого диаметра. Определить диаметр окружности можно по формуле: D= L / ????.
1.2. Площадь круга
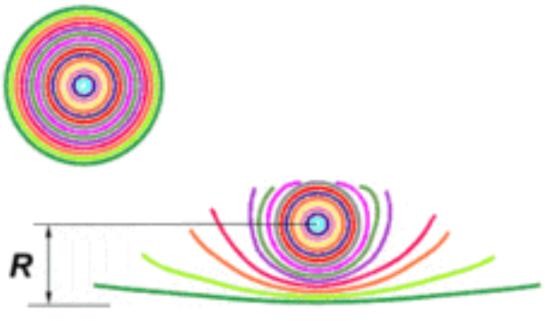
Рассмотрим круг и представим его как бесчисленное множество колец, смещающихся в центр. Для наглядности каждое кольцо представим в цветовой гамме. Перед нами представлен круг, состоящий из множества колец, со смещающимся радиусом к центру.
Рис.5. Круг, представленный в виде колец, смещающихся в центр.
Обозначим радиус этого круга, как показано на рисунке. Развернем каждую из окружностей, входящих в состав круга в свою длину.