Добавлен: 06.12.2023
Просмотров: 37
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 6. Преобразование круга в пирамиду.
Так как окружности к центру имеют меньший радиус, то множество развернутых окружностей образуют пирамиду. Обозначим длину развернутой окружности L. Каждую окружности своей длины разделим на две одинаковые части и обозначим каждую длину части как L/2.
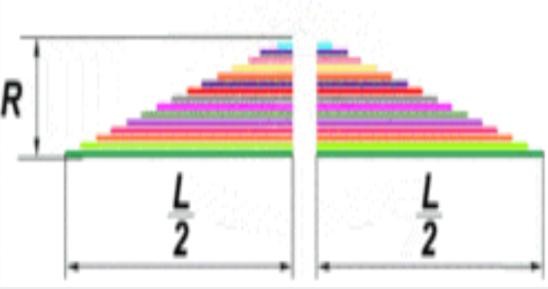
Рис. 7. Разделение пирамиды на две равные части.
Одну из частей пирамиды, которая образовалась в результате деления, перевернем, а в другой части смесим все доли (части) влево, как показано на рисунке. Видим, что в составе некоторых изменений, детали выставились зеркально относительно друг друга со смещением. Получились две детали одного целого прямоугольника, если их соединить.
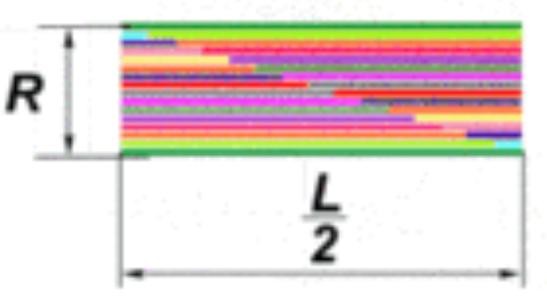
Рис. 8. Преобразование пирамиды в прямоугольник.
Соединив две части, получим известную всем фигуру прямоугольник, у которого обозначена ширина и длина. Можем перейти к нахождению площади прямоугольника.
Таким образом, не выбрасывая ни одного звена, у нас получилась фигура, разная по форме, но одинаковая по площади. Зная, что ???? = 2????????, ???? = ???? · 2???????? = ???? · ???? * ???? = ????????². Получилась формула для нахождения площади круга.
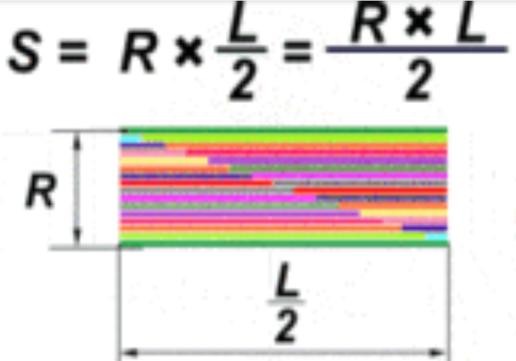
Рис. 9. Нахождение площади прямоугольника.
Глава 2. Практическое применение формул длины окружности и площадь круга в окружающей действительности
2.1. Окружность и круг в достопримечательности городов
Первым примером применения окружности в строительстве стали каменные сооружения эпохи первобытного строя. Да, ещё в первобытные времена геометрия стала проявляться в архитектуре. Самая известная постройка того времени - Кромлех в Стоунхендже (Англия). Заметим, что все колонны Стоунхенджа, когда-то были расположены строго по окружности.
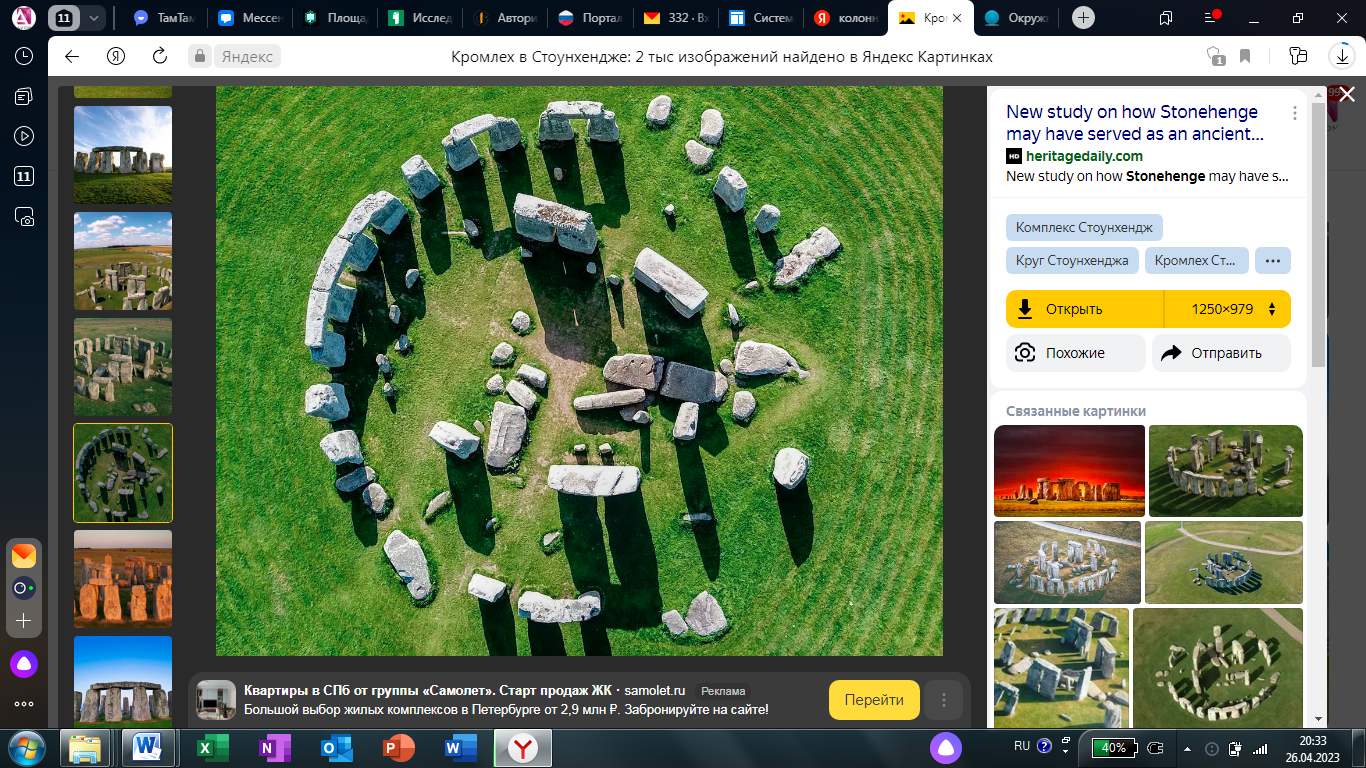
Рис.10.
Кромлех в Стоунхендже.
Так же существует легенда о вавилонской башне. Башня, которая должна была дотянуться до богов, но была уничтожена. Многие считают, что её разрушили сами боги, другие, что Вавилон всё это выдумал для устрашения врагов. Мне кажется, что в те времена науке отдавали мало времени, не было измерительных приборов, поэтому она разрушилась по вине зодчих.
Знаменитый Колизей в Риме имел стены, которые располагались по кольцам. Это здание сохранилось до нас. А сохранилось оно потому, что римский Император собрал лучших зодчих со всего мира, купил лучшие инструменты, хорошие каменные плиты и создал первый макет здания. Конечно, здание сильно разрушено, но с его постройки прошло ни одно тысячелетие. Ну и конечно средневековые замки, чьи городские башни имели округлую форму. В средневековье зодчеству и геометрии отдавали много времени - это стало необходимом в связи постоянных войн между феодалами. Башни в крепостях нужны были для размещения лёгкой пехоты (лучников), там их не могли достать вражеские стрелы, а при осаде лучники удерживали тараны и осадные башни.
Рассмотрим достопримечательности различных городов, где окружность и круг применяются в качестве основы проекта. Город Самара является одним из таких городов. Округлые формы придают сооружениям нашего города особый вид и красоту.
Площадь революции впервые появилась на плане города в 1782 году и предназначалась для торговли. В 1889 состоялось открытие работы архитектора В. Шервуда в центре круглого сквера памятнику Александру II диаметром 38 метров. Царь изображен в шинели, у подножия памятника четыре фигуры олицетворяли четыре исторических события: освобождение крестьян от крепостничества, покорение Кавказа, освобождение болгар от турецкого ига, завоевание Средней Азии. Пьедестал выполнен из красного финского гранита. В 1918 году скульптура царя и все его бронзовые детали были уничтожены. Площадь стала называться площадью Революции. 7 ноября 1927 года на уцелевшем пьедестале была установлена фигура Ленина.
Задача 1. Найдите площадь круга, зная, что диаметр площади Революции составляет 38м.
Решение: ???? = 38 m
???? = ???? : 2 = 19 m
???? = 3,14
???? = ????*????2 = 3,14 * 19
* 19 = 1133,54 m2
Ответ: 1133,54 m2
Задача 2. Конструкция сферической оболочки стадиона «Самара-Арена» состоит из 32 стальных консолей, каждая из которых весит по 277 тонн. Вместе они создают купол диаметром 612 метров. Найдите длину купола, ответ округлите до целых.
Решение: ???? = 612м
L = ???? * ???? = 3,14 * 612 = 1921,68м ≈ 1922м.
Ответ: 1922м.
Задача 3. Длина кольца «Самолёт» на Московском шоссе составляет 333 м. Найдите диаметр окружности и площадь построения. Диаметр и площадь округлите до целых.
Решение: 1) Найдем диаметр построения:
L = 333м
L = ???????? = 333м
???? = 3,14
3,14 · ???? = 333м
???? = 333:3,14 ≈106,051≈ 106м
???? = ???? ÷ 2 ≈ 53м
2) Найдем площадь построения: ???? = ????*????² = 3,14 · 53 · 53 = 8820,26 ≈ 8820м²
Ответ: 106м, 8820м².
Круглые дома в Москве - жилые панельные девятиэтажные дома кольцевой формы, возведённые на западе Москвы в 1970-х годах по экспериментальному проекту советского архитектора Евгения Стамо и инженера Александра Маркелова. Здания диаметром в 155 метров были
построены из типовых деталей панельной серии I-515/9M.

Рис.11. Круглый дом в Москве.
Задача 4. Найти площадь круглого дома в Москве.
Решение: Обратимся к карте для поиска необходимых данных.
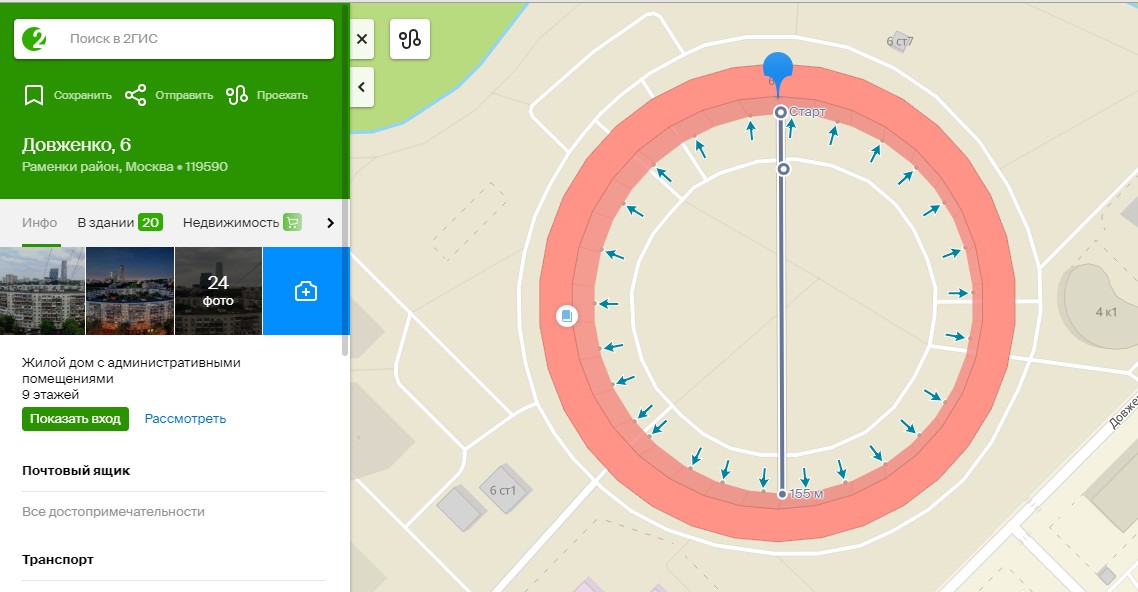
Рис.12. Работа с картой.
Замер на карте: диаметр всего круга равен 193 метра, диаметр двора – 155 метров. Чтобы найти диаметр постройки, необходимо найти площадь двора и вычесть ее от общей площади, занятой двором и домом вместе. Пусть ????1 = 193 : 2 = 96,5 метров – радиус общей постройки, тогда ????2 = 153:2 = 77,5 метров – радиус двора.
???? = ????*????12 - ????*????22 = 3,14 * 96,5 * 96,5 – 3,14 * 77,5 * 77,5 = 29240,465 – 18859,625 = 10380,84 ≈ 10381м²
Ответ: 10381м².
2.2. Окружность и круг в природе.
Несомненно, достопримечательностью городов являются не только строительные сооружения, придуманные человеком. Человек мог бы не обратить внимание на такую геометрическую фигуру как круг или окружность, если бы не встретил ее в природе. Рассмотрим несколько задач, связывающих окружность и круг с природой.
Недалеко от Пензы находится озеро, которое местные жители называют Мертвым. Там совершенно нет жизни, но это не самая главная его особенность. Дело в том, что Мертвое озеро представляет собой идеальный круг. Кажется, что окружность диаметром 450 метров начертили гигантским циркулем. При этом ученые говорят, что человек здесь ни при чем, просто так сложилось в природе.

Рис. 13. Мертвое озеро в Пензенской области.
Задача 5. Найти площадь Мертвого озера, если его диаметр равен 450 метров.
Решение: Радиус озера – 450 : 2 = 225 метров. ???? = ????*????2 = 3,14 * 225 * 225 = 158962,5 ≈ 158963 м²
Ответ: 158963 м².
Существует интересный подвид секвой – дендроны, отличающиеся меньшей высотой, но большим диаметром стволов. Самая объёмная секвойя в мире относится именно к этому подвиду, это 83,8-метровый "Генерал Шерман".

Рис.14. Секвойя Генерал Шерман.
Задача 6. Найти диаметр секвойи, если ее обхват составляет 34,9 метров.
Решение: L = ???????? = 34,9м
???? = 34,9 : 3,14 ≈ 11,11м
Ответ: 11,11м
В Сергиевском районе Самарской области находится удивительное Голубое озеро, его форма тоже напоминает нам окружность. Озеро сероводородное, образовалось в карстовой воронке глубиной около 40 метров и свое название получило за интенсивную изумрудно-голубую окраску воды. Озеро прекрасно в любое время суток и время года.
Задача 7. Найти площадь Голубого озера, если его диаметр составляет около 42 метров.
Решение: Радиус озера – 42 : 2 = 21 метр. ???? = ????*????2 = 3,14 * 21 * 21 = 1384,74 ≈ 1385 м²
Ответ: 1385 м².
Заключение
В процессе работы над проектом нам удалось отыскать несколько интересных визуализаций, практических ситуаций, в которых необходимо было применить теоретические знания, что позволило мне утверждать, что знания, полученные нами, можно применить на практике даже в ситуациях, от которых зависит исход важного дела.
В работе мы представили как теоретические описание с доказательством отдельных утверждений, так и практические иллюстрации. Доказали длину окружности, площадь круга, показались связь диаметра и длины окружности. Исследовательским компонентом работы стали задачи, которые можно встретить в повседневной жизни на применение изученной теории.
Многообразие форм представления данной теории позволяет лучше усваивать необходимый материал и помогает решать многие геометрические задания с похожим содержанием. Мы показали, что наглядно-образный прием подачи материала на конкретных примерах и ситуациях позволяет усваивать его не только интересней, но и качественней.
Список использованной литературы
1. Атанасян «Геометрия 7-9», Москва, «Просвещение», 1998
2. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбург С. И. Математика, 6 класс. Учебник для учащихся общеобразовательных организаций. М.: Мнемозина, 2014г.
3. Глейзер Г. И. История математики в школе 7-8 кл.: Пособие для учителей. – М.: Просвещение, 1982. С. 32.
4. Гусев В. А. Геометрия 5-6 классы: Учеб. пособие.- М.: ООО «Русское слово», 2002. С.118-142.
5. Епифанов Е. «Портрет» числа π. Коллекция головоломок // Квант, научно - популярный журнал . №4, 2014г.
6. Игнатьев Е. И. «Математическая смекалка». Занимательные задачи, игры, фокусы, парадоксы. Москва, «Омега», 1994.
7. Кессельман B. C. «Занимательная МАТЕМАТИКА» - М.: ACT: Астрель, 2008. — 224 с
8. Колосов Д. Г. Первый шаг в робототехнику. Практикум для 5-6 кл. М.: БИНОМ, Лаборатория знаний, 2015.
9. Панчищина В. А., Гельфман Е. Г. Геометрия, Томск 1999. 10.Перельман Я. И.«Занимательная геометрия», Москва, "Тезис", 1994
10. Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная геометрия: Учеб. пособие для учащихся 5-6 классов. – М.: МИРОС, 1995. С. 72—83.