Файл: Определение длины звуковой волны и скорости звука в воздухе методом резонанса.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 90
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1
Лабораторная работа
Определение длины звуковой волны и скорости звука в воздухе методом резонанса.
Оборудование: звуковой генератор с телефоном, стеклянная трубка с подвижным поршнем, измерительная линейка.
Описание целей работы.
| Описание цели | Критерии достижения цели |
| I. Изучение теории метода
| Студент должен знать определения и приво- дить примеры следующих физических поня- тий и величин:
|
- Определение длины звуковой волны и скорости звука в воздухе методом акустического резонанса.

- Рассчитывать погрешность измерений.
2

-
Основы теории
-
Механические колебания
Механические колебания – это движения, которые точно или приблизитель-
но повторяются через определенные интервалы времени.
Колебания могут быть свободными и вынужденными.
Свободные колебания – колебания, возникающие в системе под действием внутренних сил после того, как система была выведена из положения равновесия. Примеры: колебания груза на пружине или груза, подвешенного на нити. Вынуж- денные колебания – колебания, совершаемые телами под действием каких-то внешних сил. Примеры: поплавок на воде, игла швейной машины, поршни в меха- низмах.
Если колебания повторяются через точные промежутки времени, то такие колебания называются периодическими, а промежуток времени периодом Т (с).
Период Т колебания – минимальный промежуток времени, через который движение тела полностью повторяется. Зная период можно определить частоту ко- лебаний.
Частотой колебаний называется величина
1 , равная числу колебаний,
T
совершающихся за единицу времени. Частота измеряется в герцах ( Гц ): 1 Гц = 1
с –1.
Отклонение точки от положения равновесия называют смещением, а наи- большее отклонение – амплитудой А.
Для описания колебательного движения нужно подобрать функцию перио- дическую и непрерывную. Такими функциями являются функции cos или sin , где = (t) . Наиболее простая зависимость координаты тела от времени при ко- лебательном движении будет иметь вид:
x ( t ) = А cos ( t ) или x ( t ) = A sin ( t ) (1)
Уравнение (1) справедливо, если ось координат ввести вдоль движения ко- леблющейся точки, а за ее начало взять положение равновесия

 Рис.1.
Рис.1.Амплитуда А = | X max |, а смещение = | X |
Аргумент ( t ) в уравнении (1) называют фазой колебаний. Вид функции
(t) : ( t ) = t + 0 (2), где величину 2
T
называют круговой (циклической)
частотой, 0 – начальной фазой.
3
Положение точки при колебательном движении определяется ее фазой:
: t 2 t
T
, где выражение
t показывает, какая доля колебания прошла от начала
T
движения точки, а произведение
мере).
2 tT
переводит эту долю в угол (в радианной
Если реальное колебание совершается в согласии с уравнением (1), то его называют гармоническим. Таким колебанием можно считать колебания матема- тического маятник при малых углах отклонения. Большинство колебаний в приро- де являются негармоническими, но их можно рассматривать как сумму гармониче- ских колебаний.
-
Механические волны.
Волной называют колебания, распространяющиеся в пространстве с течени- ем времени.
Любое реальное тело (твердое, жидкое, газообразное) являет собой множе- ство частиц (молекул , атомов), упруго взаимодействующих между собой. Если любую точку среды вывести из положения равновесия, то она неизбежно вызыва- ет изменение положения окружающих частиц. Если создать колебание одной час- тицы, то в упругой среде колебательные движения передаются от точки к точке.
Существует два типа волн: продольные и поперечные. Волны, у которых частицы среды колеблются в направлении распространения волны, называются продольными волнами. У этих волн чередуются области сгущения и разрежения (рис.2а). Волны, у которой частицы среды колеблются в плоскостях, перпендику- лярных направлению распространения волны, называются поперечными волна- ми. У этих волн происходит чередование горбов и впадин (рис.2б).
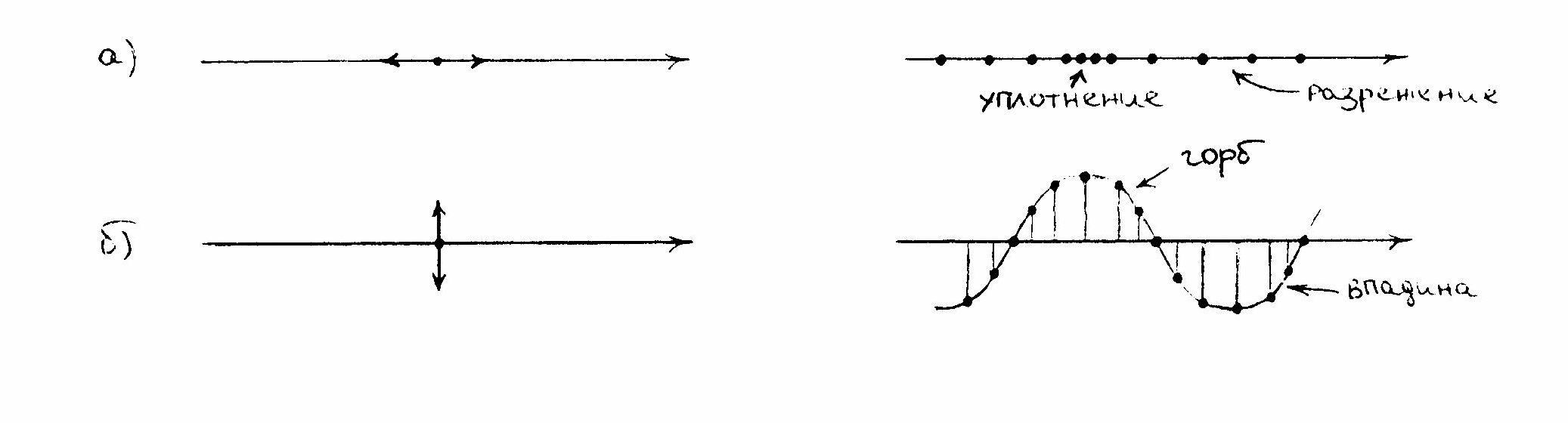
Рис 2. Продольная и поперечная волна.
Таким образом, все точки среды совершают колебания около своих положе- ний равновесия не уходя при этом от своих мест. В простейшем случае все коле- бания можно считать гармоническими, происходящими с одним и тем же перио- дом (частотой), но с различной фазой. Различие фаз связано с тем, что каждая час- тица среды начинает свое колебание только после того, как вступит в движение
4
предыдущая, то есть каждая последующая точка отстает по фазе от предыдущей.
Пусть на рис.3 точками условно изображены частицы линейной упругой среды. Если, например, колебательное движение сообщить первой частице, то ее уравне- ние движения будет иметь вид ( 0 = 0 ): x = A sin t.
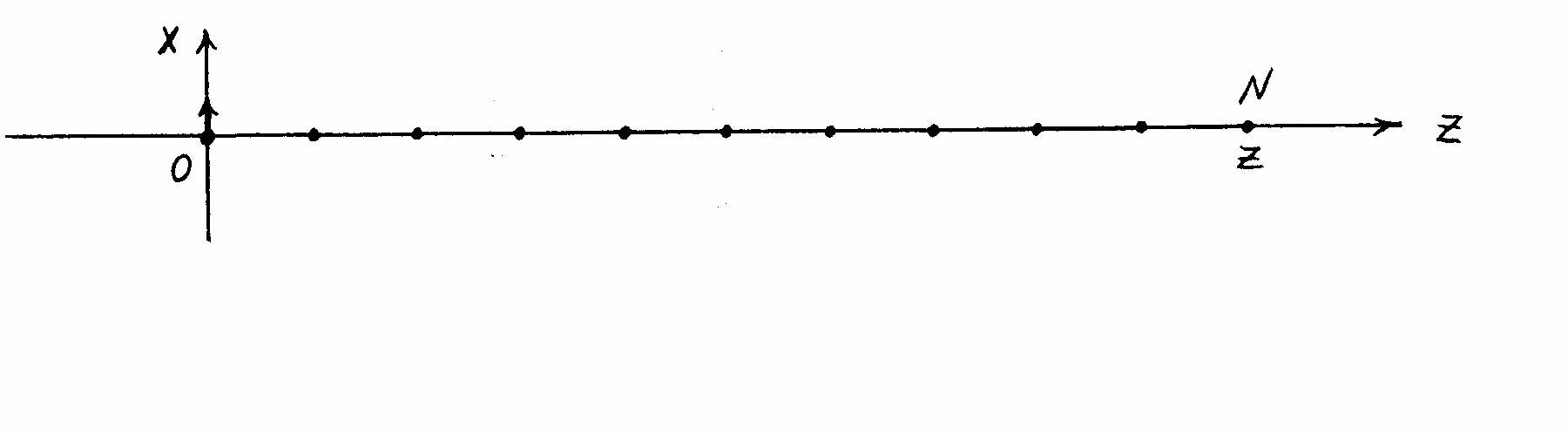
Рис.3. Распространение колебания в упругой среде.
Точка N, отстоящая от первой на расстояние z вдоль направления распро- странения волны, начинает свое движение позже первой точки на промежуток
времени
z, где - скорость, с которой передается (распространяется) колеба-
ние. Тогда уравнение ее движения будет иметь вид:
x= A sin ( t - ) = A sin ( t - z) (3).
Полученное выражение представляет собой уравнение плоской волны, рас- пространяющейся вдоль направления z.
Расстояние, на которое распространяется колебание за один период, называ- ется длиной волны. Оно будет также равно расстоянию между ближайшими час- тицами, колеблющимися в одинаковой фазе
= Т (4),
где - длина волны, - скорость распространения волны, Т – период колебания. Или, учитывая, что Т = 1 / , где - частота колебаний,
= (5)
-
Интерференция волн.
Если в одной и той же среде одновременно распространяются колебания от двух (и более) источников (наложение волн): то каждая волна распространяется независимо друг от друга. Тогда каждая точка (частица) среды должна будет одно- временно совершать два (или более) колебаний, то есть в каждой точке происхо- дит сложение колебаний.
Так как складываемые колебания, происходящие от разных источников волн, могут иметь различные периоды и амплитуды, то результирующее колебание обычно является негармоническим. Интерес представляет случай наложения так называемых когерентных волн.
Когерентными называются волны, разность фаз которых в каждой точке волнового поля постоянна. Такие волны должны не только иметь одинаковую дли-
5
ну волны и частоту, но и излучаться источниками, работающими непрерывно в
течение всего времени наблюдения.
При наложении когерентных волн, в каждой точке поля результирующее колебание будет тоже гармоническим с постоянной амплитудой, причем распре- деление амплитуд в волновом поле будет постоянным.
Если две когерентные волны, бегущие в противоположные стороны, встре- чаются, то при их сложении образуется стоячая волна. Чаще всего, стоячие волны возникают при сложении падающей одномерной волны с волной, испытавшей от- ражение.
При интерференции прямой и отраженной волн возникают участки, где ко- лебательное движение отсутствует (узлы) и участки, где колебания могут происхо- дить с наибольшей амплитудой (пучности).
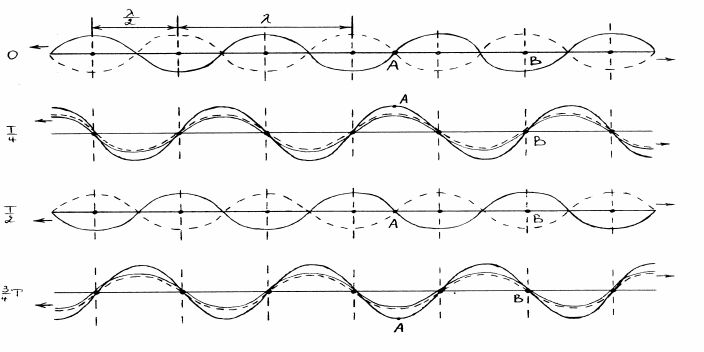
Рис.4. Образование стоячей волны.
На рис.4 пунктирной и сплошной линиями изображены положения двух волн, бегущих навстречу друг другу, через промежутки времени, равные четверти периода. Стрелками указаны направления распространения обеих волн.
За четверть периода каждая из волн перемещается на 1/4. Результирую- щие колебания в каждой точке возникают вследствие сложения двух колебаний.
Рассмотрим движение точки А. На рис.4 при t = 0 обе волны создают в точ- ке А смещение равное нулю. Точка А остается в положении равновесия. Через

6время t = Т / 4 обе волны создают в точке А смещения, направленные в одну сто-
рону, значит смещение точки А от положения равновесия удвоится. При t=3/4T обе волны опять смещают точку А в одном и том же направлении и общее смеще-